DeepFM-Guide

从零开始运行DeepFM项目。

实验准备

安装pycharm

1. 简介
   Jetbrains家族和Pycharm版本划分：
   pycharm是Jetbrains家族中的一个明星产品，Jetbrains开发了许多好用的编辑器，包括Java编辑器（IntelliJ IDEA）、JavaScript编辑器（WebStorm）、PHP编辑器（PHPStorm）、Ruby编辑器（RubyMine）、C和C++编辑器（CLion）、.Net编辑器（Rider）、iOS/macOS编辑器（AppCode）等。pycharm现在在官网[https://www.jetbrains.com/pycharm/download/#section=windows]是分为两个版本，第一个版本是Professional(专业版本)，这个版本功能更加强大，主要是为Python和web开发者而准备，是需要付费的。第二个版本是社区版，一个专业版的阉割版，比较轻量级，主要是为Python和数据专家而准备的。一般我们做开发，下载专业版本比较合适。
2. 下载
   这是 PyCharm 的下载地址：PyCharm下载地址
   进入该网站后，我们会看到如下界面:
   
   professional 表示专业版，community 是社区版，推荐安装专业版，然后通过学生身份免费激活。
   点击Download下载。
3. 安装
   打开下载的安装包，点击Next：
   
   自定义安装路径后，点击Next:
   
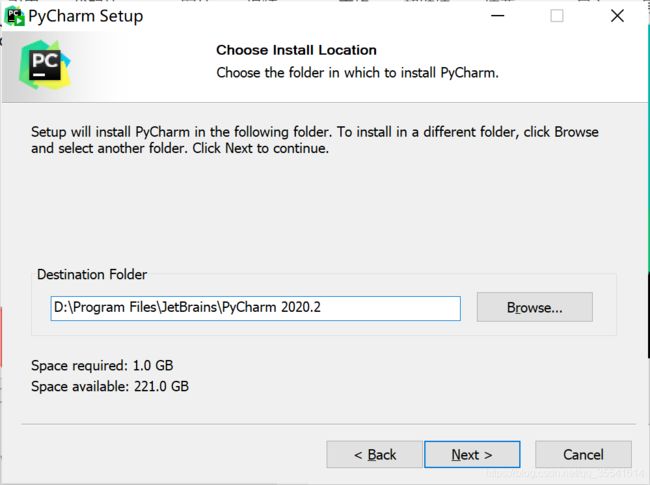
   勾选后，点击Next:
   
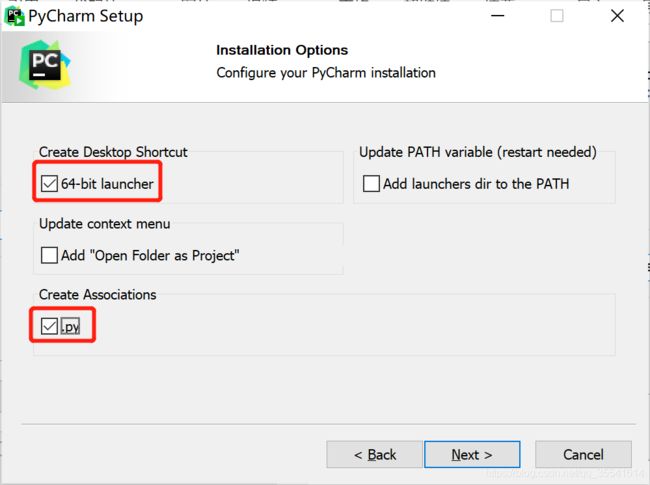
   点击Install进行安装：
   

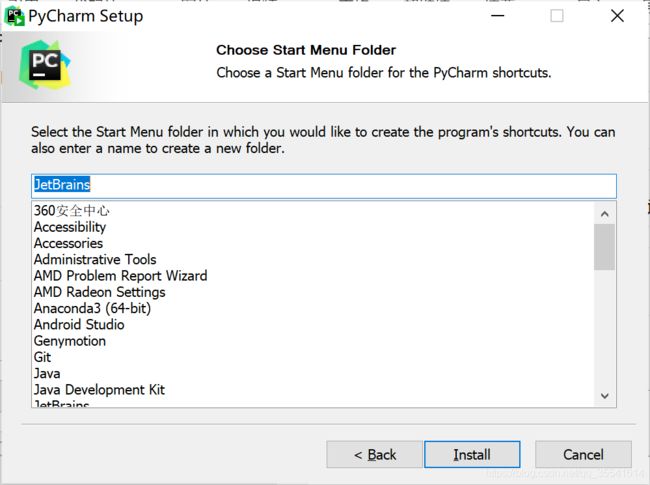
安装python

1. 下载
   进入python官方网站：//www.python.org/
   
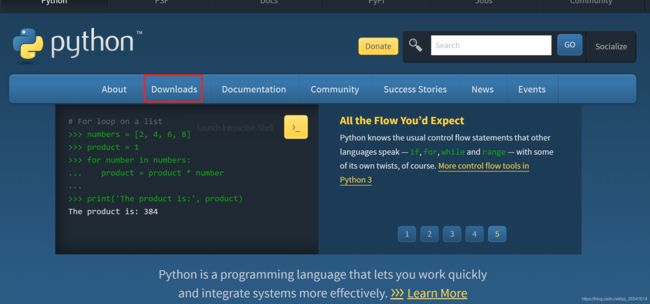
   点击Downloads,进入选择下载界面。
   
   选择3.6.5版本的python，点击Download。
   
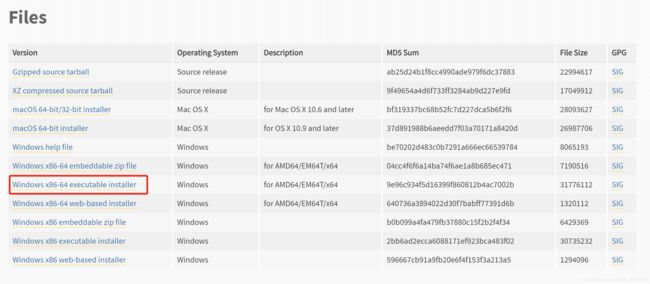
   进入该界面后，点击Windows x86-64 executable installer.因为我们需要用到的是Windows下的解释器，所以在Operating System中可以选择对应的Windows版本，有64位和32位可以选择，我选择的是画红框的这个，executable表示可执行版，需要安装后使用，embeddable表示嵌入版，就是解压以后就可以使用的版本。
   可执行版安装比较简单，一直默认就好了。embeddable需要注意，当我们解压这个文件也是需要解压到同一路径的，这里面放着pip、setuptools等工具，如果不解压，我们将无法在pycharm中更新模块，比如需要用到pymysql，就无法下载。虽然也能用，但是就是"阉割版"的python解释器了。
   如果是embeddable版，记得把解释器所在的路径添加到环境变量里，不然pycharm无法自动获得解释器位置。
2. 安装
   点击下载的安装包，选择Install Now，注意勾选红框中的两个选项，这样就不需要手动添加python的系统环境变量。等待安装完成就好了。
   
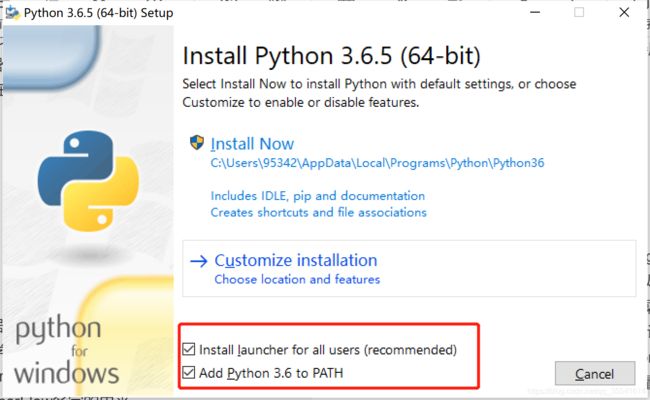
   验证python是否成功安装，代开cmd控制台，输入：

python

出现以下结果，便说明python成功安装，其中，红框标记的是安装的python版本号。

tensorflow基础知识

1.tensorflow简介
TensorFlow是采用数据流图（data　flow　graphs）来计算, 所以首先我们得创建一个数据流流图,然后再将我们的数据（数据以张量(tensor)的形式存在）放在数据流图中计算. 节点（Nodes）在图中表示数学操作,图中的边（edges）则表示在节点间相互联系的多维数据数组, 即张量（tensor).训练模型时tensor会不断的从数据流图中的一个节点flow到另一节点, 这就是TensorFlow名字的由来.
张量（Tensor):张量有多种. 零阶张量为 纯量或标量 (scalar) 也就是一个数值. 比如 [1],一阶张量为 向量 (vector), 比如 一维的 [1, 2, 3],二阶张量为 矩阵 (matrix), 比如 二维的 [[1, 2, 3],[4, 5, 6],[7, 8, 9]],以此类推, 还有 三阶 三维的 …
2.从一个例子讲起
首先，我们来看一个简单的例子：

import tensorflow as tf
import numpy as np
#tensorflow中大部分数据是float32

#create real data
x_data = np.random.rand(100).astype(np.float32)
y_data = x_data * 0.1 + 0.3

### create tensorflow structure start ###

#定义变量
Weights = tf.Variable(tf.random_uniform([1],-1.0,1.0))
biases = tf.Variable(tf.zeros([1]))

#如何计算预测值
y = Weights * x_data + biases

# loss function
loss = tf.reduce_mean(tf.square(y-y_data))

#梯度下降优化器，定义learning rate
optimizer = tf.train.GradientDescentOptimizer(0.5)

#训练目标是loss最小化
train = optimizer.minimize(loss)

#初始化变量，即初始化 Weights 和 biases
init = tf.global_variables_initializer()

#创建session，进行参数初始化
sess = tf.Session()
sess.run(init)

#开始训练200步，每隔20步输出一下两个参数
for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step,sess.run(Weights),sess.run(biases))
### create tensorflow structure end ###

在上面的例子中，我们想要预测的方程式y=0.1*x + 0.3,给定训练样本，通过梯度下降法来预测参数W和偏置b，我们使用numpy生成了我们的训练数据：

x_data = np.random.rand(100).astype(np.float32)
y_data = x_data * 0.1 + 0.3

随后，我们使用tf.Variable定义了我们的变量Weights和biases(以下简称w和b），Weights通过一个均匀分布随机产生，而bias则设置为0，同时二者的形状均为1维，因为只有一个数：

Weights = tf.Variable(tf.random_uniform([1],-1.0,1.0))
biases = tf.Variable(tf.zeros([1]))

好了，有了变量，我们想要学习w和b，只需要用训练数据x来得到预测值，最小化预测值和实际值的差距就好，所以，我们定义了损失函数为平方损失函数，并通过0.5学习率的梯度下降法来进行参数调整：

#如何计算预测值
y = Weights * x_data + biases

# loss function
loss = tf.reduce_mean(tf.square(y-y_data))

#梯度下降优化器，定义learning rate
optimizer = tf.train.GradientDescentOptimizer(0.5)

#训练目标是loss最小化
train = optimizer.minimize(loss)

在tf中定义的变量都需要经过初始化的操作，所以我们定义了一个初始化变量的操作：

#初始化变量，即初始化 Weights 和 biases
init = tf.global_variables_initializer()

接下来我们就可以开始训练了，训练必须创建一个session，通过run方法对指定的节点进行训练，这里一定要注意先要对参数进行初始化，否则后面是无法开始训练的。想要观察训练过程中的参数变化的话，也需要通过run方法：

#创建session，进行参数初始化
sess = tf.Session()
sess.run(init)

#开始训练200步，每隔20步输出一下两个参数
for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step,sess.run(Weights),sess.run(biases))

这里 我们直接run的是train这一步，想要运行这一步，必须先得到optimizier和loss，想要得到loss就要得到预测值…依次往前推，所以run(train)实际上就是对整个tensor流图的训练。
好啦，说了这么多，我们来看一下我们的输出结果吧：

0 [ 0.65090138] [-0.04130311]
20 [ 0.23774943] [ 0.21987261]
40 [ 0.13388598] [ 0.2802889]
60 [ 0.10833587] [ 0.29515111]
80 [ 0.10205062] [ 0.2988072]
100 [ 0.10050445] [ 0.29970658]
120 [ 0.10012411] [ 0.29992783]
140 [ 0.10003054] [ 0.29998225]
160 [ 0.10000751] [ 0.29999563]
180 [ 0.10000186] [ 0.29999894]
200 [ 0.10000047] [ 0.29999974]

可以看到，经过200步，准确的说在80步左右的时候，我们的tensorflow已经能够很准确的将Weights和Bias学习出来了。
3.tf.Session
Session 是 Tensorflow 为了控制,和输出文件的执行的语句. 运行 session.run() 可以获得你要得知的运算结果, 或者是你所要运算的部分，有两种使用Session的方式，我们可以从下面的例子中看出来,但在实际中，我们更推荐后者：

import tensorflow as tf

matrix1 = tf.constant([[3,3]])
matrix2 = tf.constant([[2],[2]])

product = tf.matmul(matrix1,matrix2)

sess = tf.Session()
result = sess.run(product)
print(result)
sess.close()


with tf.Session() as sess:
    result2 = sess.run(product)
    print(result2)

4.tf.Variable
在 Tensorflow 中，定义了某字符串是变量，它才是变量，这一点是与 Python 所不同的。定义语法： state = tf.Variable().如果你在 Tensorflow 中设定了变量，那么初始化变量是最重要的！！所以定义了变量以后, 一定要定义 init = tf.global_variables_initializer().到这里变量还是没有被激活，需要再在 sess 里, sess.run(init) , 激活 init 这一步.

import tensorflow as tf

#定义变量，给定初始值和name
state = tf.Variable(0,name="counter")
#counter:0
print(state.name)

one = tf.constant(1)

new_value = tf.add(state,one)
update = tf.assign(state,new_value)

#这里只是定义，必须用session.run来执行
init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    for _ in range(3):
        sess.run(update)
        print(sess.run(state))

5.TF placeholder
placeholder 是 Tensorflow 中的占位符，暂时储存变量.
Tensorflow 如果想要从外部传入data, 那就需要用到 tf.placeholder(), 然后以这种形式传输数据 sess.run(***, feed_dict={input: **}).

import tensorflow as tf

input1 = tf.placeholder(dtype=tf.float32)
input2 = tf.placeholder(dtype=tf.float32)

output = tf.multiply(input1,input2)

with tf.Session() as sess:
    print(sess.run(output,feed_dict={input1:[3.],input2:[5]}))

FM相关知识

FM相关背景

在计算广告和推荐系统中，CTR预估(click-through rate)是非常重要的一个环节，判断一个商品的是否进行推荐需要根据CTR预估的点击率来进行。在进行CTR预估时，除了单特征外，往往要对特征进行组合。对于特征组合来说，业界现在通用的做法主要有两大类：FM系列与Tree系列。今天，我们就来讲讲FM算法。

one-hot编码带来的问题

FM(Factorization Machine)主要是为了解决数据稀疏的情况下，特征怎样组合的问题。已一个广告分类的问题为例，根据用户与广告位的一些特征，来预测用户是否会点击广告。数据如下：(本例来自美团技术团队分享的paper)

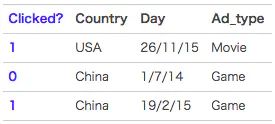
clicked是分类值，表明用户有没有点击该广告。1表示点击，0表示未点击。而country,day,ad_type则是对应的特征。对于这种categorical特征，一般都是进行one-hot编码处理。
将上面的数据进行one-hot编码以后，就变成了下面这样 ：

因为是categorical特征，所以经过one-hot编码以后，不可避免的样本的数据就变得很稀疏。举个非常简单的例子，假设淘宝或者京东上的item为100万，如果对item这个维度进行one-hot编码，光这一个维度数据的稀疏度就是百万分之一。由此可见，数据的稀疏性，是我们在实际应用场景中面临的一个非常常见的挑战与问题。

one-hot编码带来的另一个问题是特征空间变大。同样以上面淘宝上的item为例，将item进行one-hot编码以后，样本空间有一个categorical变为了百万维的数值特征，特征空间一下子暴增一百万。所以大厂动不动上亿维度，就是这么来的。

对特征进行组合

普通的线性模型，我们都是将各个特征独立考虑的，并没有考虑到特征与特征之间的相互关系。但实际上，大量的特征之间是有关联的。最简单的以电商为例，一般女性用户看化妆品服装之类的广告比较多，而男性更青睐各种球类装备。那很明显，女性这个特征与化妆品类服装类商品有很大的关联性，男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来，显然是很有意义的。
一般的线性模型为：

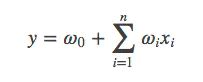
从上面的式子很容易看出，一般的线性模型压根没有考虑特征间的关联。为了表述特征间的相关性，我们采用多项式模型。在多项式模型中，特征xi与xj的组合用xixj表示。为了简单起见，我们讨论二阶多项式模型。具体的模型表达式如下：

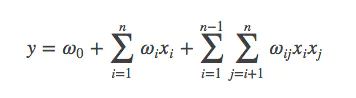
上式中，n表示样本的特征数量,xi表示第i个特征。
与线性模型相比，FM的模型就多了后面特征组合的部分。

FM求解

从上面的式子可以很容易看出，组合部分的特征相关参数共有n(n−1)/2个。但是如第二部分所分析，在数据很稀疏的情况下，满足xi,xj都不为0的情况非常少，这样将导致ωij无法通过训练得出。

为了求出ωij，我们对每一个特征分量xi引入辅助向量Vi=(vi1,vi2,⋯,vik)。然后，利用vivj^T对ωij进行求解。

那么ωij组成的矩阵可以表示为:

那么，如何求解vi和vj呢？主要采用了公式：

具体过程如下：

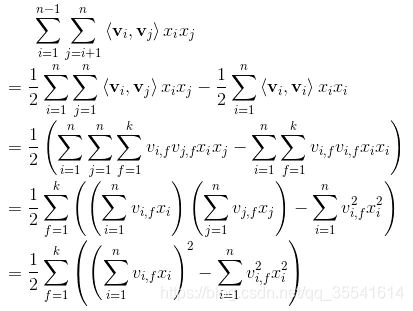
经过这样的分解之后，我们就可以通过随机梯度下降SGD进行求解：

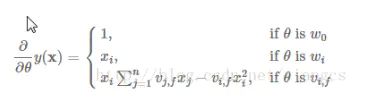
DeepFM相关知识

背景

特征组合的挑战
对于一个基于CTR预估的推荐系统，最重要的是学习到用户点击行为背后隐含的特征组合。在不同的推荐场景中，低阶组合特征或者高阶组合特征可能都会对最终的CTR产生影响。
之前介绍的因子分解机(Factorization Machines, FM)通过对于每一维特征的隐变量内积来提取特征组合。最终的结果也非常好。但是，虽然理论上来讲FM可以对高阶特征组合进行建模，但实际上因为计算复杂度的原因一般都只用到了二阶特征组合。
那么对于高阶的特征组合来说，我们很自然的想法，通过多层的神经网络即DNN去解决。
DNN的局限
下面的图片来自于张俊林教授在AI大会上所使用的PPT。
我们之前也介绍过了，对于离散特征的处理，我们使用的是将特征转换成为one-hot的形式，但是将One-hot类型的特征输入到DNN中，会导致网络参数太多：

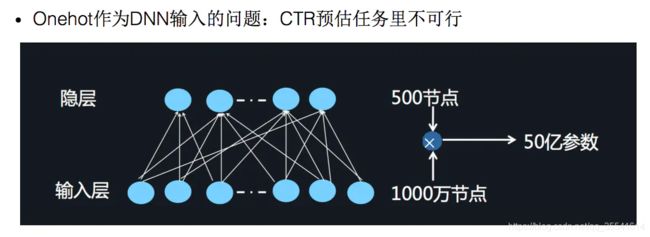
如何解决这个问题呢，类似于FFM中的思想，将特征分为不同的field：

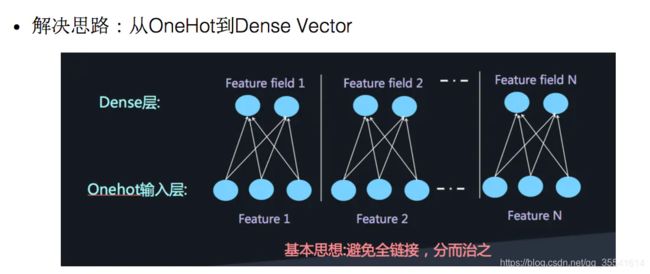
再加两层的全链接层，让Dense Vector进行组合，那么高阶特征的组合就出来了

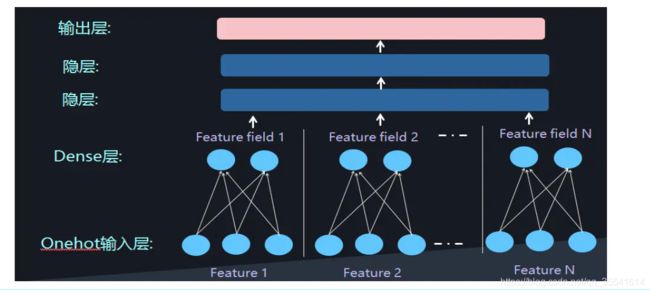
但是低阶和高阶特征组合隐含地体现在隐藏层中，如果我们希望把低阶特征组合单独建模，然后融合高阶特征组合。

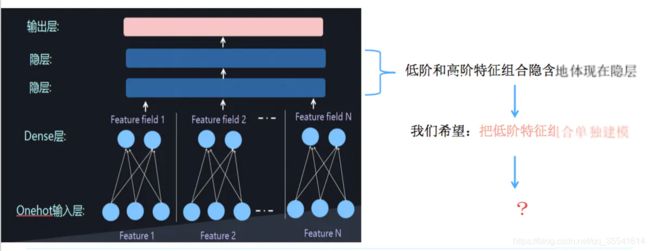
即将DNN与FM进行一个合理的融合：

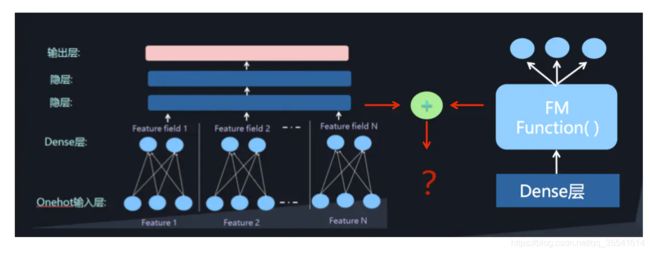
二者的融合总的来说有两种形式，一是串行结构，二是并行结构


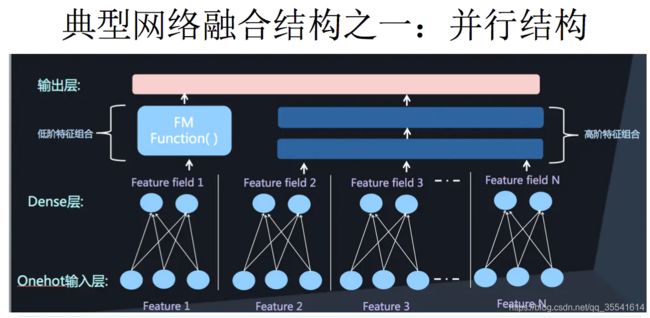
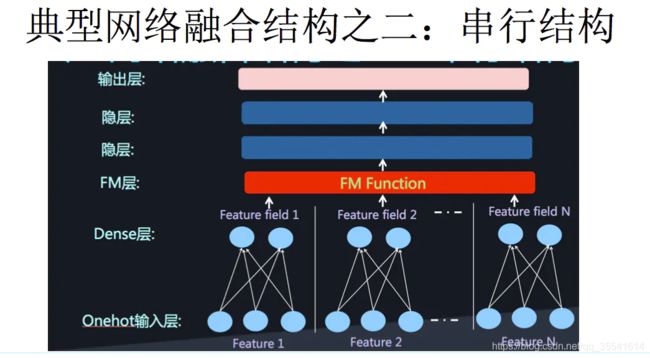
而我们今天要讲到的DeepFM，就是并行结构中的一种典型代表。

DeepFM模型

我们先来看一下DeepFM的模型结构：

DeepFM包含两部分：神经网络部分与因子分解机部分，分别负责低阶特征的提取和高阶特征的提取。这两部分共享同样的输入。DeepFM的预测结果可以写为：

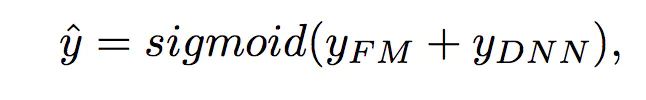
FM部分
FM部分的详细结构如下：

FM部分是一个因子分解机。关于因子分解机可以参阅文章[Rendle, 2010] Steffen Rendle. Factorization machines. In ICDM, 2010.。因为引入了隐变量的原因，对于几乎不出现或者很少出现的隐变量，FM也可以很好的学习。

FM的输出公式为：

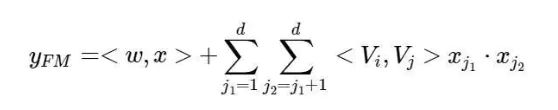
深度部分

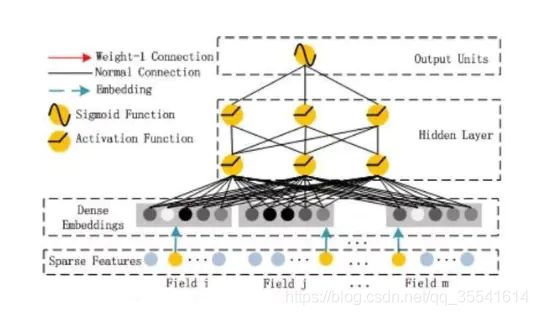
深度部分是一个前馈神经网络。与图像或者语音这类输入不同，图像语音的输入一般是连续而且密集的，然而用于CTR的输入一般是及其稀疏的。因此需要重新设计网络结构。具体实现中为，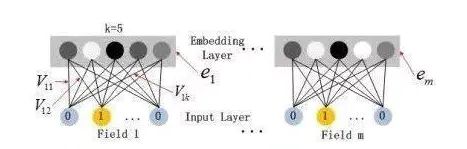
在第一层隐含层之前，引入一个嵌入层来完成将输入向量压缩到低维稠密向量。
嵌入层(embedding layer)的结构如上图所示。当前网络结构有两个有趣的特性，1）尽管不同field的输入长度不同，但是embedding之后向量的长度均为K。2)在FM里得到的隐变量Vik现在作为了嵌入层网络的权重。

这里的第二点如何理解呢，假设我们的k=5，首先，对于输入的一条记录，同一个field 只有一个位置是1，那么在由输入得到dense vector的过程中，输入层只有一个神经元起作用，得到的dense vector其实就是输入层到embedding层该神经元相连的五条线的权重，即vi1，vi2，vi3，vi4，vi5。这五个值组合起来就是我们在FM中所提到的Vi。在FM部分和DNN部分，这一块是共享权重的，对同一个特征来说，得到的Vi是相同的。

有关模型具体如何操作，我们可以通过代码来进一步加深认识。

代码解析

接下来，我们将主要对网络的构建进行介绍，而对数据的处理，流程的控制部分，相信大家根据代码就可以看懂。

项目结构

项目结构如下：
data是用来存放训练数据集。config.py保存了我们模型的一些配置。DataReader对数据进行处理，得到模型可以使用的输入。DeepFM是我们构建的模型。main是项目的入口。metrics是计算normalized gini系数的代码。

模型输入

self.feat_index = tf.placeholder(tf.int32,
                                 shape=[None,None],
                                 name='feat_index')
self.feat_value = tf.placeholder(tf.float32,
                               shape=[None,None],
                               name='feat_value')

self.label = tf.placeholder(tf.float32,shape=[None,1],name='label')
self.dropout_keep_fm = tf.placeholder(tf.float32,shape=[None],name='dropout_keep_fm')
self.dropout_keep_deep = tf.placeholder(tf.float32,shape=[None],name='dropout_deep_deep')

feat_index是特征的一个序号，主要用于通过embedding_lookup选择我们的embedding。feat_value是对应的特征值，如果是离散特征的话，就是1，如果不是离散特征的话，就保留原来的特征值。label是实际值。还定义了两个dropout来防止过拟合。

权重的构建

权重的设定主要有两部分，第一部分是从输入到embedding中的权重，其实也就是我们的dense vector。另一部分就是深度神经网络每一层的权重。第二部分很好理解，我们主要来看看第一部分：

#embeddings
weights['feature_embeddings'] = tf.Variable(
    tf.random_normal([self.feature_size,self.embedding_size],0.0,0.01),
    name='feature_embeddings')
weights['feature_bias'] = tf.Variable(tf.random_normal([self.feature_size,1],0.0,1.0),name='feature_bias')

weights[‘feature_embeddings’] 存放的每一个值其实就是FM中的vik，所以它是F * K的。其中，F代表feture的大小(将离散特征转换成one-hot之后的特征总量),K代表dense vector的大小。

weights[‘feature_bias’]是FM中的一次项的权重。

Embedding part

这个部分比较简单，是根据feat_index选择对应的weights[‘feature_embeddings’]中的embedding值，然后再与对应的feat_value相乘就可以了：

# model
self.embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * K
feat_value = tf.reshape(self.feat_value,shape=[-1,self.field_size,1])
self.embeddings = tf.multiply(self.embeddings,feat_value)

FM part

首先来回顾一下我们之前对FM的化简公式:

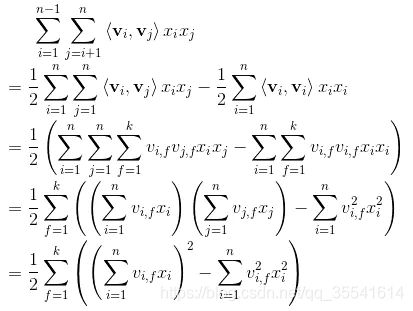
所以我们的二次项可以根据化简公式轻松的得到，再加上我们的一次项，FM的part就算完了。同时更为方便的是，由于权重共享，我们这里可以直接用Embedding part计算出的embeddings来得到我们的二次项：

# first order term
self.y_first_order = tf.nn.embedding_lookup(self.weights['feature_bias'],self.feat_index)
self.y_first_order = tf.reduce_sum(tf.multiply(self.y_first_order,feat_value),2)
self.y_first_order = tf.nn.dropout(self.y_first_order,self.dropout_keep_fm[0])

# second order term
# sum-square-part
self.summed_features_emb = tf.reduce_sum(self.embeddings,1) # None * k
self.summed_features_emb_square = tf.square(self.summed_features_emb) # None * K

# squre-sum-part
self.squared_features_emb = tf.square(self.embeddings)
self.squared_sum_features_emb = tf.reduce_sum(self.squared_features_emb, 1)  # None * K

#second order
self.y_second_order = 0.5 * tf.subtract(self.summed_features_emb_square,self.squared_sum_features_emb)
self.y_second_order = tf.nn.dropout(self.y_second_order,self.dropout_keep_fm[1])

DNN part

DNN part的话，就是将Embedding part的输出再经过几层全链接层：

# Deep component
self.y_deep = tf.reshape(self.embeddings,shape=[-1,self.field_size * self.embedding_size])
self.y_deep = tf.nn.dropout(self.y_deep,self.dropout_keep_deep[0])

for i in range(0,len(self.deep_layers)):
    self.y_deep = tf.add(tf.matmul(self.y_deep,self.weights["layer_%d" %i]), self.weights["bias_%d"%I])
    self.y_deep = self.deep_layers_activation(self.y_deep)
    self.y_deep = tf.nn.dropout(self.y_deep,self.dropout_keep_deep[i+1])

最后，我们要将DNN和FM两部分的输出进行结合：

concat_input = tf.concat([self.y_first_order, self.y_second_order, self.y_deep], axis=1)

损失及优化器

我们可以使用logloss(如果定义为分类问题)，或者mse(如果定义为预测问题)，以及多种的优化器去进行尝试，这些根据不同的参数设定得到：

# loss
if self.loss_type == "logloss":
    self.out = tf.nn.sigmoid(self.out)
    self.loss = tf.losses.log_loss(self.label, self.out)
elif self.loss_type == "mse":
    self.loss = tf.nn.l2_loss(tf.subtract(self.label, self.out))
# l2 regularization on weights
if self.l2_reg > 0:
    self.loss += tf.contrib.layers.l2_regularizer(
        self.l2_reg)(self.weights["concat_projection"])
    if self.use_deep:
        for i in range(len(self.deep_layers)):
            self.loss += tf.contrib.layers.l2_regularizer(
                self.l2_reg)(self.weights["layer_%d" % I])


if self.optimizer_type == "adam":
    self.optimizer = tf.train.AdamOptimizer(learning_rate=self.learning_rate, beta1=0.9, beta2=0.999,
                                            epsilon=1e-8).minimize(self.loss)
elif self.optimizer_type == "adagrad":
    self.optimizer = tf.train.AdagradOptimizer(learning_rate=self.learning_rate,
                                               initial_accumulator_value=1e-8).minimize(self.loss)
elif self.optimizer_type == "gd":
    self.optimizer = tf.train.GradientDescentOptimizer(learning_rate=self.learning_rate).minimize(self.loss)
elif self.optimizer_type == "momentum":
    self.optimizer = tf.train.MomentumOptimizer(learning_rate=self.learning_rate, momentum=0.95).minimize(
        self.loss)

模型效果

前面提到了，我们用logloss作为损失函数去进行模型的参数更新，但是代码中输出了模型的 Normalization 的 Gini值来进行模型评价，我们可以对比一下(记住，Gini值越大越好)：

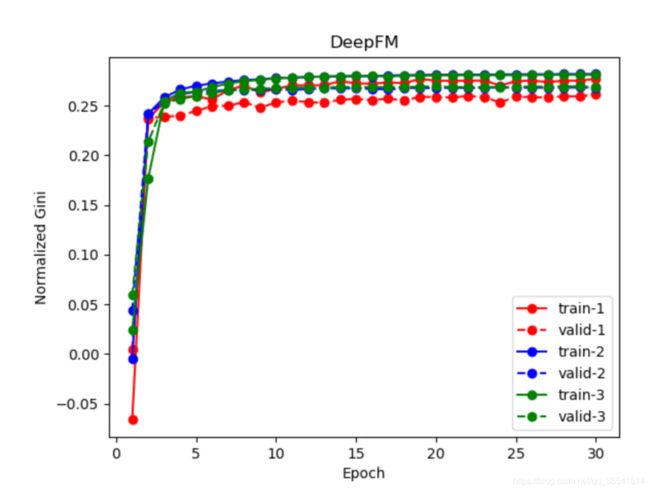
项目运行

从github上下载DeepFM代码，并解压：
github源码地址

1. 打开pycharm，点击Open，选择刚才解压的文件，点击OK。如图所示：
   
   
2. 安装所需要的模块包
   本项目运行需要用到的模块包为：

numpy
pandas
tensorflow
sklearn
matplotlib

其中，tensorflow所需版本为1.14.0
本文将以安装tensorflow为例，告诉大家如何安装所需的python模块。
打开pycharm，点击File->setting

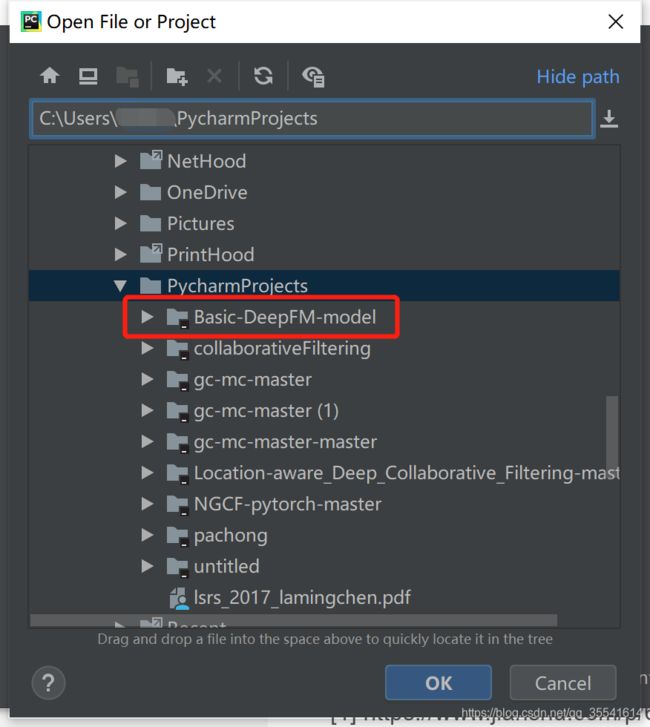
点击Project:Basic-DeepFM-model,点击Project Interpreter，等页面刷新出来后，点击右上方的小加号。

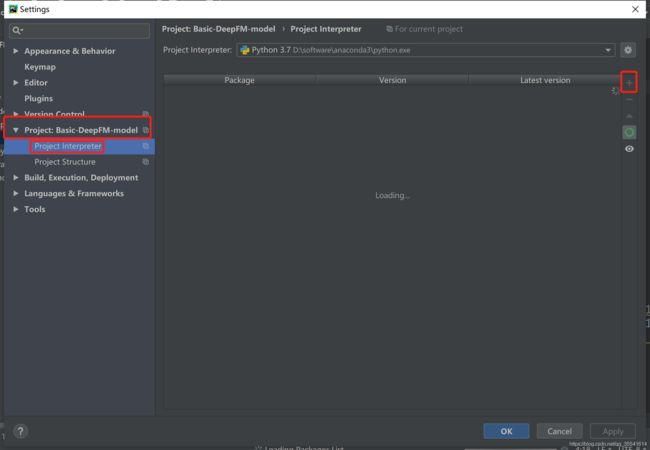
在输入框中，输入“tensorflow”，等待搜索完成，选择搜索结果中出现的tensorflow，然后点击“Install Package”，等待安装完成。

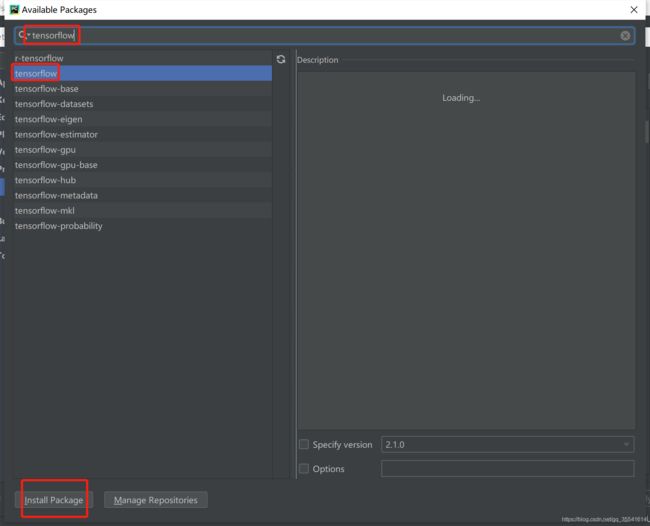
用相同方式安装其他python模块包。
3. 运行项目
待模块包全部安装完成后，右键main.py，选择 Run ‘main’，运行项目，如图所示：

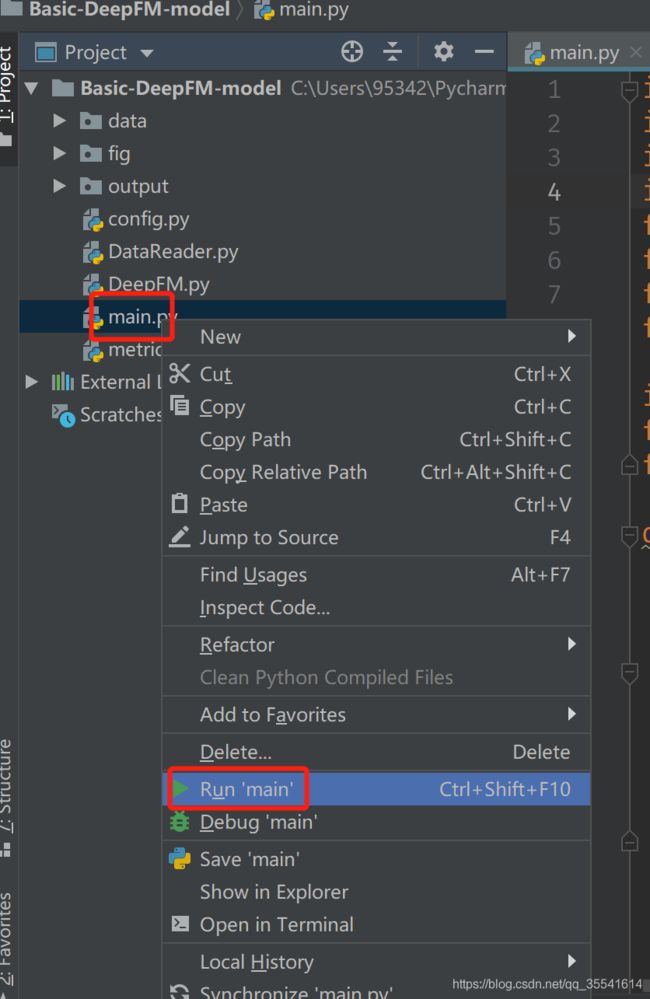
控制台出现如下界面，表示项目运行成功。

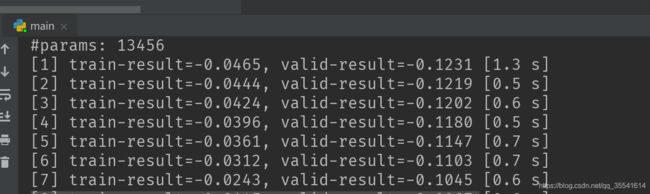
参考

[1] https://www.jianshu.com/p/6f1c2643d31b
[2] https://www.jianshu.com/p/152ae633fb00
[3] https://www.jianshu.com/p/ce213e6b2dc0