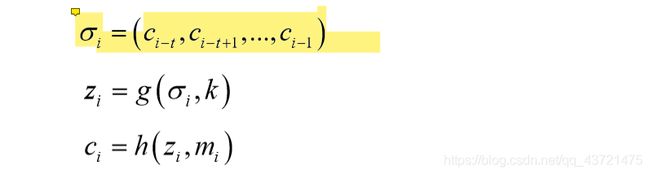流密码(一)同步流密码、自同步流密码以及线性反馈移位寄存器
正式进入密码学领域，发现密码学更像是一门数学，主要是对数论、近世代数的简单应用以及运用在算法中，常常结合模运算以及数字逻辑运算。
流密码的第一部分主要是比较了同步流密码和自同步流密码，其中自同步流密码，由于密钥流的产生与明文有关, 因而较难从理论上进行分析。目前大多 数研究成果都是关于同步流密码的。
至于移位寄存器，是流密码产生密钥流的一个主要组成部分，常用的是线性反馈移位寄存器LFCR。
流密码 （一）
文章目录
- 流密码 （一）
- 流密码分类
- 同步流密码
- 自同步流密码
- 线性反馈移位寄存器LFSR
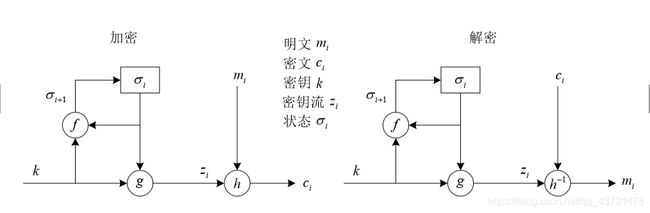
流密码的基本思想是利用密钥 k 产生一个密钥流 z = z0 z1 ⋯,并使用如下规则对明文 串 x = x0 x1 x2 ⋯加密: y = y0 y1 y2 ⋯ = Ez0 ( x0 ) Ez1 ( x1 ) Ez2 ( x2 )⋯。密钥流由密钥流发生 器 f 产生: zi = f( k,σ i ) ,这里σ i 是加密器中的记忆元件(存储器)在时刻 i 的状态, f 是由 密钥 k 和σ i 产生的函数。利用不断变化的加密变换对明文消息进行 逐字符（二进制 ）的加密。流密码的滚动密钥 z0 = f ( k,σ 0 ) 由函数 f、密钥 k 和指定的初态σ 0 完全确定。 0 ) 由函数 f、密钥 k 和指定的初态σ 0 完全确定。此后, 由于输入加密器的明文可能 影响加密器中内部记忆元件的存储状态, 因而σ i ( i > 0)可能依赖于 k,σ 0 , x0 , x1 , ⋯, xi - 1 等参数。
流密码的特点是速度快，且不需很复杂的硬件电路。 仅有有限的差错传播，即某个位符的密码在传输中丢失或出错没有只会对这个位符产生影响。
流密码分类
对称密钥和公开密钥两种
同步和自同步两类 ：根据加密器中记忆元件的存储状态σ i 是否依赖于输入的明文字符, 流密码可进一步 分成同步和自同步两种。σ i 独立于明文字符的叫做同步流密码,否则叫做自同步流密码。
同步流密码
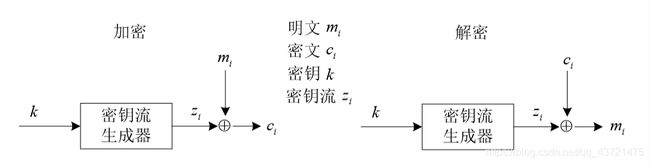
同步流密码指在该密码系统中，密钥流的生成独立明文消息和密文。由于同步流密码的这个特性，可将同步流密码的加密器分成密钥流产生器和加密变换器两个部分
在同步流密码中, 由于 zi = f ( k,σ i )与明文字符无关, 因而此时密文字符 yi = Ezi ( xi )也不依赖于此前的明文字符。的加密变换 Ez i 可以有多种选择, 只要保证变换是可逆的即可。实际使 用的数字保密通信系统一般都是二元系统。
同步流密码的关键是密钥流产生器。一般可将其看成一个参数为 k 的有限状态自动 机, 由一个输出符号集 Z、一个状态集∑、两个函数φ和ψ以及一个初始状态σ 0 。有限状态自助机即能根据有限状态集和输入输出字符集，在转移函数下发生状态转移并形成闭合回路。为了实现这一目标,必须采用非线性函数。
目前最为流行和实用的密钥流产生器驱动部分是一个或多个线性反馈移位寄存器。
同步流密码性质：同步要求严格，需要无错误传播，单个字符的传播错误不影响，但是不能抵御主动攻击。
其中二元加法流密码是一种常见的同步流密码，其中的密钥流、明文及密文字符均为二元字符，并且输出函数h为异或函数。
自同步流密码
自同步流密码（异步流密码）指其中的密钥流是由密钥及固定个数的以前密文字符的函数所生成。 加密过程如图，t为加密寄存器的数量。
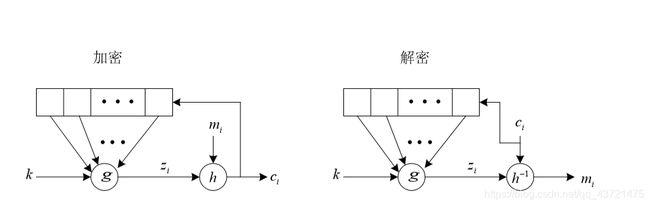性质：自同步，有限的错误传播，传输过程有误会影响t个字符的密码，t为加密解密寄存器中的个数，不能防御主动攻击，攻击者通过攻击打断通信。明文统计扩散，前面的明文密文一直会影响后面的明文密文的产生
线性反馈移位寄存器LFSR
移位寄存器是流密码产生密钥流的一个主要组成部分。其特点：是许多密钥流生成器的基本部件 ；LFSR非常适合硬件的实现 ；可以产生大周期序列 ；可以产生具有良好统计性质的序列 ；易于利用代数方法对其进行分析 。
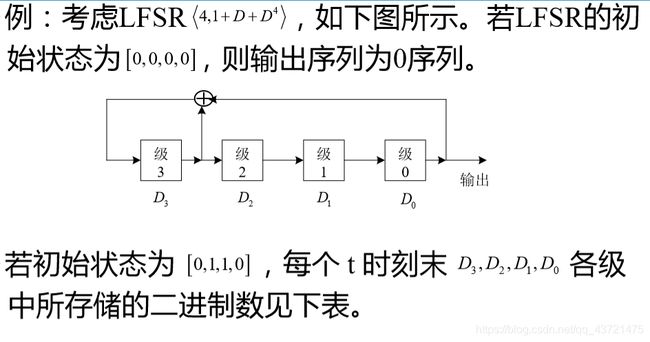
定义：一个长度为L的线性反馈移位寄存器（LFSR ）由0，1，…，L-1共L个级和一个时钟构成，每个级都有1比特输入和1比特输出，并可存储1比特字 符；时钟用于控制数据的移动。每个时间单位内执 行下述操作： 输出0级所存储的字符，以作为输出序列的一部分。 对每个i属于[1,L-1] ,将i级的内容移入i-1级。 L-1级中存储的新元素为反馈比特 sj，它由0，1，…，L-1级中一个固定子集的内容模2相加而得。
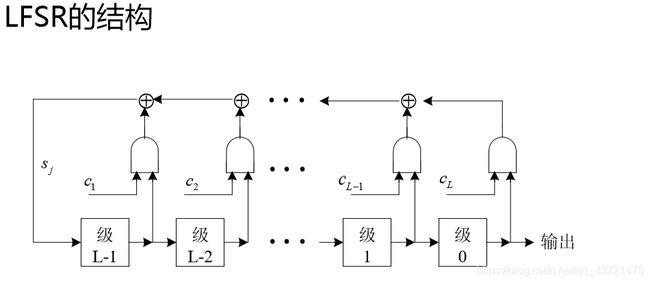上图尤其十分特别重要。其中常数 c i = 0 或 1, 是模 2 加法。 c i = 0 或 1 可用开关的断开和闭合来实现。输出序列{ at }满足an + t = c n at cn - 1 at+ 1 ⋯ c 1 an + t- 1，其中 t 为非负正整数。
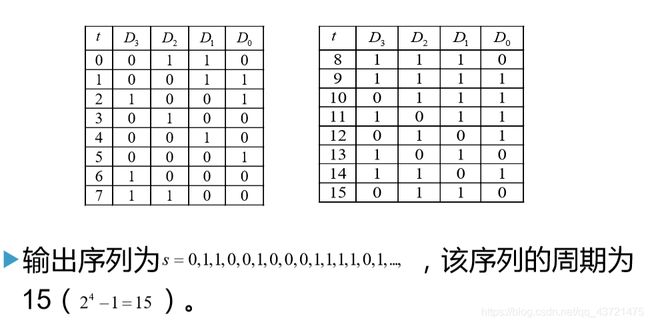
特别注意的是：在线性反馈移位寄存器中总是假定 c 1 , c 2 , ⋯, cn 中至少有一个不为 0, 否则 f ( a1 , a2 ,⋯, an )≡0, 这样的话,在 n 个脉冲后状态必然是 00⋯0。 n 级线性反馈移位寄存器的状态周期小于等于 2n - 1。其 输出序列的周期与状态周期相等, 也小于等于 2n - 1。选择合适的反馈函数便可使 序列的周期达到最大值 2n - 1,周期达到最大值的序列称为 m序列 。
设 n 级线性移位寄存器的输出序列{ ai }满足递推关系
an+ k = c 1 an+ k - 1异或 c 2 an + k - 2 异或⋯ 异或cn ak ( * ) 对任何 k≥1 成立。这种递推关系可用一个一元高次多项式
p( x) = 1 + c 1 x + ⋯ + cn - 1 xn - 1 + cn xn
表示, 称这个多项式为 LFSR 的特征多项式或特征多项式。
看一个例子：
定理 ：n 级 LFSR 产生的序列有最大周期 2^n - 1 的必要条件是其特征多项式为不可约的。
证明 : 设 n级 LFSR 产生的序列周期达到最大 2^n - 1, 除 0 序列外, 每一序列的周期 由特征多项式惟一决定, 而与初始状态无关。设特征多项式为 p( x) , 若 p( x)可约, 可设 为 p( x) = g( x) h( x) , 其中 g( x)不可约, 且次数 k < n。由于 G( g( x)) 属于G( p( x) ) , 而 G( g( x) ) 中序列的周期一方面不超过 2^k - 1 , 另一方面又等于 2^n - 1, 这是矛盾的, 所以 p( x) 不可约。 (证毕)
逆定理不成立f( x) = x^4 + x^3 + x^2 + x + 1 为 GF(2)上的不可约多项式, 这可由 x, x + 1 ,
x^2+x + 1 都不能整除 f ( x)得到。以 f ( x)为特征多项式的 LFSR 的输出序列可由
ak = ak - 1异或 ak - 2 异或ak - 3 异或ak - 4 ( k ≥ 4) 和给定的初始状态求出, 设初始状态为 0001, 则输出序列为 000110001100011⋯, 周期为 5 ,不是 m 序列。
**定理 ** 若 n次不可约多项式 p( x)的阶为 2n - 1 ,则称 p( x)是 n次本原多项式。设{ a i }∈G( p( x)) , { ai }为 m 序列的充要条件是 p( x)为本原多项式。
定义：前图所示LFSR可记为
