强化学习基础 | (14) Actor - Critic
在策略梯度(Policy Gradient)中,我们讲到了基于策略(Policy Based)的强化学习方法的基本思路,并讨论了蒙特卡罗策略梯度reinforce算法。但是由于该算法需要完整的状态序列,同时单独对策略函数进行迭代更新,不太容易收敛。
在本篇我们讨论策略(Policy Based)和价值(Value Based)相结合的方法:Actor-Critic算法。
本文主要参考了Sutton的强化学习书第13章和UCL强化学习讲义的第7讲。
1. Actor-Critic算法简介
Actor-Critic从名字上看包括两部分,演员(Actor)和评价者(Critic)。其中Actor使用我们上一节讲到的策略函数,负责生成动作(Action)并和环境交互。而Critic使用我们之前讲到了的价值函数,负责评估Actor的表现,并指导Actor下一阶段的动作。
回想我们上一篇的策略梯度,策略函数就是我们的Actor,但是那里是没有Critic的,我们当时使用了蒙特卡罗法来计算每一步的价值部分(reward to go)替代了Critic的功能,但是场景比较受限。因此现在我们使用类似DQN中用的价值函数来替代蒙特卡罗法(需要知道完整的状态序列),作为一个比较通用的Critic。
也就是说在Actor-Critic算法中,我们需要做两组近似,第一组是策略函数的近似:
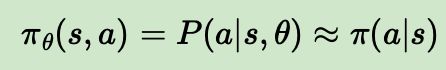
第二组是价值函数的近似,对于状态价值和动作价值函数分别是:

对于我们上一节讲到的蒙特卡罗策略梯度reinforce算法,我们需要进行改造才能变成Actor-Critic算法。
首先,在蒙特卡罗策略梯度reinforce算法中,我们的策略的参数更新公式是:

梯度更新部分中, Δ log π θ ( s t , a t ) \Delta\log_{\pi_{\theta}}(s_t,a_t) Δlogπθ(st,at)是我们的分值函数,不用动,要变成Actor的话改动的是 v t v_t vt,这块不能再使用蒙特卡罗法来得到(reward to go, 需要知道完整的状态序列),而应该从Critic得到。
而对于Critic来说,这块是新的,不过我们完全可以参考之前DQN的做法,即用一个Q网络来做为Critic, 这个Q网络的输入可以是状态,而输出是每个动作的价值或者最优动作的价值。
现在我们汇总来说,就是Critic通过Q网络计算状态的最优价值 v t v_t vt, 而Actor利用 v t v_t vt这个最优价值迭代更新策略函数的参数 θ \theta θ,进而选择动作,并得到反馈和新的状态,Critic使用反馈和新的状态更新Q网络参数w, 在后面Critic会使用新的网络参数w来帮Actor计算状态的最优价值 v t v_t vt。
2. Actor-Critic算法可选形式
在上一节我们已经对Actor-Critic算法的流程做了一个初步的总结,不过有一个可以注意的点就是,我们对于Critic评估的点选择是和上一篇策略梯度一样的状态价值 v t v_t vt,实际上,我们还可以选择很多其他的指标来做为Critic的评估点。而目前可以使用的Actor-Critic评估点主要有:
1)基于状态价值:这是我们上一节使用的评估点,这样Actor的策略函数参数更新的法公式是:
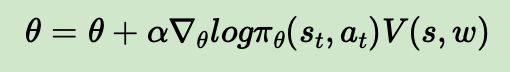
2)基于动作价值:在DQN中,我们一般使用的都是动作价值函数Q来做价值评估,这样Actor的策略函数参数更新的法公式是:

3)基于TD误差:在用时序差分法(TD)求解中,我们讲到了TD误差,它的表达式是 δ ( t ) = R t + 1 + γ V ( S t + 1 ) − V ( S t ) \delta(t) = R_{t+1} + \gamma V(S_{t+1})-V(S_t) δ(t)=Rt+1+γV(St+1)−V(St)或者 δ ( t ) = R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) \delta(t)=R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t) δ(t)=Rt+1+γQ(St+1,At+1)−Q(St,At),这样Actor的策略函数参数更新的法公式是:

4)基于优势函数:在Dueling DQN中,我们讲到过优势函数A的定义: A ( S , A , W , β ) = Q ( S , A , w , α , β ) − V ( S , w , α ) A(S,A,W,\beta)=Q(S,A,w,\alpha,\beta)-V(S,w,\alpha) A(S,A,W,β)=Q(S,A,w,α,β)−V(S,w,α), 即动作价值函数和状态价值函数的差值。这样Actor的策略函数参数更新的法公式是:

5)基于 T D ( λ ) TD(\lambda) TD(λ)误差:一般都是基于后向 T D ( λ ) TD(\lambda) TD(λ)误差, 在用时序差分法(TD)求解中也有讲到,是TD误差和效用迹E的乘积。这样Actor的策略函数参数更新的法公式是:
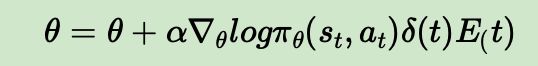
对于Critic本身的模型参数w,一般都是使用均方误差损失函数来做迭代更新,类似之前DQN系列中所讲的迭代方法. 如果我们使用的是最简单的线性Q函数,比如 Q ( s , a , w ) = ϕ ( s , a ) T w Q(s,a,w)=\phi(s,a)^Tw Q(s,a,w)=ϕ(s,a)Tw, 则Critic本身的模型参数w的更新公式可以表示为:
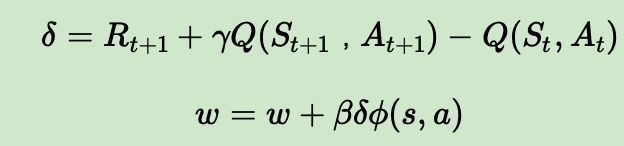
通过对均方误差损失函数求导可以很容易的得到上式。当然实际应用中,我们一般不使用线性Q函数,而使用神经网络表示状态和Q值的关系。
3. Actor-Critic算法流程
这里给一个Actor-Critic算法的流程总结,评估点基于TD误差,Critic使用神经网络来计算TD误差并更新网络参数,Actor也使用神经网络来更新网络参数。
算法输入:迭代轮数T,状态特征维度n, 动作集A, 步长 α , β \alpha,\beta α,β,衰减因子 γ \gamma γ, 探索率 ϵ \epsilon ϵ, Critic网络结构和Actor网络结构。
输出:Actor 网络参数 θ \theta θ, Critic网络参数w
1)随机初始化所有的状态和动作对应的价值Q
2)for i from 1 to T,进行迭代。
a)初始化S为当前状态序列的第一个状态, 拿到其特征向量 ϕ ( S ) \phi(S) ϕ(S)
b)在Actor网络中使用 ϕ ( S ) \phi(S) ϕ(S)作为输入,输出动作A,基于动作A得到新的状态S’以及反馈R
c)在Critic网络中分别使用 ϕ ( S ) , ϕ ( S ′ ) \phi(S),\phi(S') ϕ(S),ϕ(S′), 得到Q值输出V(S), V(S’)
d)计算TD误差 δ = R + γ V ( S ′ ) − V ( S ) \delta = R+\gamma V(S') - V(S) δ=R+γV(S′)−V(S)
e)使用均方误差损失函数 ∑ ( R + γ V ( S ′ ) − V ( S ) ) 2 \sum(R+\gamma V(S') - V(S))^2 ∑(R+γV(S′)−V(S))2对Critic网络参数w做梯度更新
f)更新Actor网络参数 θ \theta θ:

对于Actor的分值函数 Δ θ log π θ ( S t , A t ) \Delta_{\theta}\log_{\pi_{\theta}}(S_t,A_t) Δθlogπθ(St,At),可以选择softmax或者高斯分值函数。
上述Actor-Critic算法已经是一个很好的算法框架,但是离实际应用还比较远。主要原因是这里有两个神经网络,都需要梯度更新,而且互相依赖。但是了解这个算法过程后,其他基于Actor-Critic的(改进)算法就好理解了。
4. Actor-Critic算法实例
下面我们用一个具体的例子来演示上面的Actor-Critic算法。仍然使用了OpenAI Gym中的CartPole-v0游戏来作为我们算法应用。CartPole-v0游戏的介绍参见这里。它比较简单,基本要求就是控制下面的cart移动使连接在上面的pole保持垂直不倒。这个任务只有两个离散动作,要么向左用力,要么向右用力。而state状态就是这个cart的位置和速度, pole的角度和角速度,4维的特征。坚持到200分的奖励则为过关。
算法流程可以参考上面的第三节,这里的分值函数我们使用的是softmax函数,和上一篇的类似。完整代码
代码主要分为两部分,第一部分是Actor,第二部分是Critic。对于Actor部分,大家可以和上一篇策略梯度的代码对比,改动并不大,主要区别在于梯度更新部分,策略梯度使用是蒙特卡罗法计算出的价值 v t v_t vt,则我们的actor使用的是TD误差。
在策略梯度部分,对应的位置如下
self.loss = tf.reduce_mean(self.neg_log_prob * self.tf_vt) # reward guided loss
而我们的Actor对应的位置的代码是:
self.exp = tf.reduce_mean(self.neg_log_prob * self.td_error)
此处要注意的是,由于使用的是TD误差,而不是价值v(t),此处需要最大化self.exp,而不是最小化它,这点和策略梯度不同。对应的Actor代码为:
#这里需要最大化当前策略的价值,因此需要最大化self.exp,即最小化-self.exp
self.train_op = tf.train.AdamOptimizer(LEARNING_RATE).minimize(-self.exp)
除此之外,Actor部分的代码和策略梯度的代码区别并不大。
对于Critic部分,我们使用了类似于DQN的三层神经网络。不过我们简化了这个网络的输出,只有一维输出值,而不是之前DQN使用的有多少个可选动作,就有多少维输出值。网络结构如下:
def create_Q_network(self):
# network weights
W1q = self.weight_variable([self.state_dim, 20])
b1q = self.bias_variable([20])
W2q = self.weight_variable([20, 1])
b2q = self.bias_variable([1])
self.state_input = tf.placeholder(tf.float32, [1, self.state_dim], "state")
# hidden layers
h_layerq = tf.nn.relu(tf.matmul(self.state_input, W1q) + b1q)
# Q Value layer
self.Q_value = tf.matmul(h_layerq, W2q) + b2q
和之前的DQN相比,这里还有一个区别就是我们的critic没有使用DQN的经验回放,只是使用了反馈和当前网络在下一个状态的输出来拟合当前状态。
对于算法中Actor和Critic交互的逻辑,在main函数中:
for step in range(STEP):
action = actor.choose_action(state) # e-greedy action for train
next_state,reward,done,_ = env.step(action)
td_error = critic.train_Q_network(state, reward, next_state) # gradient = grad[r + gamma * V(s_) - V(s)]
actor.learn(state, action, td_error) # true_gradient = grad[logPi(s,a) * td_error]
state = next_state
if done:
break
大家对照第三节的算法流程和代码应该可以比较容易理清这个过程。但是这个程序很难收敛。因此大家跑了后发现分数总是很低的话是可以理解的。我们需要优化这个问题。
5. Actor-Critic算法小结
基本版的Actor-Critic算法虽然思路很好,但是由于难收敛的原因,还需要做改进。
目前改进的比较好的有两个经典算法,一个是DDPG算法,使用了双Actor神经网络和双Critic神经网络的方法来改善收敛性。这个方法我们在从DQN到Nature DQN的过程中已经用过一次了。另一个是A3C算法,使用了多线程的方式,一个主线程负责更新Actor和Critic的参数,多个辅线程负责分别和环境交互,得到梯度更新值,汇总更新主线程的参数。而所有的辅线程会定期从主线程更新网络参数。这些辅线程起到了类似DQN中经验回放的作用,但是效果更好。