最小二乘法拟合椭圆——MATLAB和Qt-C++实现

本小节Jungle尝试用最小二乘法拟合椭圆，并用MATLAB和C++实现。

1.理论知识

平面上任意位置的一个椭圆，其中心坐标为（x0，y0），半长轴a，半短轴b，长轴偏角为θ，方程通式为

其中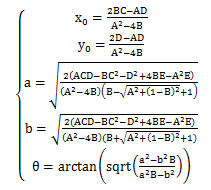
在原始测得的N（N≥5）组数据（xi，yi），（i=1,2,3,…,N）中，根据椭圆方程通式和最小二乘法原理，求目标函数

的最小值来确定参数A、B、C、D和E。令F（A，B，C，D，E）对各个参数的偏导数均为零，得到以下方程组：

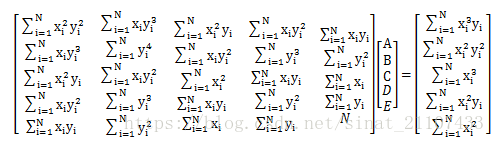
求解此线性方程组可解出A、B、C、D和E，代入第二个方程即可解得拟合的椭圆的参数。

2.MATLAB实现

function [ p ] = Ellipse_FittingLS( XY )
N = size(XY,1);
x = XY(:,1);
y = XY(:,2);

sum_X2Y2=0;
sum_X1Y3=0;
sum_X2Y1=0;
sum_X1Y2=0;
sum_X1Y1=0;
sum_Y4=0;
sum_Y3=0;
sum_Y2=0;
sum_X2=0;
sum_X1=0;
sum_Y1=0;
sum_X3Y1=0;
sum_X3=0;

for i = 1:N
    sum_X2Y2 = sum_X2Y2+x(i)*x(i)*y(i)*y(i);
    sum_X1Y3 = sum_X1Y3+x(i)*y(i)*y(i)*y(i);
    sum_X2Y1 = sum_X2Y1+x(i)*x(i)*y(i);
    sum_X1Y2 = sum_X1Y2+x(i)*y(i)*y(i);
    sum_X1Y1 = sum_X1Y1+x(i)*y(i);
    sum_Y4 = sum_Y4+y(i)*y(i)*y(i)*y(i);
    sum_Y3 = sum_Y3+y(i)*y(i)*y(i);
    sum_Y2 = sum_Y2+y(i)*y(i);
    sum_X2 = sum_X2+x(i)*x(i);
    sum_X1 = sum_X1+x(i);
    sum_Y1 = sum_Y1+y(i);
    sum_X3Y1 = sum_X3Y1+x(i)*x(i)*x(i)*y(i);
    sum_X3 = sum_X3+x(i)*x(i)*x(i);
end

M1 = [sum_X2Y2,sum_X1Y3,sum_X2Y1,sum_X1Y2,sum_X1Y1;
     sum_X1Y3,sum_Y4,sum_X1Y2,sum_Y3,sum_Y2;
     sum_X2Y1,sum_X1Y2,sum_X2,sum_X1Y1,sum_X1;
     sum_X1Y2,sum_Y3,sum_X1Y1,sum_Y2,sum_Y1;
     sum_X1Y1,sum_Y2,sum_X1,sum_Y1,N
    ];
M2 = [sum_X3Y1;sum_X2Y2;sum_X3;sum_X2Y1;sum_X2];
M3 = inv(M1);
M4 = M3*M2;
A = M4(1);
B = M4(2);
C = M4(3);
D = M4(4);
E = M4(5);

Xc = (2*B*C-A*D)/(A*A-4*B);
Yc = (2*D-A*D)/(A*A-4*B);
a = sqrt(abs(2*(A*C*D-B*C*C-D*D+4*B*E-A*A*E)/((A*A-4*B)*(B-sqrt(A*A+(1-B)*(1-B))+1))));
b = sqrt(abs(2*(A*C*D-B*C*C-D*D+4*B*E-A*A*E)/((A*A-4*B)*(B+sqrt(A*A+(1-B)*(1-B))+1))));
theta = atan(sqrt(abs((a*a-b*b*B)/(a*a*B-b*b))));
p = [Xc,Yc,a,b,theta];
end

3.C++和Qt实现

Jungle将拟合椭圆的方法及椭圆相关参数封装到一个类EllipseFitting中。类中用到了Qt自带的数据结构QList，也可以用数组或者STL中的数据结构，如vetor等。

#ifndef ELLIPSEFITTING_H
#define ELLIPSEFITTING_H

#include 
#include 
#include 
#include "math.h"

class EllipseFitting
{
public:
	EllipseFitting(QList);
	~EllipseFitting();

	///拟合椭圆
	void fittingData();
	///返回拟合结果
	QList getResultList();

private:

	///原始数据集合
	QList PrimiDataSet;
	///拟合结果列表
	QListresultList;
	///拟合椭圆的重要参数：椭圆中心坐标（Xc,Yc),长半轴a，短半轴b,偏移角theta
	double Xc;
	double Yc;
	double a;
	double b;
	double theta;
};

#endif // ELLIPSEFITTING_H

实现

#include "ellipsefitting.h"
#define n 5

EllipseFitting::EllipseFitting(QList idataset)
{
	this->Xc = 0.00;
	this->Yc = 0.00;
	this->a = 0.00;
	this->b = 0.00;
	this->theta = 0.00;
	this->resultList.clear();
	for(int i=0;iPrimiDataSet<fittingData();
}

EllipseFitting::~EllipseFitting()
{
	
}

QList EllipseFitting::getResultList()
{
	return this->resultList;
}

void EllipseFitting::fittingData()
{
	long double A = 0.00,B = 0.00,C = 0.00,D = 0.00,E = 0.00;
	long double x2y2=0.0,x1y3=0.0,x2y1=0.0,x1y2=0.0,x1y1=0.0,yyy4=0.0,yyy3=0.0,yyy2=0.0,xxx2=0.0,xxx1=0.0,yyy1=0.0,x3y1=0.0,xxx3=0.0;
	int N = PrimiDataSet.size();
	for(int i = 0; i < PrimiDataSet.size(); i++)
	{
		long double xi = PrimiDataSet[i]->x, yi = PrimiDataSet[i]->y;

		x2y2 += xi*xi*yi*yi;
		x1y3 += xi*yi*yi*yi;
		x2y1 += xi*xi*yi;
		x1y2 += xi*yi*yi;
		x1y1 += xi*yi;
		yyy4 += yi*yi*yi*yi;
		yyy3 += yi*yi*yi;
		yyy2 += yi*yi;
		xxx2 += xi*xi;
		xxx1 += xi;
		yyy1 += yi;
		x3y1 += xi*xi*xi*yi;
		xxx3 += xi*xi*xi;
	}
	long double matrix[5][5]={{x2y2,x1y3,x2y1,x1y2,x1y1},
							  {x1y3,yyy4,x1y2,yyy3,yyy2},
						      {x2y1,x1y2,xxx2,x1y1,xxx1},
							  {x1y2,yyy3,x1y1,yyy2,yyy1},
							  {x1y1,yyy2,xxx1,yyy1,N}
							 };

	long double matrix2[5][1]={x3y1,x2y2,xxx3,x2y1,xxx2};
	long double matrix3[5][1] = {A,B,C,D,E};

	求矩阵matrix的逆，结果为InverseMatrix
	///单位矩阵
	long double E_Matrix[n][n];
	long double mik;
	long double m = 2*n;
	for(int i = 0; i < n; i++)
	{
		for(int j = 0; j < n; j++)
		{
			if(i == j)
				E_Matrix[i][j] = 1.00;
			else
				E_Matrix[i][j] = 0.00;
		}
	}
	long double CalcuMatrix[n][2*n];
	for(int i = 0; i < n; i++)
	{
		for(int j = 0; j < n; j++)
		{
			CalcuMatrix[i][j] = matrix[i][j];
		}
		for(int k = n; k < m; k++)
		{
			CalcuMatrix[i][k] = E_Matrix[i][k-n];
		}
	}

	for(int i = 1; i <= n-1; i++)
	{
		for(int j = i+1; j <= n; j++)
		{
			mik = CalcuMatrix[j-1][i-1]/CalcuMatrix[i-1][i-1];
			for(int k = i+1;k <= m; k++)
			{
				CalcuMatrix[j-1][k-1] -= mik*CalcuMatrix[i-1][k-1];
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		long double temp = CalcuMatrix[i-1][i-1];
		for(int j=1;j<=m;j++)
		{
			CalcuMatrix[i-1][j-1] = CalcuMatrix[i-1][j-1]/temp;
		}
	}
	for(int k=n-1;k>=1;k--)
	{
		for(int i=k;i>=1;i--)
		{
			mik = CalcuMatrix[i-1][k];
			for(int j=k+1;j<=m;j++)
			{
				CalcuMatrix[i-1][j-1] -= mik*CalcuMatrix[k][j-1];
			}
		}
	}
	long double InverseMatrix[n][n];
	for(int i=0;i