python 数据结构之排序

冒泡排序法：
冒泡排序其时间复杂度为O（n^2），它是一个两两比较的过程，将第i个元素与剩下从i+1开始到结尾的元素逐个比较实现排序的
例如以下表格（冒泡排序）

5	2	7	3

首先将5与2比较，5>2 交换

2	5	7	3

再将5与7对比，5<7，不动
再将7与3对比，7>3，交换

2	5	3	7

这样一轮循环就结束了，也就是将最大的放到了末尾，以此类推，将次大的放到倒数第二个…
代码：

def bubbleSort(alist):
    for i in range(len(alist)-1,0,-1):
        for j in range(i):
            if alist[i] < alist[j]:
                alist[i],alist[j] = alist[j],alist[i]  #python支持直接交换
    return alist

testlist = [3,5,4,2,7,6,9]
print(bubbleSort(testlist))

选择排序在之前已经写过了，它的时间复杂度和冒泡排序是一样的，因为其基本原理差不多，只是它一次循环只做一次交换，所以选择排序较冒泡排序较优。
插入排序：
插入排序的算法复杂度任然为O（n^2），但是算法思想与上面两个截然不同，它相当于插扑克牌一样，首先选取首元素（或尾元素）为子列表，然后将剩下的元素逐个插入到子列表中（相当于子列表每次扩充一个元素）最后得到排好序的列表

5	2	7	3

选取5为子列表（即zilist = 【5】）
首先插入2（插在5前面，zilist = 【2，5】）
在插入7（zilist = 【2，5，7】）
最后插入3（zilist = 【2，3，5，7】）
插入排序算法图例：

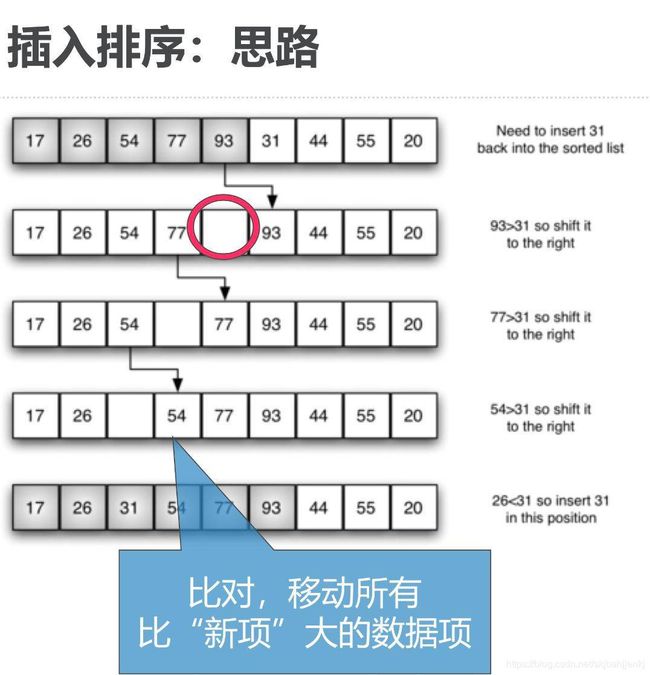
代码：

def insertionSort(alist):
    for index in range(1,len(alist)):
        currentvaule = alist[index]
        position = index
        while currentvaule < alist[position - 1] and position > 0:
            alist[position] = alist[position - 1]
            position = position - 1
        alist[position] = currentvaule
    return alist

testlist = [2,5,3,9,6,7,1]
print(insertionSort(testlist))

谢尔排序：
间隔是3的子序列：
排序之前：2,6,3,9,5,7,1
排序之后：1,6,3,2,5,7,9
排序之前：1,6,3,2,5,7,9
排序之后：1,5,3,2,6,7,9
排序之前：1,5,3,2,6,7,9
排序之后：1,5,3,2,6,7,9
间隔是1的子序列：
相当于进行一次插入排序
排序之前：1,5,3,2,6,7,9
排序之后：1,2,3,5,6,7,9
子列表的间隔一般上一次间隔的1/2，直到为1
粗看上去，谢尔排序中含有插入排序，可能并不会比插入排序好，但是由于每一趟排序所构成的子序列都会使得列表离顺序表更进一步，所以最后一趟插入排序会减少许多原来需要进行的无效比对
谢尔排序的时间复杂度在O（n)与O（n^2）之间

def shellSort(alist):
    interval = len(alist) // 2  #设定间隔
    while interval >= 1:
        for startposition in range(interval):
            gapInsertionSort(alist,startposition,interval)  #调用函数排序
        interval = interval // 2  #缩小间隔
    return alist
def gapInsertionSort(alist,start,gap):  #插入排序函数
    for i in range(start + gap,len(alist),gap):
        currentvalue = alist[i]
        position = i
        while position >= gap and alist[position - gap] > currentvalue:
            alist[position] = alist[position - gap]
            position = position - gap
        alist[position] = currentvalue
    return alist
testlist = [3,2,5,9,1,4,6,0]
print(shellSort(testlist))

归并排序：
归并排序是递归算法，其主要分为两部分：分裂，归并。分裂过程类比与二分法查找，时间复杂度为O（log n），归并过程相对于分裂的每个部分，其所以数据项都会被比较和放置一次，所以其时间复杂度为O（n）。综合考虑，每次分裂的部分都进行一次O（n）的数据归并，总的时间复杂度为O（nlog n）。
算法图示如下：

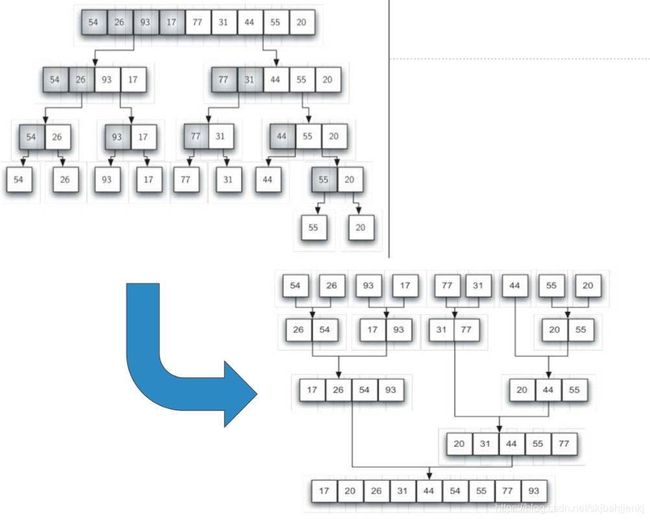
def mergeSort(alist):
    if len(alist) > 1:  #递归基本结束条件
        alist1 = alist[:len(alist) // 2]
        alist2 = alist[len(alist) // 2:]
        mergeSort(alist1)
        mergeSort(alist2) #上半部分是分裂过程
        length = i = j =0
        while (i < len(alist1)) and (j < len(alist2)):  #开始归并拉链式交错对比大小
            if alist1[i] < alist2[j]:
                alist[length] = alist1[i]
                i = i + 1
            else:
                alist[length] = alist2[j]
                j = j + 1
            length = length + 1
        while j < len(alist2):  #归并左半部分剩余项
            alist[length] = alist2[j]
            j = j + 1
            length = length + 1
        while i < len(alist1):  #归并右半部分剩余项
            alist[length] = alist1[i]
            i = i + 1
            length = length + 1
    return alist

testlist = [2,5,9,7,1,4,6,3]
print(mergeSort(testlist))

我们需要注意的是归并排序算法使用了额外一倍的存储空间用于归并，下面介绍一个python风格的代码：

def mergeSort(alist):
    if len(alist) <= 1:  #递归基本结束条件
        return alist
    mid = len(alist) // 2
    left = mergeSort(alist[:mid])
    right = mergeSort(alist[mid:])
    merged = []
    while right and left:
        if left[0] <= right[0]:
            merged.append(left.pop(0))
        else:
            merged.append(right.pop(0))
    merged.extend(right if right else left)
    return merged

testlist = [2,5,9,7,1,4,6,3]
print(mergeSort(testlist))

其基本思路与上面的相同
快速排序：
快速排序依旧是递归思想，其思路是依据一个“中值”（中值可以是依据算法找到中位数，也可以是任意取一个数）将数据分成两半：大于中值的一半和小于中值的一半，然后对两边分别在取一个中值，以此类推。
例如下图中进行了一次排序找到了第一个中值54：

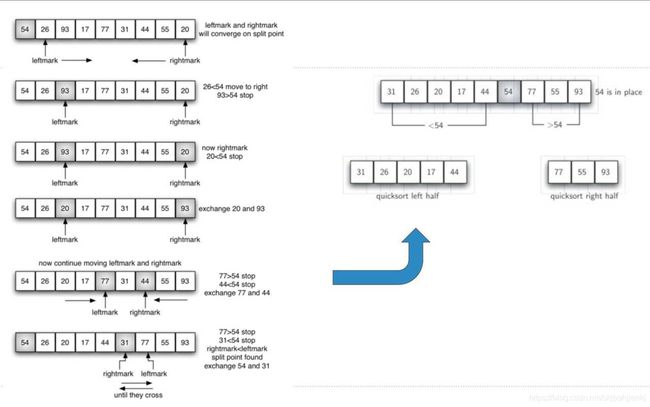
快速排序代码：

def quickSort(alist):
    quickSortHelp(alist,0,len(alist) - 1)
    return alist
def quickSortHelp(alist,first,last):
    if first < last :
        mid_value = partition(alist,first,last)
        quickSortHelp(alist,first,mid_value-1)
        quickSortHelp(alist,mid_value+1,last)

def partition(alist,left,right):
    mid_value = alist[left]
    first,last = left + 1,right
    while first <= last:
        if alist[first] < mid_value:
            first = first + 1
        else:
            if alist[last] > mid_value:
                last = last - 1
            else:
                alist[first],alist[last] = alist[last],alist[first]
    alist[left],alist[last] = alist[last],alist[left]
    return mid_value

testlist = [2,4,3,7,1,5,9,6]
print(quickSort(testlist))

上面是几个基本排序的算法思想，其实在我们使用python时，一般都会使用python的内置排序函数：sort函数，timsort 将插入排序与归并排序结合，其时间复杂度为O（nlog n）