计算机视觉 - 字典学习

在稀疏编码中，字典的学习至关重要。监督的字典学习方法大致可以分为3类。第一类为学习出针对所有信号的一个统一字典(universal dictionary)。该方法将字典学习与分类器训练完美的糅合为一个目标函数优化问题，旨在通过学习出的字典将信号的高维表示变得更加可分，可表示为

L(D,θ)=minD,θ∑i=1Nℓ(yi,f(xi,ψ(xi,D),θ))+λ∥θ∥22

其中 ℓ 为损失函数， f 为分类器， ψ 为信号的高维表示。此方法求解复杂度高，一般通过不断迭代得到一个近似解。尤其当类别数目比较多时，训练一个统一的字典和分类器将会非常耗时和低效。第二类方法为针对每一类别的信号学习出相应的子字典(category-specific dictionary)。 在学习过程中综合考虑信号的重构误差、稀疏度，以及结合不同类别信号的soft-max，fisher criteria，不同类别字典的不相关性，信号的类别约束等等，可表示为

L(D,A)=minD,A∑i=1C{∥Xi−DAi∥2F+λ∥Ai∥1}+S(A)

其中 D=[D1,⋯,DC] ， A=[A1,⋯,AC] ， S 为给类别辨别能量(discriminative power) 函数。 此方法能得到较好识别度的信号高维表示，但在测试过程中进行稀疏编码时只能考虑重构误差、稀疏度。其典型应用MCA，人脸识别。第三类即为前两类的结合。

1. SDL

文献 Supervised dictionary learning 发表于NIPS2009，属于第一类。文中的分类器 f 采用 f(x,α,θ)=θTα+b,θ∈Rk 或 f(x,α,θ)=xTθα+b,θ∈Rm×k ，信号的高维表示则采用稀疏表示模型，而最重要的损失函数采用的是logistics loss function， C(x)=log(1+ϱ−x) 。则最终的目标函数可变为

minD,θ,α∑i=1N{C(yif(xi,θ,αi))+λ0∥xi−Dαi∥22+λ1∥αi∥1}+λ2∥θ∥22

值得注意的是 yi∈{−1,1} ，前3项在式中称为损失函数 ℓ 。在测试时，通过学习到的字典进行稀疏编码，在通过下式预测样本类别。可统一的表示为

y=argminy∈{−1;1},θℓ(y,f(ψ(x,D),θ))

从上可知，比较该样本在不同类别下的损失函数值而预测样本。所以如果二者差值更大，那么就更加可分，继续优化得到：

L(D,θ)=minD,θ∑i=1N{C(ℓ(−yi,f(xi,ψ(xi,D),θ))−ℓ(yi,f(xi,ψ(xi,D),θ)))}+λ∥θ∥22

可以发现此式更难求解。可以将上式推广到多类别：a.直接法，则损失函数采用softmax discriminative cost function，如下式

Ci(x1,⋯,xp)=log(∑j=1pexj−xi)

针对每一类别学习一个模型 θi ，如何求解真是个问题；b.one-vs-all 或者 one-vs-one。其中图中的 S 函数即为文中定义的损失函数 ℓ 。大致分为两个步骤：

• 固定 D ，进行监督稀疏编码 α
• 固定 α ，采用投影梯度下降法(projected gradient descent)更新字典 D 和模型 θ

2. D-KSVD

该文Discriminative k-svd for dictionary learning in face recognition 发表在CVPR2010。方法算是对上述论文模型的简化，也属于第一类。损失函数没有采用logistic loss function，而是采用了更为简单类似于平方误差的损失函数，即 ℓ(yi,f(xi,ψ(xi,D),θ))=∥yi−f(xi,ψ(xi,D),θ)∥2 ，那么目标优化函数可以改写为

<D,W,A>=argminD,W,A∥X−DA∥2+λ∥A∥1+γ∥Y−WA∥2+β∥W∥2

其中 W 为线性分类器的参数矩阵(行数为类别数，列数为字典原子数目)， A 为训练数据的稀疏表示。 Y 为训练数据的标签矩阵，其每一列对应相应样本 x 的类别标签，即 yi=[0,0,⋯,1,⋯,0,0] ，非零位置即为所属类别。
该论文的有一贡献为作者使用了推广的K-SVD算法快速求解提出的模型。为了套用K-SVD算法，将模型变为下式

<D,W,A>=argminD,W,A∥∥∥∥(Xγ√Y)−(Dγ√W)A∥∥∥∥2+λ∥A∥1

注意，作者抛弃了正则项 β∥W∥2 。模型转化为了类似于标准的稀疏编码模型，则后续就可以采用经典的K-SVD算法进行字典更新。训练过程如下

• Train D with K-SVD
• Train W with equation: W=(ATA+βI)−1AYT

值得注意的是 (Dγ√W) 在训练时被一起归一化，那么最终得到的字典 D 与分类器参数矩阵 W 应该分别归一化。在测试样本时，直接使用分类器公式 f=Wα ，其中 f 中的最大元素对应的index即为预测的样本类别。

3. LC-KSVD

该文Learning a discriminative dictionary for sparse coding via label consistent k-svd 发表于CVPR2011，提出的方法实质是上文的一个改进，加入一个样本的label constant强约束，学习出一个辨别能力强的字典。模型可表示如下：

<D,W,A>=argminD,W,A∥X−DA∥2+λ∥A∥1+γ∥Y−WA∥2+β∥Q−A∥2

即加入了 β∥Q−A∥2 强约束，直观解释为强制使得到的稀疏表示 A 类似于 Q 。如何构造 Q 呢使得稀疏表示更加线性可分？文中提出 Q=[q1,⋯,qN]∈RK×N ，每一列代表对应样本希望学习出的稀疏表示。我们都知道稀疏表示向量中元素对应相应的字典列，那么如果样本 x 属于第 k 类，那么其对应的稀疏表示向量 q 中对应第 k 字典的元素设为1，而其它元素设为0，即 q=[0,⋯,0,1,⋯,1第k类,0,⋯,0]T 。由于其稀疏表示向量的形式，那么在初始化字典时，则应该分类别训练字典再合成为完整的一个初始化字典 D0 。
其中训练过程、算法，测试过程都与上文相似。注意上述提到的方法都是基于如下 {xi,yi}Ni=1 数据集，即每一个训练样本对应一个标签。当处理大分辨率图像数据集时，如CalTech时，一般做法是提取基于sift的spatial pyramid feature (3 levels)，再通过PCA降维，即得到该图像特征 x 。

4. FDDL

该文Fisher discrimination dictionary learning for sparse representation 于ICCV2011，提出的模型就是典型的第二种方法，辨别能量(discriminative power) 函数 S 为fisher discriminative criterion。简单的描述就是最小化类内分散(within-class scatter), SW(A) ；最大化类间分散(between-class scatter), SB(A) 。定义为

SW(A)SB(A)=∑Ci=1∑αk∈Ai(αk−mi)(αk−mi)T=∑i=1Cni(mi−m)(mi−m)T

其中 mi 与 m 分别是第 i 类训练数据和整个训练数据的高维表示的平均向量；在此作者提出 S(A)=tr(SW(A))−tr(SB(A))+η∥A∥2F 。
注意此类方法优化的目的是使得第 i 类数据完全由第 i 类子字典及对应的稀疏表示系数表示，最理想的情况是其它类的子字典对应的稀疏表示系数为0。 Xi 的表达式为 Xi≈∑CjDjAji=R1+⋯+Ri+⋯+RC 。所以本文作者在目标函数的重构误差上加入了如下项

∥∥Xi−DiAii∥∥2F+∑Cj=1j≠i∥∥DjAji∥∥2F

可直观的解释为如下图所示：

通过图(c)，加入的两项使得 Xi 与 Ri 更接近，而其它值 Rj 很小。那么最后的优化模型如下

L(D,A)=minD,A∑i=1C{∥Xi−DAi∥2F+∥∥Xi−DiAii∥∥2F+∑j=1j≠iC∥∥DjAji∥∥2F+λ∥Ai∥1}+S(A)

训练过程如下

• Updating A by fixing D . when D is fixed, the model is reduced to a sparse coding problem. The Iterative Projection Method (IPM) can be employed to the sparse coding problem class by class.
• Updating D (atom by atom, class by class) by fixing A .

测试：当训练样本相对较少时，测试样本则在整个字典下进行稀疏编码，得到的稀疏表示在各自类别的子字典下进行重构，以重构误差和稀疏表示到 mi 的距离的加权和作为最终的预测标准；当训练样本足够多时，测试样本则在每一个子字典下进行稀疏编码。

5. DL with structured incoherence

该方法Classi cation and clustering via dictionary learning with structured incoherence and shared features 于CVPR2010，属于第二类方法，辨别能量(discriminative power) 函数 S 为子字典之间的互相关性。加入子字典的相干性约束，使得相似的信号具有相似的稀疏表示。即信号在两个相关度较低的字典下，不能同时获得稀疏表示。模型如下

minD,A∑i=1C{∥∥Xi−DiAii∥∥2F+λ∥∥Aii∥∥1}+η∑i≠j∥∥DTiDj∥∥2F

注意此模型的重构误差项为在各自子字典下进行重构。测试时与传统方法一样，通过重构误差预测样本类别。

6. 基于监督的重构能量约束及非相干子字典学习

文献基于监督非相干字典学习的极化 SAR 图像舰船目标检测 于自动化学报2015，提出了一种结构化非相干字典学习算法，并成功的运用于极化SAR图像舰船目标检测。本文提出的模型是在第4与5节提出的模型上的一个融合，其将FDDL中的基于fisher discriminative creteria的辨别能量函数 S 改为子字典之间的互相关性，如第5小节所示。该改进模型具有如下特点：

• 良好的稀疏表示特性，即能获得小的重构误差
• 训练样本稀疏表示系数集中在其所属类别的子字典下，且在其它类别的子字典下重构能量小
• 子字典间具有较小的互相关性

这是一个典型的将目标检测问题转化为分类问题。本文采取的样本生成过程是在每一幅SR图像中在目标区域内运用阈值检测得到分辨单元作为目标训练样本，类别标记为2；在目标区域外的特定区域中选取分辨单元作为海杂波训练样本，类别标记为1。初始子字典的选取为在各自的样本集中随机选取一定数目样本组合成结构化初始字典。
由上可知，在学习阶段的稀疏重构是监督的，但是对于测试样本却并不知道该样本的类别。为了保持与训练阶段的一致性，作者在分类检测时做出了假设，即假设测试样本为第一类样本。另外，作者还定义了3个预测指标，a. D1 上的重构误差；b.对应 D2 上的稀疏表示系数的集中度；c.最终目标函数的值。做预测时，3个指标会有一个具体值，那么只需要设定一个阈值就可以判定假设是否成立。

7. 基于局部图拉普拉斯约束的低秩表示聚类}

该文基于局部图拉普拉斯约束的鲁棒低秩表示聚类方法 于自动化学报2015，针对传统的稀疏表示和低秩表示分类问题的缺陷，提出了基于局部图拉普拉斯约束的鲁棒低秩表示聚类模型。我们都知道，稀疏表示聚类方法针对每一个图像数据进行独立的稀疏编码，虽然获得了数据的稀疏性但忽略了图像子空间之间的结构属性；低秩表示聚类方法通过采用全局表示矩阵的秩作为约束，有效的利用了图像数据之间的相关性，虽然满足了表示矩阵的良好分块对角性质(即来自同一子空间的图像的非零表示系数构成一个小块)，但是其只关注了全局空间秩约束却忽略了图像数据据不相关性约束使得到的表示矩阵缺乏稀疏性。
抛开本文华丽的外衣，其提出的模型使得越接近的图像数据得出的低秩表示越接近。模型表示为

minD,Z,E∥Z∥∗+λ{∑i∑jωij∥∥Zi−Zj∥∥22}+μ∥E∥2,1s.t.X=D+E,D=DZ

其中 ωij 为图像数据 Xi 与 Xj 的权重，越接近其值越大。 Z 即为所求的分块对角矩阵表示。得到的分块对角矩阵就可以采用NCut进行聚类。

8. Inter-related Visual Dictionary Learning

本文Learning inter-related visual dictionary for object recognition 于CVPR2012，也是典型的第二类方法，提出的模型有效地解决类别之间相似而带来的识别挑战。该模型有效利用类别之间的相似性联合训练一个commonly shared dictionary 和 multiple category-specific dictionaries，为了增强字典的辨别性，同样引入了fisher判别准则。每一个类别子字典 Di 包含两部分：commonly shared dictionary D0 和对应的类别子字典 Di^ 。那么目标函数变为

min{D0,Di^,Ai}Ci=1∑i=1C{∥∥Xi−[D0,Di^]Ai∥∥2F+λ∥Ai∥1}+ηS(A)

注意这里的 Ai 为在对应子字典下的稀疏表示。 S(A) 为fisher判别准则，与FDDL类似。但不同的是式(5)中 SB 的求取。其中 mi 与 m 分别是第 i 类训练数据和整个训练数据在 D0 下的高维表示的平均向量。训练过程如下

• Updating A (class by class) by fixing D . In this work, two-step iterative shrinkage/thresholding(TwIST) algorithm is employed to update Ai .
• Updating D by fixing A . First update the category-specific dictionaries class by class and then update the shared dictionary D0 . Both the problem are least squares problems with quadratic constraints which can be efficiently solved using Lagrange dual.

在分类预测时，为了充分利用判别子字典下的辨别稀疏表示，本文提出的方法与之前的方法都不同。当得到各类别训练数据的稀疏表示时采用one-vs-all的策略训练出C个SVM分类器。预测新样本时，得到其在各个子字典下的稀疏表示，带入相应SVM中进行打分，最后分数最高的类别即为预测的样本类别。

9. Max-Margin Dictionary Learning (MMDL)

该文Max-margin dictionary learning for multiclass image categorization 于ECCV2010，首次提出将BoVW模型与分类器相结合，同时优化字典与分类器参数。该方法属于典型的第一类方法，与前述方法的区别在于信号的高维表示与损失函数，该文没有采用稀疏表示模型而是采用BoVW模型，且损失函数采用hinge-loss function。
这里假设图像训练数据集为 S={In,yn}Nn=1 ， yn={−1,1} ，而 In={xn1,⋯,xnNn} 是该图像的局部描述子集合，视觉单词定义为 D={d1,⋯,dK} 。那么在BoVW模型中，图像的特征表示为(soft-assignment)

ψ(In,D)=1Nn∑i=1Nnϕni,其中ϕni[k]=exp(−γ∥∥xni−dk∥∥22)∑k′Kexp(−γ∥∥xni−dk′∥∥22),k=1,⋯,K

传统的BoVW模型的视觉字典一般采用对所有训练数据集的局部描述子使用k-means非监督学习得到。而k-means方法以欧式距离最为度量，当两类数据非常相似时，则k-means方法则把这两类数据聚为一类。针对上述方法的缺陷，该文提出了最大化类间距的字典学习方法，即将分类器的学习糅合在一起。那么构造的优化目标函数为

minD,WL(D,W)=minD,W12∥W∥22+λ∑nNmax(0,1−ynWTψ(In,D))

优化上述目标函数旨在学习出字典使得最小化hinge-loss，同时学习出一个线性的SVM分类器。该模型的求解过程大致分为两步

• Updating W by fixing D . when D is fixed, the computation of W becomes a standard linear SVM problem.
• Updating D (atom by atom) by fixing W . Due to the presence of both the non-linearity of ψ(In,D) and the non-differentiability of the hinge loss, subgradient method is employed with the non-differentiable objective function. ℏn=max(0,1−ynWTψ(In,D)) , when ynWTψ(In,D)<1 , ℏn is differentiable:
  
  ∂ℏn∂dk=−2ynwkNn∑i=1Nnγ(xni−dk)(ϕni[k]−(ϕni[k])2);
  
  when when ynWTψ(In,D)>1 , ∇ℏn=0 . So,
  dk=dk−λ∑{n|ynWTψ(In,D)<1}∂ℏn∂dk
  
  These images that lie in the margin or are misclassified by W are named as effective images because only these images are involved in the dictionary update equation.

实验验证该方法比BoVW+SVM的分类准确率提高至少5%。

10. VLAD with Supervised Dictionary Learning

该文 Boosting vlad with supervised dictionary learning and high-order statistics 于ECCV2014，在标准的VLAD基础上引入了高阶(high-order)特征，并结合分类器一起构造目标函数学习出辨别的字典与分类模型。H-VLAD不但考虑了平均值信息，还引入了标准差，偏度等高阶信息。如下

vk=∑j=1Nk(xj−dk)=Nk(mk−dk)

其中 mk 为该图像数据 X 中被分配到第 k 类视觉单词 dk 的所有局部描述子的均值向量。由上式我们可以很轻易的发现尽管两类不同类别的数据的第 k 类局部描述子的分布完全不一样，但是其均值很有可能相近，则导致具有相似的特征表示，如下图：

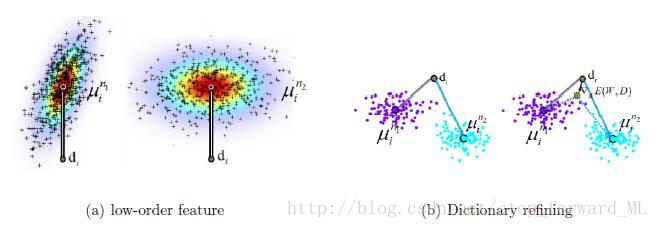
因此本文引入了高阶特征，标准差和偏度。

vck=σ2k^−σ2k=1Nk∑j=1Nk(xj−mk)2−σ2k

其中涉及的平方运算为向量中每个元素的平方， σ2k 为第 k 类局部描述子的协方差矩阵的对角元素。

vsk=γk^−γk=1Nk∑Nkj=1(xj−mk)3(1Nk∑Nkj=1(xj−mk)2)32−γk

其中涉及的平方运算为向量中每个元素的平方， γk 为第 k 类局部描述子的偏度。
无论是BoVW还是VLAD对字典都非常敏感，学习一个辨别的字典增强信号的区分能力。损失函数采用logistic loss function，则目标函数变为

E=minD,W∑n=1Nlog[1+exp(−ynWTϕn)]+λ∥W∥22

其中 yn={−1;1} , ϕn=[ϕn[1],⋯,ϕn[K]] , ϕn[k]=[vk,vck,vsk]T 。在求解该模型时，采用梯度下降， ∇WE 和 ∇dkE 可求。