计算三角形平面的的法线
Vector的叉乘,可算出法线
设有按逆时针方向设置的一个三角形,
var triangle = [
-0.5, -0.5, 0.0, // v0
0.5, -0.5, 0.0, // v1
0.0, 0.5, 0.0 // v2
];

先将这三个顶点转换为Vector:
var v0 = new J3DIVector3(triangle[0], triangle[1], triangle[2]); var v1 = new J3DIVector3(triangle[3], triangle[4], triangle[5]); var v2 = new J3DIVector3(triangle[6], triangle[7], triangle[8]);
之后,两两进行叉乘,以得到其法线。
// counter-clock-wise cross product var normal = v0 * v1; // (0.0, 0.0, 0.5) var normal = v1 * v2; // (0.0, 0.0, 0.25) var normal = v2 * v0; // (0.0, 0.0, 0.25) // clock-wise cross product var normal = v1 * v0; // (0.0, 0.0, -0.5) var normal = v2 * v1; // (0.0, 0.0, -0.25) var normal = v0 * v2; // (0.0, 0.0, -0.25)
由于三角形的正面朝向用户,因此,正确的法线方向也应朝向用户。而上面的六种结果中,只有前面三个结果是正确的。
可见,在按逆时针设置的三角形中,只要按逆时针取出任意两点进行叉乘,就可得出正确的平面法线方向。
用这种方式求三角形平面的法线正确吗?也对,也不对。我们无意中犯了一个错误。在上面定义三角形顶点的代码中,由于三个顶点的Z轴坐标均为0,导致这个三角形平面垂直于Z轴,从而犯了一个概念混淆的错误:直接将顶点转换为Vector了。三角形的顶点不是Vector!
取消特殊化
先将V2脱离Z轴。

再将各顶点与坐标系原点连接。
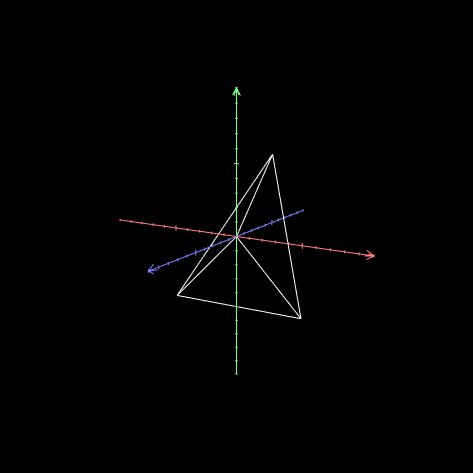
此图可清晰地看出,顶点是原点到各顶点的距离,也即顶点在坐标系中的位置。而我们要求出与三角形平面垂直的法线,应将两条相交的边进行叉乘,才能得到正确的结果。也即,三条边才是求得法线的矢量。
修改代码:
var point3 = function(x, y, z) {
return {x:x, y:y, z:z};
};
var pt0 = point3(-0.5, -0.5, -0.0);
var pt1 = point3( 0.5, -0.5, -0.0);
var pt2 = point3( 0.0, 0.5, -0.5);
var triangle = [
pt0.x, pt0.y, pt0.z,
pt1.x, pt1.y, pt1.z,
pt2.x, pt2.y, pt2.z
];
我们取相交于pt0的两条边作为矢量。即pt0到pt1, pt0到pt2的的两条边。
根据矢量运算规律,原点到pt0的矢量减去原点到pt1的矢量,可以得到pt0到pt1的矢量。同理,原点到pt0的矢量减去原点到pt2的矢量,可以得到pt0到pt2的矢量。
var v0 = new J3DIVector3(pt0.x, pt0.y, pt0.z);
var v1 = new J3DIVector3(pt1.x, pt1.y, pt1.z);
var v2 = new J3DIVector3(pt2.x, pt2.y, pt2.z);
var v01 = sub(v0, v1);
var v02 = sub(v0, v2);
function sub(vector1, vector2) {
return new J3DIVector3(vector1[0] - vector2[0], vector1[1] - vector2[1], vector1[2] - vector2[2]);
}
之后,根据这两个矢量求得法线,并归一化。
var normal = getNoramlFromVector(v01, v02);
normal.divide(normal.vectorLength());
function getNoramlFromVector(v1, v2) {
var normal = new J3DIVector3(v1[0], v1[1], v1[2]);
normal.cross(v2);
return normal;
}

将原点到三角形各顶点的连线去掉,可清楚地看到这条法线垂直于三角形平面的效果。
