MATLAB系列笔记:二维绘图(二)
0x00 前言
文章中的文字可能存在语法错误以及标点错误,请谅解;
如果在文章中发现代码错误或其它问题请告知,感谢!
MATLAB版本:MATLAB R2018b。
0x01 不同坐标系下的绘图命令
1.极坐标系下绘图
在MATLAB中需要用到polar命令来绘制极坐标系下的函数图像。polar命令调用格式如下:
| 调用格式 | 说明 |
|---|---|
| polar(theta,rho) | 在极坐标中绘图,theta的元素代表弧度,然后代表极坐标矢径 |
| polar(theta,rho,s) | 在极坐标中绘图,参数s的内容与plot命令相似 |
例1:
在直角坐标系与极坐标下画出下面的函数图像:
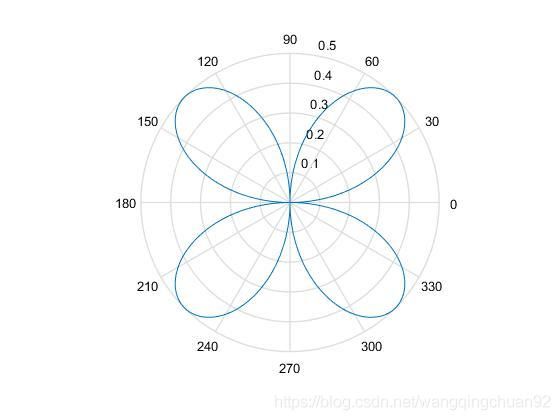
r = |sintcost|
>> t = 0:0.01:4*pi;
>> r = abs(sin(t).*cos(t));
>> polar(t,r)
例2:
在直角坐标和极坐标中画出以下函数的图像:
r = e s i n t − 2 s i n 4 t + ( c o s t 5 ) 6 r = e^{sint} - 2sin4t + (cos\frac{t}{5})^6 r=esint−2sin4t+(cos5t)6
>> t = linspace(0,24*pi,10000);
>> r = exp(sin(t))-2*sin(4.*t)+(cos(t./5)).^6;
>> subplot(2,1,1),plot(t,r)
>> subplot(2,1,2),polar(t,r)
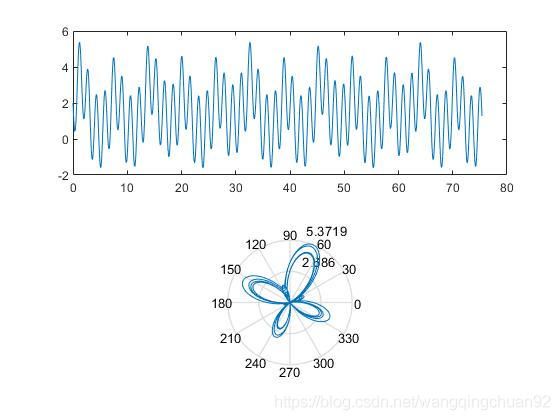
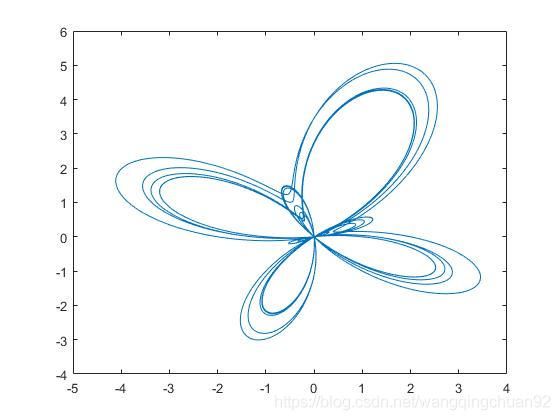
若想要看一下此图在直角坐标系下的图像,则可以借助pol2cart命令,可以将相应的极坐标数据点转化为直角坐标系下的数据点:
>> [x,y] = pol2cart(t,r);
>> figure
>> plot(x,y)
2.半对数坐标系下绘图
半对数坐标在工程中也是很常见MATLAB提供semilogx与semilogy命令可以实现。semilogx命令用来绘制x轴为半对数的曲线,semilogy命令用来绘制y轴为半对数坐标的曲线,他们的使用格式是一样的。
| 调用格式 | 说明 |
|---|---|
| semilogx(X) | 绘制以10为底对数刻度的x轴和线性刻度的y轴的对半数坐标曲线,若X是实矩阵,则按列绘制每列元素值相对其下标的曲线图,若为复矩阵,则等价于semilogx(real(X),imag(X))命令 |
| semilogx(X1,Y1,…) | 对极坐标(Xi,Yi)(i = 1,2,…)绘制所有曲线,如果(Xi,Yi)是矩阵,则以(Xi,Yi)对应的行或列元素为横纵坐标绘制曲线 |
| semilogx(X1,Y1,s1,…) | 对极坐标(Xi,Yi)(i = 1,2,…)绘制所有曲线,其中si是控制曲线类型、标记以及彩色的参数 |
| semilogx(…,‘PropertyName’,PropertyValue,…) | 对所有semilogx命令生成的图形对象的属性进行设置 |
| h = semilogx(…) | 返回line图形句柄向量,每条线对应一个句柄 |
例3:
比较函数y=10x 在半对数坐标系与直角坐标系下的图像。
>> x = 0:0.01:1;
>> y = 10.^x;
>> subplot(1,2,1),semilogy(x,y)
>> subplot(1,2,2),plot(x,y)
3.双对数坐标系下绘图
除了半对数坐标绘图外,MATLAB还提供双对数坐标系下的绘图命令 loglog,使用方法和semilogx一样。
例4:
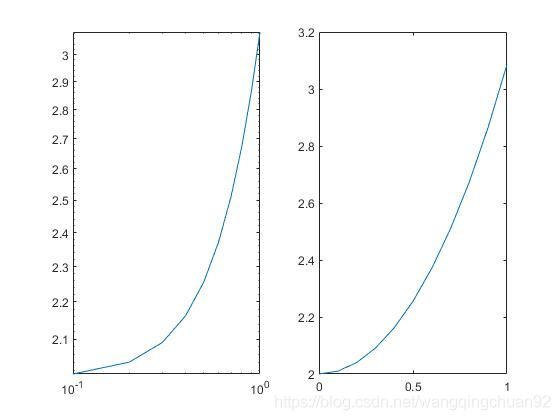
比较函数y = ex + e-x 在双对数坐标系与直角坐标系下的图像。
>> x = 0:0.1:1;
>> y = exp(x)+exp(-x);
>> subplot(1,2,1),loglog(x,y)
>> subplot(1,2,2),plot(x,y)
4.双y轴对标
双y坐标在实际中常用来比较两个函数图像,MATLAB中提供plotyy实现,使用格式如下:
| 调用格式 | 说明 |
|---|---|
| plotyy(x1,y1,x2,y2) | 用左边的y轴画出x1对应于y1的图,用右边的y轴画出x2对应的y2的图 |
| plotyy(x1,y1,x2,y2,‘function’) | 使用字符串’function’指定的绘图函数产生每一个图形,‘function’可以是plot、semilogx、semilogy、stem或任何满足h=function(x,y)的MATLAB函数 |
| plotyy(x1,y1,x2,y2,‘function1’,‘function2’) | 使用function1(x1,y1)为左轴画出图形,使用function2(x2,y2)为右轴画出图形 |
例5:
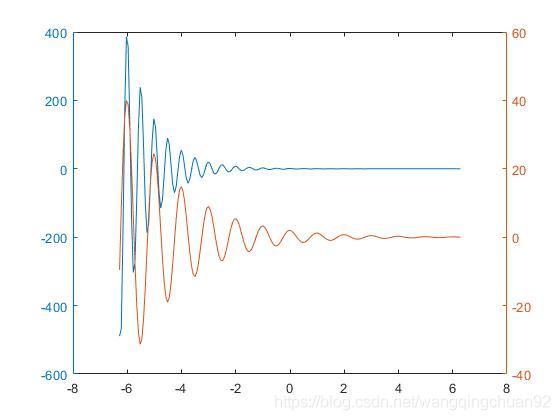
用不同标度在同一坐标内绘制曲线y1 = e-x cos4 π \pi πx和y2 = 2e-0.5x cos2 π \pi πx。
>> x = linspace(-2*pi,2*pi,200);
>> y1 = exp(-x).*cos(4*pi*x);
>> y2 = 2*exp(-0.5*x).*cos(2*pi*x);
>> plotyy(x,y1,x,y2,'plot')
以上。
参考文档:
1.https://www.zybuluo.com/codeep/note/163962(Markdown 公式指导手册)
2.https://blog.csdn.net/katherine_hsr/article/details/79179622(数学符号和公式)
3.天工在线.中文版MATLAB2018从入门到精通(实战案例版)[M].北京:中国水利水电出版社,2018.