自定义一组基函数的最佳平方逼近——matlab实现
作者:老李
时间:2019-10-26
目标:
给出一组非线性相关的函数作为基底,通过有限点集 ( x k , y k ) (x_{k},y_{k}) (xk,yk),构造拟合函数
过程:
我们设这个基底为 { f i ( x ) } , i = 1 , 2 , . . . M \left \{f _{i}(x)\right \},i= 1,2,...M {fi(x)},i=1,2,...M
我们的目标是,对于每一个 x k x_{k} xk寻找一系列 c i c_{i} ci,使得 E = ∑ k = 1 n ( c i f i ( x k ) − y k ) 2 E = \sum_{k=1}^{n}(c_{i}f _{i}(x_{k})-y_{k})^{2} E=∑k=1n(cifi(xk)−yk)2最小。
我们使用最一般的方法:将E对每一个参数 c i c_{i} ci进行求导,然后令其导函数为零,最后求出其值。
∂ E ∂ c i = ∑ k = 1 N ( ( ∑ j = 1 M c j f j ( x k ) ) − y k ) f i ( x k ) = 0 , i = 1 , 2 , . . . M (1) \frac{\partial E}{\partial c_{i}} = \sum_{k = 1}^{N}((\sum_{j=1}^{M}c_{j}f_{j}(x_{k}))-y_{k}) f_{i}(x_{k})= 0,i = 1,2,...M \tag{1} ∂ci∂E=k=1∑N((j=1∑Mcjfj(xk))−yk)fi(xk)=0,i=1,2,...M(1)
为了实现矩阵化操作,我们想要将所求的系数 c i c_{i} ci分离出来,于是我们改变求和的次序,可得: ∑ j = 1 M ( ∑ k = 1 N f i ( x k ) f j ( x k ) ) c j = ∑ k = 1 N f i ( x k ) y k (2) \sum_{j = 1}^{M}(\sum_{k = 1}^{N}f_{i}(x_{k})f_{j}(x_{k}))c_{j}=\sum_{k=1}^{N}f_{i}(x_{k})y_{k}\tag{2} j=1∑M(k=1∑Nfi(xk)fj(xk))cj=k=1∑Nfi(xk)yk(2)
最后我们对其实现矩阵化操作:
我们令 F = [ f 1 ( x 1 ) f 2 ( x 1 ) ⋯ f M ( x 1 ) f 1 ( x 2 ) f 2 ( x 2 ) ⋯ f M ( x 2 ) ⋮ ⋮ ⋱ ⋮ f 1 ( x N ) f 2 ( x N ) ⋯ f M ( x N ) ] F= \left[ \begin{matrix} f_{1}(x_{1}) & f_{2}(x_{1}) &\cdots & f_{M}(x_{1}) \\ f_{1}(x_{2}) & f_{2}(x_{2}) &\cdots& f_{M}(x_{2}) \\ \vdots&\vdots&\ddots&\vdots\\ f_{1}(x_{N}) & f_{2}(x_{N}) & \cdots& f_{M}(x_{N})\\ \end{matrix} \right] F=⎣⎢⎢⎢⎡f1(x1)f1(x2)⋮f1(xN)f2(x1)f2(x2)⋮f2(xN)⋯⋯⋱⋯fM(x1)fM(x2)⋮fM(xN)⎦⎥⎥⎥⎤可以将(2)式用矩阵表达出来 F ′ F C = F ′ Y F'FC =F'Y F′FC=F′Y
求得的系数矩阵 C C C为 C = ( F ′ F ) − 1 F ′ Y C = (F'F)^{-1}F'Y C=(F′F)−1F′Y
我用matlab实现了这个过程,代码如下:
吐槽一点,csdn粘贴matlab代码挺麻烦的
function [ C ,err] = leastSquareApprox( X,Y,fun)
%leastSquareApprox: least square approximation by linear combination of nonlinear correlation equations
% Input: X is the 1*n abscissa vector
% : Y is the 1*n ordinate vector
% : fun is the n*1 based function
% Output: C is the coefficient list for the function
% : err is the maximum of the least square approximation for each point
if (length(X) ~= length(Y))
error('wrong size');
else
n = length(X);
X0 = reshape(X,n,1);
F = subs(fun, X0);
C = (pinv(F'*F))*F'*Y;
Xt = min(X):0.1:max(X);
ft = subs(fun, Xt')*C;
scatter(X,Y);
hold on;
plot(Xt,ft,'r');
hold off;
f0 = subs(fun, X)*C;
err = max((f0-Y).^2);
end
end这里需要特别注意的一点是输入的fun这个参数,是我们作为最小二乘拟合(最佳平方逼近)的函数。
这里我来展示一下怎么去实现这个基函数。
这里,我的基函数通过符号变量来表达,
我们可以选择多项式作为基底,当我们输入记得的数量n时,该基底可以表示为
{ 1 , x , x 2 , x 3 , ⋯ , x n − 1 } \left \{1,x,x^2,x^3,\cdots,x^{n-1}\right \} {1,x,x2,x3,⋯,xn−1}
(如果我们不去讨论这组基的具体在所张成的空间的定义,或者说不一定要符合在该空间多定义出的的正交这一性质的话,也就是说我们只要保证基底中的元素不能直接相互表示的话)
我们可以写一段程序来实现它:(syms和sym 用来定义符号变量)
n = input('please input the size of the data ');
syms x;
B = sym(zeros(1,n));
for i = 0:n-1
B(i+1) = x.^i;
end这样,我们就把作为基底的多项式输出出来了。
效果
假设我们只输入五个点:对应的自变量X=[1,2,3,4,5]和因变量Y=[15,64,84,12,34]
这里我先选用3个基底(n=3)来进行拟合,也就是二次函数拟合:
得到的效果如下:
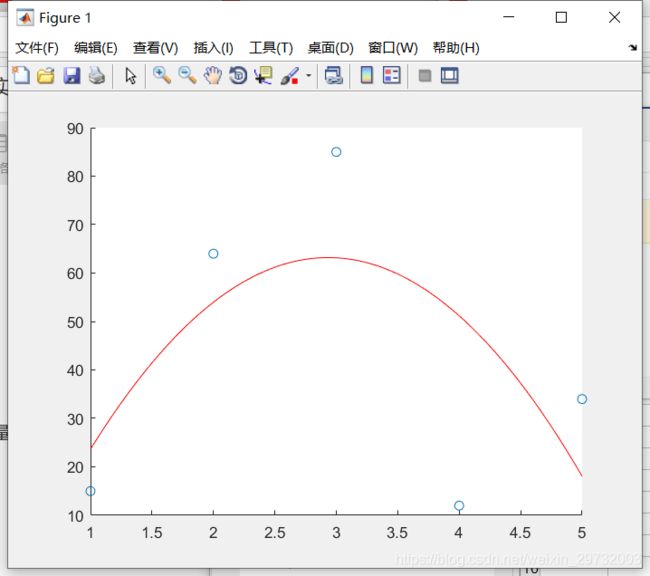
输出的数值为:
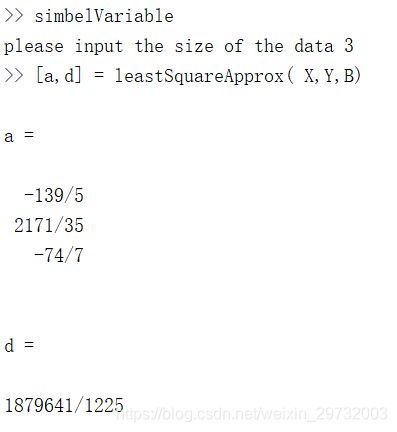
其中误差为d
关于误差的讨论
已知i我们输入的为5个点,n为基底中元素的个数
当我们令n=5时,由范德蒙德行列式,我们可以知道,当我们输入的点不同时,该行列式的值不为0,也就是说,插值函数是具有唯一性的。也就是说,无论我们用的是拉格朗日插值还是牛顿插值,还是这里用到的矩阵运算,我们得到的东西是一样的。而不同的插值方法的功效主要还是体现在计算机的运行效率上,比如牛顿插值用到了递归的方法从而节约了运算的时间。
当我们把n变为>5的数,我们可以保证逼近出来的曲线是过每一个点的,所得出来的误差应该为0。但由于插值函数的唯一性,我们不应该认为这是插值,但这样的一个方法应该叫什么,我现在并不清楚,也许以后会学到并理解。
写在最后
1.在计算机实现逼近的过程中,输入的变量与输出的变量一定是离散且有限的,也就是说,在计算机数值计算中,我们用的大多为 ∑ \sum ∑而不是 ∫ \int ∫。
2.假如我们输入的是N个点,假如我们使用的基底(不能相互表示)中元素的数量是>=N的,那我们逼近出来的曲线一定是过我们输入的每一个点的,(=N的时候是为插值)。
3.同样,我们也可以注意到,其实DFT算法的核心思想与我今天所写的其实是一致的。唯一不同的是他运用的是 e − 2 π i m N e^{-\frac{2\pi im}{N}} e−N2πim作为基底,其中 m = 0 , 1 , 2 , ⋯ , N − 1 m = 0,1,2,\cdots,N-1 m=0,1,2,⋯,N−1。

