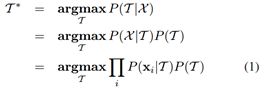Abstract
针对用于多目标跟踪的数据关联(data association),本文提出了一种基于网络流(network flow)的优化方法。将最大后验概率(maximum-a-posteriori:MAP)数据关联问题映射到满足轨迹上非重叠(non-overlap)约束的成本流网络(cost-flow network)。通过网络的最小成本流算法(a min-cost flow algorithm),可找到最优的数据关联。扩展该网络:包含一个显式遮挡模型(EOM),可用于处理存在长时间(long-term)目标间遮挡(inter-object occlusions)现象的跟踪。在原算法基础上,采用迭代法可求解基于EOM的网络。轨迹的初始化和终止以及潜在的假观测(potential false observations)都由该框架内在地建模。该方法效率高,并且不需要假设剪枝(hypotheses pruning)。在两个公开的行人数据集上,通过与之前的研究结果进行性能比较,说明了本方法的改进效果。
1. Introduction
目标检测和跟踪的鲁棒性对于许多计算机视觉任务都非常重要。我们讨论的方法是:将每帧图像的目标检测结果作为输入,然后将检测结果关联起来以寻找目标轨迹。并不是所有目标都能在每一帧中被检测到,并且可能存在错误检测,还有一些目标可能被其他目标遮挡;这些因素使得数据关联成为一项困难的任务。
一些方法,如[1,2],试图解决每一帧中的歧义。其他的,例如[3,4,5,6,7,8,9,10]则使用更多的全局信息。然而,这些备选方案的搜索空间随着帧数的增加呈指数级增长,这就需要严格限制搜索窗口以及进行假设剪枝。它们通常还假设所有的检测结果都是正确的,但实际上并不能保证总是正确。
我们提出了一种有效的全局数据关联方法,相比以前的方法,它可以为长的多的序列(窗口)找到最优解。在我们的方法中,数据关联被定义为给定一组目标检测结果作为输入观测值的MAP估计问题。将非重叠轨迹假设建模为成本流网络中的不相交流路径(disjoint flow path);观测似然和转换概率(observation likelihood and transition probabilities)被建模为流成本。采用最小成本流算法可得到全局最优轨迹关联。为处理长时间遮挡情形下的跟踪,通过向网络中添加遮挡节点和约束(只考虑目标之间的遮挡inter-object occlusions),建立显式遮挡模型(EOM)。在原最小成本流算法的基础上,采用迭代法求解基于EOM的网络的最小成本流(a minimal cost flow)。轨迹初始化、终止和目标遮挡推断是该方法的内在行为,因此可以从关联结果中推断出来这些信息。从跟踪结果推断遮挡和漏检的一个例子如图1所示。
本文的其余部分组织如下。相关工作将在第2节中讨论。第3节描述了MAP formulation和及其全局最优解。第4节介绍了显式遮挡模型(EOM)及其迭代求解方法。第5节中给出实现细节。实验结果见第6节。结论见第7节。
2. Related work
要跟踪多个目标,一种方法是逐帧(或在一个小的时间窗口内)做出数据关联决策,如[1,2]。虽然这种方法已经显示出不错的性能,但是在做出关联决策之前考虑更多的帧通常来说应该有助于更好地克服长时间遮挡和误检或漏检造成的歧义。
许多使用更多信息的全局方法已被尝试用来克服检测错误的影响。一种策略是通过整个序列一次优化一个轨迹;这在基于动态规划的方法中已被采用,如[5,6]。然后使用贪婪策略来组合这些轨迹并处理潜在的冲突。由于轨迹是单个分别优化的,这些方法很难对遮挡进行建模。另一种方法是同时优化多个轨迹;多假设跟踪(MHT:multi-Hypothesis Tracking)[3]和联合概率数据关联滤波器(JPDAF:Joint Probabilistic Data Association Filters)[4]是两个具有代表性的例子。此外,在[10]中,检测和轨迹假设的估计与二次布尔规划结合在一起。由于假设搜索空间是组合的(combinatorial),这类方法只能在有限的时间窗口内进行优化,还必须对假设进行剪枝。采样方法例如MCMC[9]同样被用来求解类似问题。在这些方法中,遮挡通常被建模为轨迹的合并和拆分(merging and splitting of trajectories)。
Tracklet Stitching[8]和基于线性规划(LP)的跟踪[7]是寻求在整个序列上同时优化所有轨迹的另外两种方法。[8]首先生成tracklets,它是由检测响应(detection responses)经保守分组形成的轨迹片段(fragments of tracks)。然后使用匈牙利划分算法连接tracklets。这种方法假设所有tracklets都对应于真实的目标轨迹,因此很难适用到原始检测结果,即每一帧中可能出现许多假警(false alarms)。[7]为每个对象轨迹构建一个子图集合,这些子图之间的边(edges)表示对象交互(object interactions)。然后通过线性规划和舍入近似地求解子图集上的多路径搜索问题。它需要假设目标间位置(inter-object positions)相对稳定、目标个数固定。
3. Our approach
我们定义数据关联为MAP问题。然后将MAP问题映射到成本流网络(a cost-flow network),并用最小成本流算法(a min-cost flow algorithm)求解。这样映射是基于寻找非重叠目标轨迹与在图中寻找边不相交路径(edge-disjoint paths)之间存在相似性;后者可以通过网络流算法得到有效的求解。我们首先提出构想,然后提供最小成本流求解方法。
3.1 非重叠约束下的MAP
3.2 最小成本流求解方法
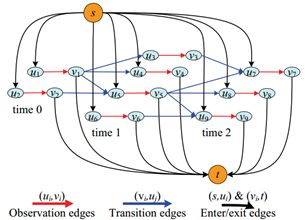
图2 成本流网络的一个例子,包含3个时间步长和9个观测
• Construct the graph G(V, E, C, f) from observation set X
• Start with empty flow
• WHILE ( f(G) can be augmented )
– Augment f(G) by one.
– Find the min cost flow by the algorithm of [12].
– IF ( current min cost < global optimal cost )
Store current min-cost assignment as global optimum.
• Return the global optimal flow as the best association hypothesis
Algorithm 1:Find MAP trajectories by min-cost flow
算法1为数据关联提供了一个通用框架。该方法不同于单独优化各轨迹的方法,也不受困于假设空间组合激增的方法,它能够有效率地找到全局最优解。接下来,我们扩展我们的方法来处理长时间遮挡的跟踪。
4.Explicit Occlusion Model(EOM)
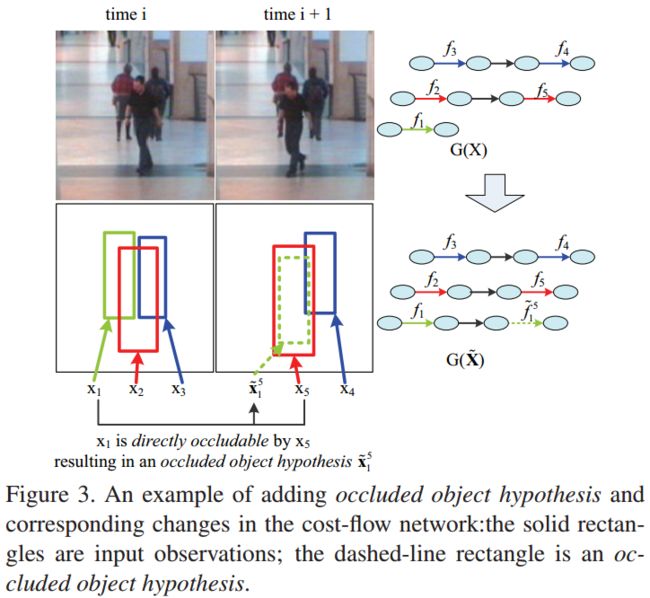
添加occlusion hypotheses
添加occlusion constraint
求解
通常,算法在迭代两轮之后就可以得到最优解。