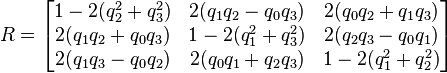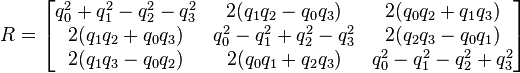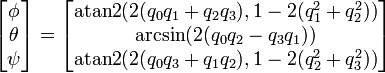三维坐标下的旋转

　  三维坐标的旋转有以下几种常见的表示形式：旋转向量，旋转矩阵，欧拉角，四元数,下面对这四种表示形式及其之间的转换进行介绍

旋转向量

　　通常为3x1的列向量，向量方向即为旋转轴，向量的模表示绕轴逆时针旋转的角度,如旋转向量v=[a,b,c],那么旋转角度theta=sqrt(a²+b²+c²),旋转轴z=[a/theta, b/theta, c/theta]

旋转矩阵

　　旋转矩阵用3x3的矩阵表示，旋转矩阵是正交矩阵，且行列式是单位1   　　　　　　　　　

　　　　　　   

　　　　　　 det(R)=1                                                     　　

　　旋转向量与旋转矩阵可以通过罗德里格斯(Rodrigues)变换进行转换。opencv实现Rodrigues变换的函数是：

　　　　　　　　int cvRodrigues2( const CvMat* src, CvMat* dst, CvMat* jacobian=0 );

　生成旋转矩阵的一种简单方式是把它作为三个基本旋转的序列复合，如下面要介绍的欧拉角的复合。 

欧拉角

　　欧拉角度的基本思想是将旋转分解为绕三个互相垂直轴的三个旋转组成的序列。使用欧拉角，就要指明坐标系系统以及旋转顺序。最常用的约定，即所谓“roll-pitch-yaw”系统。偏航角——Yaw，俯仰角——Pitch,翻滚角——Rool

　　下面讨论欧拉角与旋转矩阵之间的转换，绕x，y，或z轴旋转θ的矩阵为：

 　　　　

　　要计算最终的旋转，只需按一定的顺序将R_x(θ),R_y(θ),R_z(θ)做矩阵乘法，所以顺序不同，最终的旋转矩阵结果也不同。如果规定了坐标系以及旋转顺序，那么旋转矩阵是惟一的。

　　欧拉角表示的旋转会造成万向节锁（Gimbal Lock）的现象。所谓万向节锁简单的说是指（经过绕某个轴的旋转后）物体的两个旋转轴指向同一个方向，从而失去一维自由度，接下来无论如何也旋转不出某种状态。由于万向节锁的存在，欧拉旋转无法实现球面平滑插值。

四元数

　　一个四元数可以表示为q = w + xi + yj + zk，i、j、k是一种特殊的虚数单位（类比虚数表示中的i,j），并有以下运算规则：i⁰=j⁰=k⁰=1，i²=j²=k²=-1， |q|²=w²+x²+y²+z²=1,四元数的其他性质不在一一叙述。

       四元数指明了旋转的角度和旋转轴，如旋转轴的方向余弦为（cosβ_x,cosβ_y,cosβ_z）,旋转角为α，则对应的四元数q=[q₀,q₁,q₂,q₃]，其中 

                      

　　 四元数与旋转矩阵之间的转换关系（注意利用模为1的性质有一下两种表示方法）

                            或                  ，

　　  旋转矩阵转换为四元数：

　　　　　　

　　　　m_ij表示旋转矩阵中第i行k列的元素

           四元数转换为欧拉角：

　　　 首先定义

　　　  Roll – : rotation about the X-axis

            Pitch – : rotation about the Y-axis

            Yaw – : rotation about the Z-axis

            则对应的转换为

           

            如果已知欧拉角求四元数，可以先将欧拉角转化为旋转矩阵，再由旋转矩阵求四元数

 

原创文章，转载请注明出处

 

 

 

转载于:https://www.cnblogs.com/xtl9/p/5445353.html