SHA 加密算法
SHA 加密算法
-
算法简介
SHA安全散列算法SHA (Secure Hash Algorithm,SHA)
是美国国家标准技术研究所发布的国家标准FIPS PUB 180,最新的标准已经于2008年更新到FIPS PUB 180-3。其中规定了SHA-1,SHA-224,SHA-256,SHA-384,和SHA-512这几种单向散列算法。SHA-1,SHA-224和SHA-256适用于长度不超过2^64二进制位的消息。SHA-384和SHA-512适用于长度不超过2^128二进制位的消息。
散列是信息的提炼,通常其长度要比信息小得多,且为一个固定长度。加密性强的散列一定是不可逆的,这就意味着通过散列结果,无法推出任何部分的原始信息。任何输入信息的变化,哪怕仅一位,都将导致散列结果的明显变化,这称之为雪崩效应。散列还应该是防冲突的,即找不出具有相同散列结果的两条信息。具有这些特性的散列结果就可以用于验证信息是否被修改。
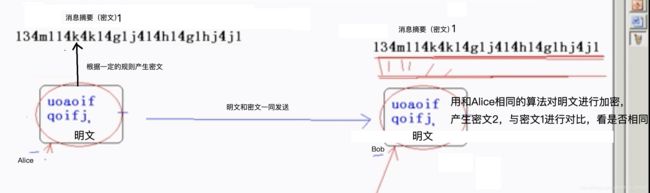
图1: SHA加密算法流程简图
-
SHA加密算法用途
数字签名、数字时间戳、数字证书
比如:数字签名,在传送过程中,Alice不可能真正签一个名字“Alice”,同消息一块儿传送给Bob。(这样容易被发现,或被攻击?被篡改?)而是通过一定的加密规则,将明文和密文一块儿传送给Bob,让Bob再根据加密规则,判断密文准确与否。
-
SHA加密原理以及流程
在SHA1算法中,我们必须把原始消息(字符串,文件等)转换成位字符串位。SHA1算法只接受位作为输入。假设我们对字符串“abc”产生消息摘要。首先,我们将它转换成位字符串如下:
01100001 01100010 01100011
―――――――――――――
‘a’=97 ‘b’=98 ‘c’=99这个位字符串的长度为24。
下面我们需要5个步骤来计算SHA。
3.1 补位
消息必须进行补位,以使其长度在对512取模以后的余数是448。也就是说,(补位后的消息长度)len%512 = 448。即使长度已经满足对512取模后余数是448,补位也必须要进行(eg: 消息长度 len1=448,len1%512 = 448,但仍要再补512位,使len1’=448+512=960)。
补位是这样进行的:先补一个1,然后再补0,直到长度满足对512取模后余数是448。总而言之,补位是至少补一位,最多补512位(言下之意:不可能1位都不补)。还是以前面的“abc”为例显示补位的过程。
原始信息: 01100001 01100010 01100011
补位第一步:01100001 01100010 01100011 1
首先补一个“1”
补位第二步:01100001 01100010 01100011 10…..0
然后补423个“0”
我们可以把最后补位完成后的数据用16进制写成下面的样子
61626380 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000
现在,数据的长度是448了,我们可以进行下一步操作。
3.2 补长度
所谓的补长度是将原始数据的长度补到已经进行了补位操作的消息后面。通常用一个64位的数据来表示原始消息的长度。在进行了补长度的操作以后,整个消息就变成下面这样了(16进制格式)
61626380 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000018
如果原始的消息长度超过了512,我们需要将它补成512的倍数。然后我们把整个消息分成一个一个512位的数据块,分别处理每一个数据块(即SHA一次性最多加密64个字节,512个比特位),从而得到消息摘要(即我们所谓的密文)。
3.3 使用的常量
一系列的常量字K(0), K(1), ... , K(79),如果以16进制给出。它们如下:
Kt = 0x5A827999 (0 <= t <= 19)
Kt = 0x6ED9EBA1 (20 <= t <= 39)
Kt = 0x8F1BBCDC (40 <= t <= 59)
Kt = 0xCA62C1D6 (60 <= t <= 79)
3.4 需要使用的函数
在SHA1中我们需要一系列的函数。每个函数ft (0 <= t <= 79)都操作32位字B,C,D并且产生32位字作为输出。ft(B,C,D)可以如下定义
ft(B,C,D) = (B AND C) OR ((NOT B) AND D) ( 0 <= t <= 19)
ft(B,C,D) = B XOR C XOR D (20 <= t <= 39)
ft(B,C,D) = (B AND C) OR (B AND D) OR (C AND D) (40 <= t <= 59)
ft(B,C,D) = B XOR C XOR D (60 <= t <= 79).
3.5 计算消息摘要
必须使用进行了补位和补长度后的消息来计算消息摘要。计算需要两个缓冲区,每个都由5个32位的字组成,还需要一个80个32位字的缓冲区。第一个5个字的缓冲区被标识为A,B,C,D,E。第一个5个字的缓冲区被标识为H0,H1, H2, H3, H4
。80个字的缓冲区被标识为W0, W1,..., W79
另外还需要一个一个字的TEMP缓冲区。
为了产生消息摘要,在第4部分中定义的16个字的数据块M1, M2,..., Mn
会依次进行处理,处理每个数据块Mi 包含80个步骤。
在处理每个数据块之前,缓冲区{Hi} 被初始化为下面的值(16进制)
H0 = 0x67452301 由于SHA算法采用大端存储模式:所以H0中实际的数字是 0x01234567
H1 = 0xEFCDAB89 同理,H1中实际存储的数字是 0x89ABCDEF
H2 = 0x98BADCFE 同理,H2中实际存储的数字是 0xFEDCBA98
H3 = 0x10325476 同理,H3中实际存储的数字是 0x76543210
H4 = 0xC3D2E1F0. 同理,H4中实际存储的数字是 0xF0E1D2C3
现在开始处理M1, M2, ... , Mn。为了处理 Mi,需要进行下面的5个步骤
(1). 将 Mi 分成 16 个字 W0, W1, ... , W15, W0 是最左边的字
(2). 对于 t = 16 到 79 令 Wt = S1(Wt-3 XOR Wt-8 XOR Wt- 14 XOR Wt-16).
(3). 令 A = H0, B = H1, C = H2, D = H3, E = H4.
(4) 对于 t = 0 到 79,执行下面的循环
TEMP = S5(A) + ft(B,C,D) + E + Wt + Kt;
E = D; D = C; C = S30(B); B = A; A = TEMP;
(5). 令 H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.
在处理完所有的 Mn, 后,消息摘要是一个160位的字符串
即得到密文:H0 H1 H2 H3 H4.
-
注意事项
SHA加密算法采用的是 大端存储模式,即高位数据放在低地址,低位数据放在高地址