Leetcode中组合总和系列
一、Leetcode77. 组合
1、题目
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
2、思路
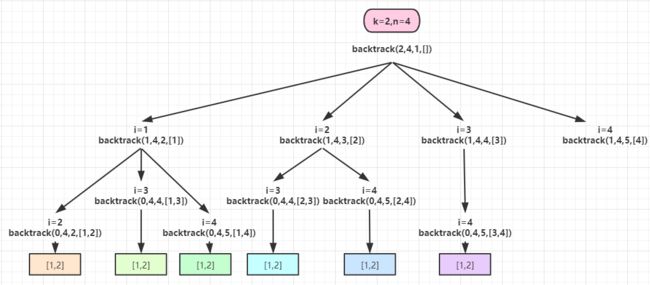
回溯算法,思路如图所示
3、代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
List<Integer> list = new ArrayList<>();
backtrack(n, k, 1, list);
return res;
}
public void backtrack(int n, int k, int start, List<Integer> list){
if(k == 0){
res.add(new ArrayList<>(list));
return;
}
for(int i = start; i <= n; i++){
list.add(i);
backtrack(n, k-1, i+1, list);
list.remove(list.size()-1);
}
}
}
二、Leetcode39. 组合总和
1、题目
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:输入: candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
2、思路
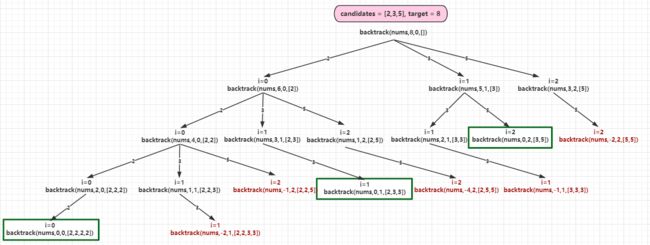
回溯算法,思路如图所示
绿框部分为target=0,满足条件,将list加入结果集,红色部分为剪枝过程,target<0,直接返回,不再向下递归
3、代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<Integer> list = new ArrayList<>();
backtrack(candidates, target, 0, list);
return res;
}
public void backtrack(int[] nums, int target, int start, List<Integer> list){
if(target < 0)
return;
if(target == 0){
res.add(new ArrayList<>(list));
return;
}
for(int i = start; i < nums.length; i++){
list.add(nums[i]);
backtrack(nums, target-nums[i],i, list);
list.remove(list.size()-1);
}
}
}
三、Leetcode40. 组合总和 II
1、题目
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
2、思路
与Leetcode39相似,区别在于39所给数组中无重复元素,元素可重复使用。而此题中数组中有重复元素且一个元素不可重复使用
-
去重
图示:假设相同的数为3 3 [3......3333.....3(第k个3) ] 4 6 7 7 8 9 9 .... p l l+1 r 既然区间[l+1, r]能够求出和为target的组合,其中包含了[l+1, r]区间所有含3的解的情况。 而区间[l, r]3的个数比[l+1, r]3的个数更多,那么毫无疑问,[l, r]的解将覆盖[l+1, r]解中含有3的情况。 因此 if(i!=start && candidates[i] == candidates[i-1]) continue; 此判断语句用来去重 -
元素不可重复使用
下一次递归从
i+1开始
3、代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
List<Integer> list = new ArrayList<>();
backtrack(candidates, target, 0, list);
return res;
}
public void backtrack(int[] candidates, int target, int start, List<Integer> list){
if(target < 0)
return;
if(target == 0){
res.add(new ArrayList<>(list));
return;
}
for(int i = start; i < candidates.length; i++){
if(i!=start && candidates[i] == candidates[i-1]) continue;
list.add(candidates[i]);
backtrack(candidates, target-candidates[i],i+1, list);
list.remove(list.size()-1);
}
}
}
四、Leetcode216. 组合总和 III
1、题目
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
2、思路
- 与前面两题类似,相当于所给数组为[1,2,3,4,5,6,7,8,9]
- 组合中不存在重复的数字,所以递归要从
i+1开始 - 递归终止条件为
list个数达到k且相加之和为n k<0||n<0为剪枝条件,如果满足则返回不再往下递归
- 组合中不存在重复的数字,所以递归要从
3、代码
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
List<Integer> list = new ArrayList<>();
backtrack(k,n,1, list);
return res;
}
public void backtrack(int k, int n, int start, List<Integer> list){
if(k < 0 || n < 0) return;
if(k == 0 && n == 0)
res.add(new ArrayList<>(list));
for(int i = start; i <= 9; i++){
list.add(i);
backtrack(k-1,n-i,i+1, list);
list.remove(list.size()-1);
}
}
}
五、Leetcode377. 组合总和 Ⅳ
1、题目
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3]
target = 4所有可能的组合为:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
2、思路
数据量不大时,如之前一样用回溯算法可以解决
但比如nums = [1, 2, 3],target = 35,最大递归深度达到35,会超出时间限制
一般需要具体求出组合解时用回溯法
只需要求解的个数时,首选动态规划,否则回溯复杂度高,容易超出时间限制
此题顺序不同的序列被视为不同的组合
因此状态转移方程为dp[i] = dp[i-nums[0]]+dp[i-nums[1]]+...dp[i-nums[len-1]],条件为i>=nums[j];
dp[0] = 1,dp[0]表示组成0,一个数都不选就可以了,所以dp[0]=1
举个例子。假设nums={1,2,3}; target = 4
dp[4] = dp[4-1]+dp[4-2]+dp[4-3] = dp[3]+dp[2]+dp[1]
dp[1] = dp[0] = 1;
dp[2] = dp[1]+dp[0] = 2;
dp[3] = dp[2]+dp[1]+dp[0] = 4;
dp[4] = dp[4-1]+dp[4-2]+dp[4-3] = dp[3]+dp[2]+dp[1] = 7
3、代码
/*回溯*/
class Solution {
int res = 0;
public int combinationSum4(int[] nums, int target) {
backtrack(nums, target, 0);
return res;
}
public void backtrack(int[] nums, int target, int start){
if(target < 0){
return;
}
if(target == 0){
res++;
return;
}
for(int i = 0; i < nums.length; i++){
backtrack(nums, target-nums[i], i);
}
}
}
/*动态规划*/
class Solution {
public int combinationSum4(int[] nums, int target) {
if(nums == null || nums.length == 0)
return 0;
int[] dp = new int[target+1];
dp[0] = 1;
for(int i = 0; i <= target; i++){
for(int num : nums){
if(i >= num){
dp[i] += dp[i-num];
}
}
}
return dp[target];
}
}
//顺序不同的序列被视为相同的组合
//遍历nums数组,当前元素有取和不取两种情况dp[i] = dp[i]+dp[i-num]
class Solution {
public int combinationSum4(int[] nums, int target) {
if(nums == null || nums.length == 0)
return 0;
int[] dp = new int[target+1];
dp[0] = 1;
for(int num : nums){
for(int i = 0; i <= target; i++){
if(i >= num){
dp[i] += dp[i-num];
}
}
}
return dp[target];
}
}