数据结构概述(Data structure)

在计算机科学中，数据结构(data structure)是计算机中存储、组织数据的方式。在维基百科中对数据结构是这样形容的：数据结构意味着接口或封装，即一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装。而在百度百科中对数据结构是这么形容的：数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。

目录

1. 数据结构的类型

1.1 线性表(Linear List)

1.1.1 数组

1.1.2 链表

1.1.3 栈

1.1.4 队列

1.2 非线性结构

1.2.1 图结构

1.2.2 树结构

1.2.3 堆

2. 时间复杂度和空间复杂度

2.1 时间复杂度

2.1.1 常数阶

2.1.2 线性阶

2.1.3 平方阶

2.1.4 对数阶

2.1.5 线性对数阶

 2.2 空间复杂度

参考文献：

1. 数据结构的类型

数据结构的类型很多，在python中，有几种内建的集合类型：字符串、列表、字典、元组和集(set)。注意，这里的python中集和上面说的集合不能划等号。python中的集只是具体的一种集合类型。python中的数据结构主要有以下几种：

                                                           

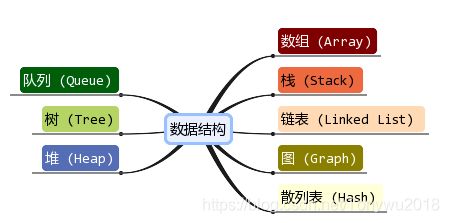
数据结构根据研究对象不同分为数据的逻辑结构和数据的物理结构。

逻辑结构简单说就是数据之间的关系。按数据间关系，逻辑结构可分为两种：线性结构和非线性结构。

线性结构又称线性表，它是一个有限的序列，其中的数据元素之间是一对一的关系，除了首项(只有后继，没有前驱)之外，每一项都有唯一的前驱，除了尾项(只有前驱没有后继)之外，每一项都有唯一的后继。常见的线性结构有：数组(又称顺序表)，栈、队列和链表。

非线性结构就是每一项不止有一个前驱或者后继，常见的非线性结构有：图结构、树结构以及堆。

物理结构是逻辑结构的存储映像。也就是说存储结构是逻辑结构的计算机语言的实现。常见的存储结构有顺序存储、链式存储和散列存储。

顺序存储：把逻辑上相邻的节点存储在物理位置上相邻的存储单元中，节点间的逻辑关系由存储单元的邻接关系来体现。顺序存储通常使用数组来实现。

链式存储：在计算机中用一组任意的存储单元存储线性表的数据元素。各元素在物理上可以不相邻，每个数据元素包括了一个数据域和指针域。链式存储通常使用链表来实现。

散列存储：通过关键字来决定存储的位置，关键字即为索引，不同的关键字对应不同的内容。散列存储通常使用散列表(哈希表)来实现。

根据以上关系，数据结构的框图如下：

         

                   

1.1 线性表(Linear List)

线性表是n个具有相同特性的数据元素的有限序列。线性表中数据元素的关系是一对一的关系。除了首项(只有后继，没有前驱)之外，每一项都有唯一的前驱，除了尾项(只有前驱没有后继)之外，每一项都有唯一的后继。线性表的日常示例有：排队取火车票的人们(先进先出，对应于队列)，一堆排放在桌子上的餐盘(先进后出，对应于栈)。常见的线性表有：数组、链表、栈和队列。

1.1.1 数组

数组又称为线性表，数组在内存中是按顺序存放点的，计算机为数组分配一段连续的内存空间用来存储数据，所以数组中的元素在物理上是连续的。当存储一组数字{1,2,3,4,5}时，其内存空间如下：

                                                     

有关数组的详细内容及python代码实现请参考这篇文章。

1.1.2 链表

引用维基百科中对链表的解释：链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。链表的逻辑顺序和物理单元是解耦的，即链表中的内存单元是非连续的。常见的链表有单向链表、双向链表以及循环链表。用单向链表存储一组数字{1,2,3,4,5}时，其内存空间如下：                                

有关链表的详细内容及python代码实现请参考这篇文章

1.1.3 栈

栈又名堆栈，它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。栈遵循先进后出(First in Last out,FILO)的原则，可以把栈比作堆放到餐桌上的一摞盘子或者手枪的弹夹，往一摞盘子放新的盘子或者往弹夹里装子弹的过程称为压栈；从一摞盘子取走盘子或者子弹从弹夹里打出的过程称为弹栈。用栈存储一组数字{1,2,3,4,5}时，其内存空间如下：

                                                      

有关栈的详细内容及python代码实现我将会在接下来写一篇文章

1.1.4 队列

队列也是一种受限的线性表，队列只允许在后端(rear)进行插入操作，在前端(front)进行删除操作。队列遵循先进先出(First in First out,FIFO)的原则，可以把队列比作排队取票的乘客或者一根两边开口的塑料水管，队列最前面的人取完票离开可以看做是删除元素，新来取票的人只能站在队列的最后端，这可以看做是插入元素。但是我们在买火车票的时候也经常会有军人优先的窗口，这可以看做是优先队列，因为它的优先级别要比普通的窗口优先级别高。用队列存储一组数字{1,2,3,4,5}时，其内存空间如下：

                                                      

有关队列的详细内容及python代码实现我将会在接下来写一篇文章。

1.2 非线性结构

非线性结构就是每一项不止有一个前驱或者后继，常见的非线性结构有：图结构、树结构以及堆。下面逐一简要介绍以上三种数据结构。

1.2.1 图结构

在线性表中说过，线性表中的数据是一对一的关系。而我们知道，数据之间的关系有3种：“一对一”、“一对多”和“多对多”。“一对多”可以通过树结构来实现，而“多对多”就需要通过图结构来进行实现。从数学上讲，图是由顶点(vertice)的集V和边(edge)的集E构成。图的两种常用表示：相邻矩阵(adjacency matrix)和邻接矩阵(adjacency list)。图结构的应用也比较多，比如导航中的路径问题。图的相关概念比较多，有关图的详细内容及python实现我将会专门写一篇文章。无向带标签图的示意图如下：

                                                           

1.2.2 树结构

数据中的3中关系，只剩下了“一对多”，这种数据关系可以由树结构来进行表示。我们日常生活中见到的树是这样的：

                         

而数据结构中的树是把平时看到的树倒过来，“根”在上边，越往下树的结构越庞大。树是由n个有限节点组成的有层次的数据结构。树的相关概念也非常多，同样，有关树的详细内容和python实现我也会专门写一篇文章。一个树结构的简单示意图如下：

                  

1.2.3 堆

堆实际上是一种特殊的树结构，所以它也是一种层级结构且描述数据一对多的关系。有关堆的详细内容，将把它写到树的文章中。此处就不再绘制堆的示意图了。

2. 时间复杂度和空间复杂度

效仿CSDN大神v_JULY_v的爆款博文：理解SVM的三层境界。如果编程也可以分为境界的话，我感觉它可以分为四层境界。
程序的第一层境界也是最基本的准则就是：准确性。这很容易理解，一段程序的基本根源就是它能够准确的运行，至于编码规不规范，程序占用的内存空间以及运行程序所需的时间都不关心，如果把程序类比于人的话，第一层境界意味着这个人是有生命的，他是活着的，至于他的相貌帅不帅，健康不健康，富不富裕都不关心。
程序的第二层境界：鲁棒性。一段程序我们肯定希望它是健壮的，今天能运行，明天运行就会出BUG，或者说在配置运行环境完全一样的另一台计算机上出BUG，这都是程序员最不想看到的。同样的类比于人，第二层境界意味着这个人是健康的，不经常生病，他是在健康的活着。
程序的第三层境界：简洁性和规范性。在完成同样功能的情况下，都希望代码编写的更规范，更简洁，这也能提高代码可读性，不至于将程序交给别人的时候不知道你写的什么；类比与人的话，我想第三层境界应该意味着相貌，代码简洁规范，也就意味着人的颜值高，让人看起来舒服。
程序的第四层境界：performance，也就是性能。对于各种语言，程序基本都是通过顺序语句，判断语句，循环语句这三大语句交叉嵌套实现。那么这一阶段就是考虑怎么能让它性能尽可能的高，性能的高低是通过时间维度和空间维度来考察，时间维度是指当前算法所消耗的时间，通常用时间复杂度来描述；空间维度是指当前算法需要占用的内存空间，通常使用空间复杂度来描述。在这个以数据为原材料的大数据时代，性能尤为重要，因为数量量是巨大的，就拿前段时间观测的黑洞得到的数据量来说，它的数据量需要一万块500G的硬盘来存储，这样巨大的数据量在分析时间和占用内存空间都是巨大的，所以这时候，提高性能，就意味着节省成本。类比与人的话，第四层境界意味着有钱，算法之于程序不是必需的，人没钱同样也可以活着。但是有钱没钱的生活质量是完全不同的，当然也不排除存在像前段时间上海的网红老先生沈魏那样只追求精神层面的人，但是这是极为小众的人群。在这个大数据的时代，数据为本，算法之于程序的追求就如人们解决了温饱追求小康甚至富裕。我想这也是现在为什么算法工程师在IT界如此吃香的原因之一，也是不管你是面前端，面后台，安卓开发，ios开发笔试和面试的时候或多或少都会问到关于算法和数据结构问题的原因之一。

上面也说到performance通过时间复杂度和空间复杂度来衡量，那么是否存在时间复杂度和空间复杂度都比较低的算法呢，实际上这种算法是不存在的，很多时候我们会用时间换空间即通过增加算法的时间运行时间而换得内存的节约或空间换时间即牺牲更多的内存空间而换取更快的算法。时间复杂度和空间复杂度是鱼和熊掌不可兼得的问题，所以，我们要找到二者的平衡点。

2.1 时间复杂度

那么我们该如何度量时间代价呢，有人说我们可以导入time模块，在程序执行前获取当前时间，在程序末尾再次获取当前时间，两者做差，即可求出运行该算法所需要的时间。

import time               # 导入time模块
start = time.time()       # 获取当前时间戳
pass                      # 要执行的程序代码
end = time.time()         # 获取当前时间戳
runTime = end - start     # 获取程序运行时间

当然也有很多编译器像sublime会直接给出运行这段程序所需要的时间，而不需要我们人为的去做计算。 比如我们在执行下面语句的时候，就会在console显示运行时间。

         

这是一个办法，但是并不是一个好办法。因为不同的计算机配置，运行程序所需要的时间显然是不一样的；同样的算法应用于不同数据量的数据，其运行时间也是不一样的。这就不能单纯的根据程序运行时间来衡量时间复杂度了。算法的时间复杂度通常用大O表示法来描述，表示为：T(n) = O(f(n))。

我们从常见的时间复杂度量级来对大O表示法进行理解：常数阶、线性阶、平方阶、对数阶，常数对数阶。当然还有指数阶和立方阶等，但是这些量级的时间复杂度用的不是特别多，所以不对其进行说明。下面是时间复杂度不同量级的线性图。

                                        

假设有如下的代码：

ls = []
for i in range(n):
    ls.append(i)
print(ls)

假设执行每行代码所需要的时间是一样的，我们认为执行一行代码花费一个单位时间，那么上面的代码中，第一行代码花费了1个单位时间，第二行花费了1个单位时间，第三行被执行了n次，每一次花费一个单位时间，那么第三行花费了n个单位时间，第四行也花费了1个单位时间。那么执行上述代码花费了n+3个单位时间，我们只考虑主项，很明显，主项是n，当n比较大时常数项3(或者100,1000)可以被忽略，所以上述代码的时间复杂度是。同样的，如果代码执行时间为：，那么其主项就是，所以代码的时间复杂度可以看做是。所以时间复杂度并不是程序运行的具体时间。 通过几段小程序分别对几种不同量级的时间复杂度进行分析。

2.1.1 常数阶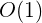

一段程序无论有多少行，只要它没有循环，我们就可以认为时间复杂度是常数阶的。

  

上述代码实现了交换a,b的值，一共有5行，它的时间复杂度是常数阶。实际上python中实现交换两个数只需3行代码即可搞定。如下：

   

2.1.2 线性阶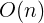

上面的将n个数添加到列表中的程序段的时间复杂度就是线性阶的，以对1-n求和为例：

          

上述代码的时间复杂度就是线性阶，数据规模n和花费单位时间成比例，n为10，花费14个单位时间，n为100花费104个单位时间，n为1000花费1004个单位时间，用多项式表示就是n+4，所以其线性复杂度为

2.1.3 平方阶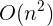

 当嵌套2层for循环时，算法的时间复杂度就变成了平方阶，以冒泡排序为例对其进行说明：

 关于冒泡排序的图解如下：

选择排序的时间复杂度不受输入数据的影响，其时间复杂度一直都是，其代码如下：

关于选择排序的图解如下：

2.1.4 对数阶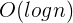

对数阶比线性阶好一些，比常数阶差一些。对数阶的算法工作量和数据规模的成比例。所以当数据的规模翻倍时，其工作量只增加1。以二叉搜索(二分查找)为例，对对数阶复杂度进行分析。

可以看到上述代码只有一个循环，理论上气复杂度应该是线性阶，但是right和left是进行了倍缩或倍增，假设数据规模为16的话，那么二分查找最多只进行4次搜索操作即可找到目标值。所以其时间复杂度为：，所以二分查找的时间复杂度是对数阶的。

关于二分查找的图解如下：

 

2.1.5 线性对数阶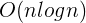

线性对数阶就是在对数阶的基础上增加一个线性。实际上在对数阶算法上加一个for循环即可。典型的线性对数阶的算法有快速排序、归并排序等。以快速排序为例，对线性对数阶复杂度进行说明：

上述代码中的第61和62行使用了列表生成式。其中第61行代码与以下代码等效：

left = []
for i in range(1,len(nums)):
    if nums[i] < pivot:
        left.append(nums[i])

 2.2 空间复杂度

一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度，可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分：

(1) 固定部分，这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。

(2) 可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。

一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))，其中n为问题的规模，S(n)表示空间复杂度。

空间复杂度可以理解为除了原始序列大小的内存，在算法过程中用到的额外的存储空间。

参考文献：

1. 维基百科：数据结构             https://zh.wikipedia.org/wiki/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84

2. 百度百科：数据结构             https://baike.baidu.com/item/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84/1450

3. 数据结构，物理结构，存储结构和逻辑结构的区分     https://www.cnblogs.com/Xieyang-blog/p/8516113.html

4. 数据结构概述                       http://data.biancheng.net/intro/

5. 维基百科：链表                    https://zh.wikipedia.org/wiki/%E9%93%BE%E8%A1%A8

6. 解读算法「时间」与「空间」复杂度——冰与火之歌         https://mp.weixin.qq.com/s/vncb5vu4ykj-LeGB0T8Qqw