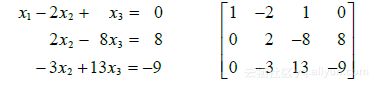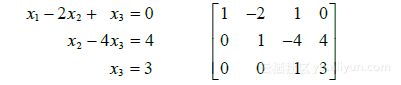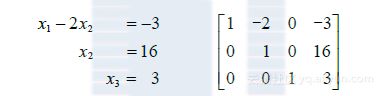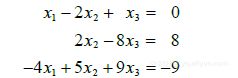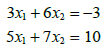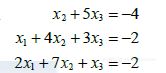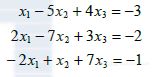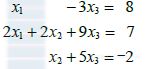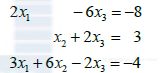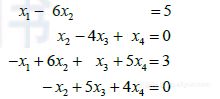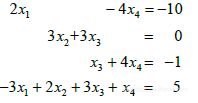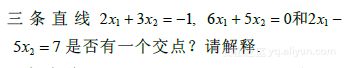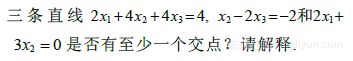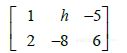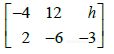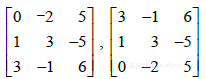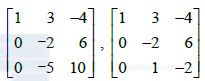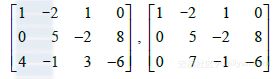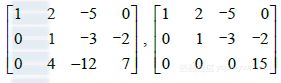《 线性代数及其应用 （原书第4版）》—— 第1章 线性代数中的线性方程组1.1 线性方程组...
本节书摘来自华章出版社《 线性代数及其应用 （原书第4版）》一书中的第1章，第1.1节，作者:（美）戴维C. 雷（David C. Lay）马里兰大学帕克学院 著刘深泉 张万芹 陈玉珍 包乐娥 陆 博 译，更多章节内容可以访问云栖社区“华章计算机”公众号查看
第1章 线性代数中的线性方程组
介绍性实例 经济学与工程中的线性模型
1949年夏末，哈佛大学教授列昂惕夫（Wassily Leontief）正在小心地将最后一部分穿孔卡片插入大学的MarkⅡ计算机. 这些卡片包含了美国经济的信息，包括了美国劳动统计局两年紧张工作所得到的总共25万多条信息. 列昂惕夫把美国经济分解为500个部门，例如煤炭工业、汽车工业、交通系统等等. 对每个部门，他写出了一个描述该部门的产出如何分配给其他经济部门的线性方程. 由于当时最大的计算机之一的MarkⅡ还不能处理所得到的包含500个未知数的500个方程的方程组，列昂惕夫只好把问题简化为包含42个未知数的42个方程的方程组.
为解列昂惕夫的42个方程，编写MarkⅡ计算机上的程序需要几个月的工作，他急于知道计算机解这个问题需要多长时间. MarkⅡ计算机运算了56个小时，才得到最后的答案. 我们将在1.6节和2.6节中讨论这个解的性质.
列昂惕夫获得了1973年诺贝尔经济学奖，他打开了研究经济数学模型的新时代的大门. 1949年在哈佛的工作标志着应用计算机分析大规模数学模型的开始. 从那以后，许多其他领域中的研究者应用计算机来分析数学模型. 由于所涉及的数据数量庞大，这些模型通常是线性的，即它们是用线性方程组描述的.
线性代数在应用中的重要性随着计算机功能的增大而迅速增加，而每一代新的硬件和软件引发了对计算机能力的更大需求. 因此，计算机科学就通过并行处理和大规模计算的爆炸性增长与线性代数密切联系在一起.
科学家和工程师正在研究大量极其复杂的问题，这在几十年前是不可想象的. 今天，线性代数对许多科学技术和工商领域中的学生的重要性可说超过了大学其他数学课程. 本书中的材料是在许多有趣领域中进一步研究的基础. 这里举出几个例子，以后将列举其他一些领域.
.石油探测. 当勘探船寻找海底石油储藏时，它的计算机每天要解几千个线性方程组. 方程组的地震数据从气喷枪的爆炸引起水下冲击波获得. 这些冲击波引起海底岩石的震动，并用几英里长的电缆拖在船后的地震测波器采集数据.
. 线性规划. 许多重要的管理决策是在线性规划模型的基础上作出的，这些模型包含几百个变量，例如，航运业使用线性规划调度航班、监视飞机的飞行位置，或计划维修和机场运作.
. 电路. 工程师使用仿真软件来设计电路和微芯片，它们包含数百万的晶体管. 这样的软件技术依赖于线性代数与线性方程组的方法.
线性方程组是线性代数的核心，本章使用它来引入线性代数的许多重要概念. 1.1节和1.2节介绍求解线性方程组的一个系统方法，这个算法在全书的计算中都用到. 1.3节和1.4节指出线性方程组等价于一个向量方程与矩阵方程. 这种等价性把向量的线性组合问题化为线性方程组的问题. 线性表示，线性无关和线性变换的基本概念将在本章后半部分研究，它们在整本书中起着关键的作用，并使我们体会到线性代数的魅力和威力.
1.1 线性方程组
包含未知数 的一个线性方程是形如
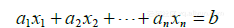 （1）的方程，其中b与系数 
是实数或复数，通常是已知数. 下标n可以是任意正整数. 在本书的例题中，n通常是在2与5之间. 在实际问题中，n可以是50，5000或更大.
方程
都是线性方程，因为它们可以化为
方程
都不是线性方程，因为第一个方程中包含
，第二个方程中包含
.线性方程组是由一个或几个包含相同变量
的线性方程组成的. 例如，
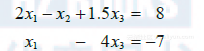 （2）线性方程组的一组解是一组数
，用这组数分别代替 
时所有方程的两边相等. 例如，方程组（2）有一组解(5，6.5，3)，这是因为，在（2）中用这些值代替 
时，方程组变成等式8=8和 -7=-7.
方程组所有可能的解的集合称为线性方程组的解集. 若两个线性方程组有相同的解集，则这两个线性方程组称为等价的. 也就是说，第一个方程组的每个解都是第二个方程组的解，第二方程组的每个解都是第一方程组的解.
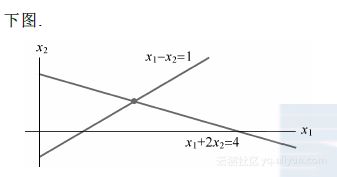
求包含两个未知数的两个方程组成的方程组的解，等价于求两条直线的交点. 一个典型的例子是
这两个方程的图形都是直线，分别用l1和l2表示，数对
满足这两个方程当且仅当点 是这两条直线的交点. 容易验证，这个方程组有唯一的解(3，2)，如图1-1所示.
当然，两条直线不一定交于一个点，它们可能平行，也可能重合，重合的两条直线上的每个点都是交点. 图1-2是与下面两个方程组对应的图形：
图1-1和图1-2说明线性方程组的下列一般事实，这将在1.2节证明.
线性方程组的解有下列三种情况：
- 无解.
- 有唯一解.
- 有无穷多解.
我们称一个线性方程组是相容的，若它有一个解或无穷多个解；称它是不相容的，若它无解.
图1-1 有唯一解
a）无解 b）无穷多解
图 1-2
矩阵记号
一个线性方程组包含的主要信息可以用一个称为矩阵的紧凑的矩形阵列表示. 给出方程组
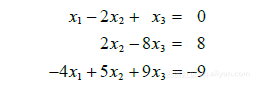（3）把每一个变量的系数写在对齐的一列中，矩阵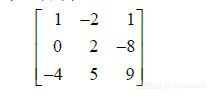
称为方程组（3）的系数矩阵，而
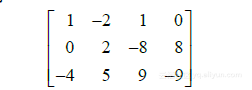 （4）称为它的增广矩阵.（第二行第一个元素为0，因第二个方程可写成 
）方程组的增广矩阵是把它的系数矩阵添上一列所得，这一列是由方程组右边常数组成的.
矩阵的维数说明它包含的行数和列数. 上面的增广矩阵（4）有3行4列，称为3x4（读作3行4列）矩阵. 若m, n是正整数，一个m x n矩阵是一个有m行n列的数的矩形阵列.（行数写在前面.）矩阵记号为解方程组带来方便.
线性方程组的解法
本节和下一部分给出了解线性方程组的一般方法. 基本的思路是把方程组用一个更容易解的等价方程组（即有相同解集的方程组）代替.
粗略地说，我们用方程组中第一个方程中含x1的项消去其他方程中的含x1的项. 然后用第二个方程中含x2的项消去其他方程中含x2的项，依此类推. 最后我们得到一个很简单的等价方程组.
用来化简线性方程组的三种基本变换：把某一个方程换成它与另一方程的倍数的和；交换两个方程的位置；把某一方程的所有的项乘以一个非零常数. 在例1之后，我们将说明经过这三种变换，为什么不改变方程组的解集.
例1 解方程组（3）.
解 我们在消去未知数的同时用方程组与相应的矩阵形式表示出来以便比较.
保留第一个方程中的x1，把其他方程中的x1消去. 为此，把第1个方程乘以4，加到第3个方程上. 熟练之后可以通过心算完成：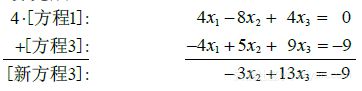
把原来的第三个方程用所得新方程代替：
其次，把方程2乘以1/2，使x2的系数变成1.
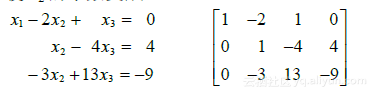
利用方程2中的x^2项消去方程3中的项-3x^2 ，用心算计算如下：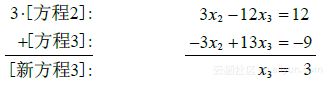
所得的新方程组有三角形形状：
现在我们想消去第一个方程中的项 ，不过先利用方程3消去第一个方程中的项x3和第二个方程中的项 更为有效. 这两个运算如下：
这两次变换的结果如下：
现在，在x3的一列中只剩一项，我们回头来消去第一个方程中的x2项. 把方程2的2倍加到方程1，得到方程组：
我们已经得出结果：原方程组的唯一解是(29, 16, 3)，我们做了这么多计算，最好还是检验一下结果. 为证明(29, 16, 3)是方程组的解，把这些值代入原方程组的左边：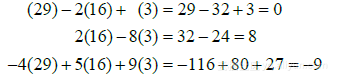
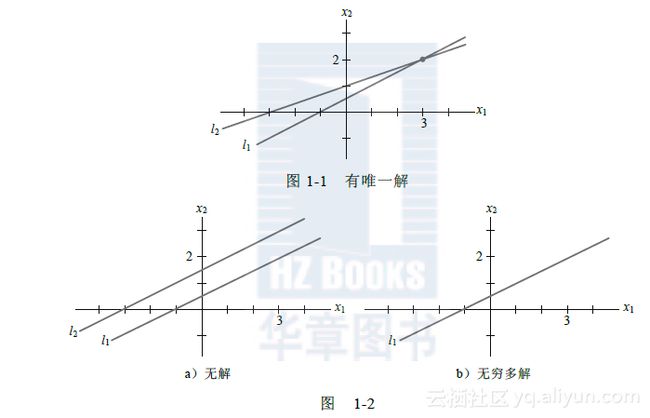
结果与原方程组右边相同，所以(29, 16, 3)是原方程组的解（见图1-3）.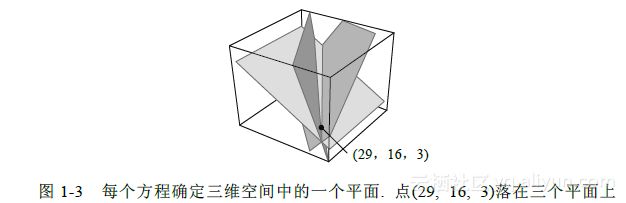
例1说明了线性方程的变换对应于增广矩阵的行的变换. 前面所讲的三种基本变换对应于增广矩阵的下列变换.
行初等变换
1.（倍加变换）把某一行换成它本身与另一行的倍数的和.
2.（对换变换）把两行对换.
3.（倍乘变换）把某一行的所有元素乘以同一个非零数.
行变换可施行于任何矩阵，不仅是对于线性方程组的增广矩阵. 我们称两个矩阵为行等价的，若其中一个矩阵可以经一系列行初等变换成为另一个矩阵.
重要的一点是行变换是可逆的. 若两行被对换，则再次对换它们就会还原为原来的状态. 若某一行乘以非零常数c，则将所得的行乘以 就得出原来的行. 最后，考虑涉及两行的倍加变换，例如第一行和第二行. 假设把第一行的c倍加到第二行得到新的第二行，那么“逆”变换就是把第一行的-c倍加到（新的）第二行上就得到原来的第二行. 见本节末习题29~32.
此时，我们更关注对一个线性方程组的增广矩阵进行行变换. 假设一个线性方程组经过行变换变成另一个新的方程组，考虑每一种行变换，容易看出，原方程组的任何一个解仍是新的方程组的一个解. 反之，因原方程组也可由新方程组经行变换得出，新方程组的每个解也是原方程组的解. 这就证明了下列事实.
若两个线性方程组的增广矩阵是行等价的，则它们具有相同的解集.
虽然例1看起来很长，经过一些练习你还是可以很快掌握的. 本书中习题的行变换通常是很简单的，因而你可以集中精力理解其中的思想和概念. 当然你必须熟练掌握这些变换，因为整本书都要用到它们.
本节的其他部分将介绍如何利用行变换来确定解集的情况，而无须完全求出解来.
存在与唯一性问题
在1.2节中我们将会知道，为什么一个线性方程组的解集可能不包含任何解、一个解或无穷多个解. 为确定某个方程组属于哪种情况，我们提出以下两个问题.
线性方程组的两个基本问题
- 方程组是否相容，即它是否至少有一个解？
- 若它有解，它是否只有一个解，即解是否唯一？
这两个问题将在整本书中以各种形式出现. 本节与下节中，我们将说明如何通过增广矩阵的行变换来回答这些问题.
例2 确定下列方程组是否有解
解 这就是例1中的方程组. 设我们已把方程组通过行变换变成三角形
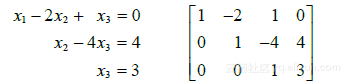
这时我们已经确定了x3，若把x3的值代入方程2，我们就会确定x2，因而可由方程1确定x1，所以解是存在的，即该方程组是相容的.（事实上，x2由方程2唯一确定，而x1由方程1唯一确定，所以解是唯一的.）
例3 确定下列方程组是否相容：
 （5）解 增广矩阵为：
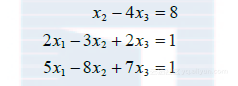为使第一个方程包含x1项，对换第一行与第二行：
为消去第3个方程的项 ，把第1行的?5/2倍加到第3行：
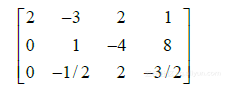 （6）其次，用第二个方程的x2项消去第三个方程的 项，把第2行的1/2倍加到第3行上：
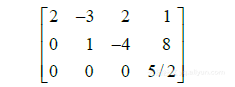（7）现在增广矩阵已成为三角形，我们来说明这个矩阵. 化为方程表示：
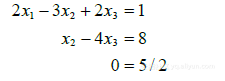 （8）方程0-5/2是 的简写. 这个三角形线性方程组显然是矛盾的，所以满足（8）的未知数 的值是不可能存在的，因等式0-5/2不可能成立. 由于（8）和（5）有同样的解集，原方程组是不相容的（即无解），见图1-4.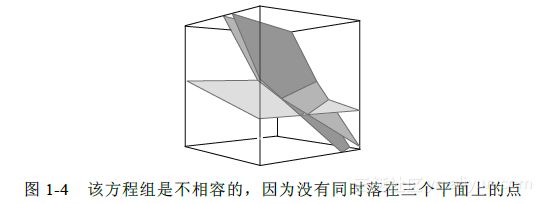
图1-4 该方程组是不相容的，因为没有同时落在三个平面上的点
注意（7）的增广矩阵，它的最后一行在三角形不相容方程组中是典型的.
数值计算的注解 在实际问题中线性方程组是通过计算机求解的. 对于方阵，计算机程序基本上是应用这里以及1.2节的消去法，稍做修正以改进精确度.
工商业中的大量线性代数问题运用浮点运算求解，数表示为小数形式： ，r是整数，而小数点右面的数位为8至16位. 这种数的算术运算一般是有误差的. 其结果必须四舍五入（或舍去）为存储时需要的数位.“舍入误差”在输入像1/3这样的数时也会产生，因为它必须用近似的有限位小数表示. 幸运的是，浮点运算中的不精确性很少引起严重问题. 本书中关于数值计算的注解将会提醒你注意这些问题.
练习题
本书中练习题应该在做习题之前完成，它们的解答在每一节习题之后给出.
-
用语言叙述解每个方程组时下一步应做的行变换.
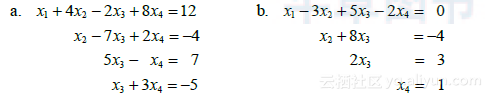 - 某线性方程组的增广矩阵已经由行变换化为以下形式. 确定它是否有解.
- 数组(3，4，?2)是否为下列方程组的解：
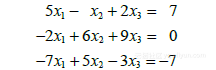
- 当h和k取何值时下列方程组相容？
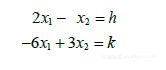
习题1.1
利用对方程或增广矩阵的行初等变换解1-4题中的方程组. 依照本节中给出的消去过程.
- 求在直线 上的点 ，见下图.
- 求直线
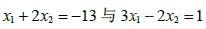
的交点.
习题5、6中的矩阵是某个线性方程组的增广矩阵. 说明在解方程组时下一步应进行的行初等变换.
在7~10题中某个线性方程组的增广矩阵已由行变换化成如下所示，继续进行适当的行变换并说明原方程组的解集.
解11~14题的方程组：
确定15~16题中的方程组是否相容，不必解出方程组.
18.
在19~22题中，确定h的值使矩阵是某一个相容方程组的增广矩阵：
在23~24题中，或是直接引用本节的重要命题，略为改述（但依然成立），或被错误修改. 判断每个命题的真或假并给出理由. （若判断为真，指出教材中相似命题的出处，或参考的定义、定理. 若判断为假，指出引用或用错的命题出处，或举例说明.）类似的真/假问题会在本教材的许多章节中出现.
-
- 两个矩阵是行等价的，若它们有相同的行数.
- 对增广矩阵的行初等变换不改变相关的线性方程组的解集.
- 两个线性方程组是等价的，若它们有相同的解集.
- 不相容线性方程组有一个或更多解.
- 求出包含g，h和k的方程组，使以下矩阵是相容方程组的增广矩阵.
- 设下面的方程组对所有f和g的可能取值都是相容的，则系数c和d有何特性？给出理由.
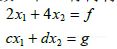
- 设 为常数，a不为零，下面的方程组对所有f和g的可能取值都是相容的，则系数 有何特性？给出理由.
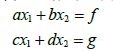
- 给解集为
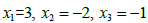
的线性方程组构造三个不同的增广矩阵.
在29~32题中，求出把第一个矩阵变为第二个矩阵的行初等变换，并求出把第二个矩阵变为第一个矩阵的逆行初等变换.
热传导的研究中，重要问题是确定某一块平板的稳态温度分布，假设已知边界上的温度分布，假设下图中的平板代表一条金属梁的截面，忽略垂直于该截面方向上的热传导，设 表示图中4个内部结点的温度. 某一节点的温度近似地等于4个与它最接近的结点（上、下、左、右）的平均值 ，1例如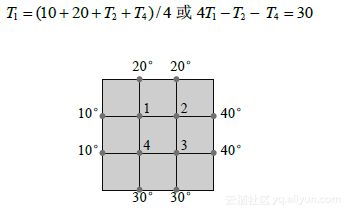
- 写出温度
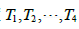所满足的方程组. - 解习题33中写出的方程组.（提示：为快速计算，在对换变换之前先对换第1行和第4行.）
练习题答案
-
- 手工计算时，最好是把方程3与4对换，另一种办法是把方程3乘以1/5，或把方程4化为它与方程3的-1/5倍的和（不要利用方程2中的
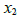项消去方程1中 
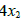，而要等到得到三角形矩阵且
项已从前2个方程消去之后）.
- 手工计算时，最好是把方程3与4对换，另一种办法是把方程3乘以1/5，或把方程4化为它与方程3的-1/5倍的和（不要利用方程2中的
- 方程组已是三角形. 进一步的简化可利用第四个方程中的
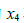项消去它上面的各个 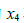项，现在适当的步骤是把方程4的2倍加到方程1上（此后再把方程3乘以1/2，再消去其他的
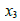项）. - 对应于该增广矩阵的方程组是
由第三个方程得到 ，这当然是允许的. 消去前两个方程中的 项，我们可以继续求出方程组的唯一解. 因此解是存在且唯一的. 注意比较本题与例3.
3.
4.