我们首先来看一下什么是前向星.
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,
并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.
用len[i]来记录所有以i为起点的边在数组中的存储长度.
用head[i]记录以i为边集在数组中的第一个存储位置.
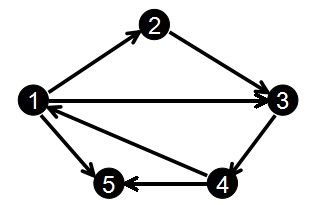
那么对于下图:
我们输入边的顺序为:
1 2
2 3
3 4
1 3
4 1
1 5
4 5
那么排完序后就得到:
编号: 1 2 3 4 5 6 7
起点u: 1 1 1 2 3 4 4
终点v: 2 3 5 3 4 1 5
得到:
head[1] = 1 len[1] = 3
head[2] = 4 len[2] = 1
head[3] = 5 len[3] = 1
head[4] = 6 len[4] = 2
但是利用前向星会有排序操作,如果用快排时间至少为O(nlog(n))
如果用链式前向星,就可以避免排序.
我们建立边结构体为:
struct Edge
{
int next;
int to;
int w;};
其中edge[i].to表示第i条边的终点,edge[i].next表示与第i条边同起点的下一条边的存储位置,edge[i].w为边权值.
另外还有一个数组head[],它是用来表示以i为起点的第一条边存储的位置,实际上你会发现这里的第一条边存储的位置其实
在以i为起点的所有边的最后输入的那个编号.
head[]数组一般初始化为-1,对于加边的add函数是这样的:
void add(int u,int v,int w)
{
edge[cnt].w = w;
edge[cnt].to = v;
edge[cnt].next = head[u];
head[u] = cnt++;
}初始化cnt = 0,这样,现在我们还是按照上面的图和输入来模拟一下:
edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;
很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.
这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.
比如以上图为例,以节点1为起点的边有3条,它们的编号分别是0,3,5 而head[1] = 5
我们在遍历以u节点为起始位置的所有边的时候是这样的:
for(int i=head[u];~i;i=edge[i].next)
那么就是说先遍历编号为5的边,也就是head[1],然后就是edge[5].next,也就是编号3的边,然后继续edge[3].next,也
就是编号0的边,可以看出是逆序的.
【存储】浅谈链式前向星
链式前向星是一种相当有效的存储方式,是一种静态的链表式存储,将前向星改写为链式前向星可以避免排序带来的复杂度(普通前向星需要排序,一般选用基数排序),以下开始讨论链式前向星。
在本文中,除非特别注明,我们都以下图作为讨论的基本依据:对于这个图而言,有一输入顺序如下:
1 2
2 3
3 4
1 3
4 1
1 5
4 5首先,我们先提出链式前向星的基本结构:
struct Edge2
{
int to;
int next;
int w;
};
Edge2 Edge[maxn];对于next:
如果一个结点的出度大于1,则其中结点编号最大的结点的next将指向结点编号次之的结点。举个例子,从结点1出发,结点编号最大的是结点5,结点5的next将会是3,而结点3的next将会是结点2,而到了结点2之后结点1的所有出边都已经被处理了,所有结点2的next将会是-1,这样子将可以找到对于结点1的所有直接相接的结点(注意:遍历时结点是由大到小遍历的,即是逆序的)。当检测到next的值为-1时会退出当前遍历。
如果结点的出度为0或者小于1,则对应的next值为-1。推荐用笔在纸上模拟一次这个过程,模拟过程的数据可以在该文章后面一些的地方找到。对于to:
简单概括来说就是对于第i条边的终点,比如说输入第一组边(1, 2)的时候,Edge[0].to = 2(数组从0开始存储)。
这里有一个要注意的点,如果是有向图,那么只要处理一次就够了。对于一个无向图的话,就需要来回存一次,对于无向图的具体存法可以看文末给出的题目和相关代码。对于weight:
很明显这个就是用来存边的权重的一个变量,这里不再多讨论。
然后,我们还需要一个head数组,这个head数组和next是这个链式存储结构的关键所在!
那么这个head数组用来存什么呢?对于你输入的边,用来存以i为起点的边的存储位置。那么如果以i为起点的边出度大于1怎么办?此时head[i]会存入在输入中最后输入的以i为起点的编号。比如说对于结点1,它的出度为3,由先往后分别输入了(1, 2)(1, 3)(1, 5),最后存入head的就会是5(2和3其实也有被存储的时候,但是后来会被5覆盖掉),即结果就是head[1] = 5。对于输入的边的存储方式如下:
void Build(int u, int v, int w){
Edge[k].to = v;
Edge[k].weight = w;
Edge[k].next = head[u];
head[u] = k++;
} 这个读入的过程同样推荐用笔算一次,可以很好的帮助理解。这里提一下关于head[u]的问题,以以1为起点的边为例子,第一次读入(1,2)的时候,很明显,head[u] = -1的,即head[1] = -1。那么下面的head[u]又是干什么的呢?还是以“以1为起点的边”作为例子,(1, 2)的时候,head[1] = -1;然后在“head[u] = k++”这一行把这个值记录下来,简单来说就是u这个值在第几组输入的边里出现过,放到这个例子里就是head[1] = 0;而后,读入(1,3)(1,5)的时候, head[1]的值会再次被刷新,最后得出的head[1] = 5。样例数据:
edge[0].to = 2; edge[0].next = -1; head[1] = 0;
edge[1].to = 3; edge[1].next = -1; head[2] = 1;
edge[2].to = 4; edge[2],next = -1; head[3] = 2;
edge[3].to = 3; edge[3].next = 0; head[1] = 3;
edge[4].to = 1; edge[4].next = -1; head[4] = 4;
edge[5].to = 5; edge[5].next = 3; head[1] = 5;
edge[6].to = 5; edge[6].next = 4; head[4] = 6;那么它是怎么进行遍历的呢?这里我们以Luogu2420作为例子:
void solve(int num){
for(int i = head[num]; i != -1; i = Edge[i].next)
if(!visit[Edge[i].start])
{
visit[Edge[i].start] = true;
dis[Edge[i].start] = dis[num]^Edge[i].weight;
solve(Edge[i].start);
}
}主要分两块,一块就是循环体,一块是递归体。
转回上文中有向图的实例,循环的主要作用就是对拥有同一起点的边进行跳转(比如说从(1,5)转到(1, 3)再转到(1, 2),就是我前文所写的next的作用,相当于一个静态的链表),而递归体主要就是DFS(比如说从(1, 3)到(3, 4)再到(4, 5)再到(4, 1),这里同样推荐用笔写一写,会清晰很多)。这样子我们就成功使用链式前向星来存下了一个图,并能够对它进行遍历。
然后也有一道不错的题可以用链式前向星来做,比如上文提到的Luogu2420(其实我就是因为这道题才知道这个的...),可以去做一下,代码放在另一篇博文里,这里就不多提及了。参考资料:
https://blog.csdn.net/m0_37389559/article/details/75200652
https://malash.me/200910/linked-forward-star/
题目链接:
https://www.luogu.org/problemnew/show/P2420
代码链接:
https://oi-liu.com/2018/04/20/p2420