论文《Neural Collaborative Filtering》阅读

论文概况

论文《Neural Collaborative Filtering》是由新加坡国立大学何向南教授完成的一篇关于基于神经网络方法的推荐系统论文，发表在WWW 2017上，CCF A。
论文地址：NeuMF
数据集：MovieLens、Pinterest
代码地址：NeuMF

论文亮点

这篇文章使用神经网络（NN, Neural Network）方法完成了推荐系统中的协同过滤，不同于其他算法中使用神经网络提取辅助特征，user和item仍然使用矩阵内积来计算；这篇文章使用神经网络直接计算user和item之间的关系，并通过神经网络（1）来代替矩阵分解算法（形成模型GMF）来提取user和item之间的线性关系，（2）搭建3层的MLP来提取user和item之间的非线性关系，（3）组合MLP和GMF形成最终的NeuMF模型。

文章的主要部分按照论文的顺序进行介绍。

Introduction

推荐系统中主流方法是协同过滤CF（Collaborative Filtering）方法，协同过滤中最流行的就是矩阵分解MF（Matrix Factorization）算法。但是矩阵分解算法由于在隐空间中只是将user和item的矩阵进行简单内积运算，由此导致了很大程度的信息丢失。

这里我举例说明一下，对于矩阵$U\in {\mathbb{R}}^{m\times k}$和矩阵$V\in {\mathbb{R}}^{k\times n}$，矩阵相乘，在结果矩阵$R\in {\mathbb{R}}^{m\times n}$每个位置得到的结果$R_{ij}$相当于左矩阵$U$的每一行$u_i^{\mathsf{T}}$与右矩阵的每一列$v_j$内积运算的结果：$R_{ij}=<u_i,v_j>=u_i^{\mathsf{T}}\cdot v_j$。

由此进行拓展，对于矩阵分解算法，每一个$R_{ij}$其实就是$u_i$和$v_j$对应位置线性相乘之和。对于这种线性运算，我们在机器学习关于多层神经网络为什么要加入激活函数那里应该多次学习过非线性运算的重要性，这里不再赘述。

所以作者提出将简单的矩阵相乘改由深层神经网络模型解决的思路，并指出以往的深度学习方法大多是在辅助信息（Auxiliary Information）上整活儿，但是这篇文章是直接将向量内积的部分改掉。

Preliminaries

implicit data的推荐问题

作者介绍了impllcit feedback的定义，这部分在我们之前的推荐系统论文阅读中已经多次介绍，这里不再赘述。这里介绍point-wise loss和pairwise loss的区别。给定$y_{ui}$，point-wise loss致力于缩小每一个$y_{ui}$和${\hat{y}}_{ui}$之间的距离，这样做的前提是认为用户不喜欢每个$y_{ui}=0$的item，但这是不对的（和我们日常经验保持一致，我们去超市买东西，买到的东西认为我们喜欢这没问题，但是没买到的东西都是不喜欢的这就问题太大了，因为更常见的情况是我们没买只是因为我们不知道这个东西的存在）;pair-wise loss则假定一个排序，认为和user有互动的item比没有互动的item优先级更高，我们应该拉大两者之间的距离。

Matrix Factorization

这里作者举了一个例子来证明矩阵分解算法的局限性。作者首先将矩阵分解是线性运算进行了解释，也就是我们在Introduction中说明的内容，公式化如下：
$${\hat{y}}_{ui}=f(u,i|p_u,q_i)=p_u^{\mathsf{T}}{q}_i=\sum _{k=1}^K{p}_{uk}{q}_{ik}$$
这里的大写$K$表示隐空间维度。

这里作者用上图来说明即使实际中看起来更相似（Jaccard系数更近）的两个向量，在坐标系中的内积并不一定更小（单位向量的夹角不一定更小）。但是我个人并不认同这个例子，这个例子很大程度上是用结论去证明假设，给人本末倒置的感觉。举例来说，如果$p_1$放到$p_3$的相反方向，同时保持两个$p_4$和$p_1$的相对位置不变，同样可以表达$p_1$离$p_2$的距离小于$p_1$和$p_3$间的距离的同时却依然有$p_4$与$p_2$夹角小于$p_4$与$p_3$夹角的事实。

另外，这里说明一下，论文中关于Jaccard系数的公式应该有笔误，将交兵符号放到了集合大小符号外面，应该如下：
$$S_{ij}=\frac{|R_i\cap R_j|}{|R_i\cup R_j|}$$

关于这两两点问题，欢迎评论区讨论和指教。

神经协同过滤算法

这一节介绍文章的核心算法部分。

通用框架

下图2展示了本文的通用神经网络框架，我们逐层进行介绍。

• Input Layer：最下层的两个输入分别表示user和item，分别使用user和item的编号的one-hot编码格式作为输入向量。
• Embedding Layer：全连接层，将one-hot编码转换为一个较短的向量形式。
• Neural CF Layers：神经协同过滤层，包含多层，本文使用三层的格式，每层神经元个数减半，全连接前馈神经网络形式。
• Output Layer：最终输出只有一个值，离1越近表示user可能越喜欢这个item。与${\hat{y}}_{ui}$进行比较后，将损失进行反向传播，优化整个模型。

下面我们介绍网络细节。

首先，针对输入层，作者表示可以使用其他embedding作为输入，如基于上下文的特征向量、基于内容的特征向量、基于邻居节点的特征向量等。本文使用编号的one-hot编码向量作为输入是因为如果将embedding层的矩阵 $P$ 和 $Q$ 看作是我们在矩阵分解算法中的潜因子矩阵的话，则通过user $u$ 的one-hot向量与之相乘，得到的正好是user $u$ 对应的那一行$P_u$，itme矩阵同理，这样就可以很好地进行对矩阵分解的模拟。同时作者指出，使用one-hot编码可以很好地解决推荐系统中的冷启动问题。

神经协同过滤层的最后一层，也就是最接近输出层的那一层包含的神经元个数$X$，作者将其称之为预测因子（predictive factor），预测因子越大，模型的描述能力就越强，但是预测因子过大，则可能带来过拟合。

模型形式化描述如下：
$${\hat{y}}_{ui}=f(P^{\mathsf{T}}{v}_u^{\mathsf{U}},Q^{\mathsf{T}}{v}_i^{\mathsf{I}}|P,Q,{\Theta }_f)\text{\hspace{1em}(3)}$$

如公式3所示，$P\in {\mathbb{R}}^{M\times K}$， $Q\in {\mathbb{R}}^{N\times K}$分别用来表示user和item的潜因子矩阵（latent factor matrix）。公式3表示给定$P,Q,{\Theta }_f$，根据映射完成的user embedding和item embedding完成交互分数的预测。针对多层神经网络而言，上式可以进一步表示为：
$$f(P^{\mathsf{T}}{v}_u^{\mathsf{U}},Q^{\mathsf{T}}{v}_i^{\mathsf{I}})={\varphi }_{out}({\varphi }_X(\cdots {\varphi }_2({\varphi }_1(P^{\mathsf{T}}{v}_u^{\mathsf{U}},Q^{\mathsf{T}}{v}_i^{\mathsf{I}}))\cdots ))\text{\hspace{1em}(4)}$$

NCF学习

常用的平方差损失函数如下：
$$L_{sqr}=\sum _{(u,i)\in \mathcal{Y}\cup {\mathcal{Y}}^{-}}{\omega }_{ui}(y_{ui}-{\hat{y}}_{ui}{)}^2\text{\hspace{1em}(5)}$$

这里的平方差损失函数是将所有的互动分数（包括user没有观察到的item）全部计算进来。平方差损失的函数前提是观察结果符合高斯分布，这部分不了解的情况请百度一下，这里进行简单解释，参见下文附录一部分的简介

由上文可知，矩阵内积实际上就是对 $u$ 和 $i$ 的线性运算，针对二分类问题的线性回归，这一假设显然是不成立的。具体可以查看Andrew NG老师的机器学习课程，网上的教程也一大堆，不再赘述，这里只用一张图进行解释。如下图所示，对二分类问题进行线性回归非常不准确。

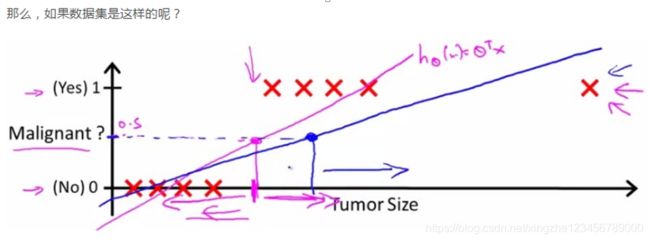
由此，作者将${\hat{u}}_{ui}$限制在 $(0，1)$ 范围内，并将其看成是对应$y_{ui}=1$的概率，因此可以得到下式：
$$p(\mathcal{Y},{\mathcal{Y}}^{-}|P,Q,{\Theta }_f)=\prod _{(u,i)\in \mathcal{Y}}{\hat{y}}_{ui}\prod _{(u,j)\in {\mathcal{Y}}^{-}}(1-{\hat{y}}_{uj})\text{\hspace{1em}(6)}$$

由此，对似然函数取对数后取反，可以得到最小化的目标函数如下：

$$\begin{gathered} L=-\sum _{(u,i)\in \mathcal{Y}}\log {\hat{y}}_{ui}-\sum _{(u,j)\in {\mathcal{Y}}^{-}}\log (1-{\hat{y}}_{uj}) \\ =-\sum _{(u,i)\in \mathcal{Y}\cup {\mathcal{Y}}^{-}}{\hat{y}}_{ui}\log {\hat{y}}_{ui}+(1-{\hat{y}}_{ui})\log (1-{\hat{y}}_{ui}) \end{gathered}$$

上式其实就是对数几率回归，大家一般叫他逻辑回归的东西。

泛化矩阵分解（GMF）

作者用神经网络实现了矩阵分解功能，并在最终的${\hat{y}}_{ui}$的输出上多加了一个sigmoid实现非线性变换。具体变换如下：
$${\varphi }_1(p_u,q_i)=p_u\odot q_i$$
其中，⊙表示矩阵的逐元素相乘。

$${\hat{y}}_{ui}=a_{out}(h^{\mathsf{T}}(p_u\odot q_i))\text{\hspace{1em}(9)}$$
上式9中，$h$表示恒等函数，也就是啥也不干。$a$是激活函数，这里采用了sigmoid函数进行了非线性变换。作者将这一用神经网络泛化后的矩阵分解算法称为泛化矩阵分解（GMF，Generalized Matrix Factorization）模型。

多层感知机（MLP）

这里不进行过多描述，其实就是一个三层的神经网络，每层神经元个数递减，每一层的激活函数援用ReLU函数加快收敛。

GMF和MLP的融合

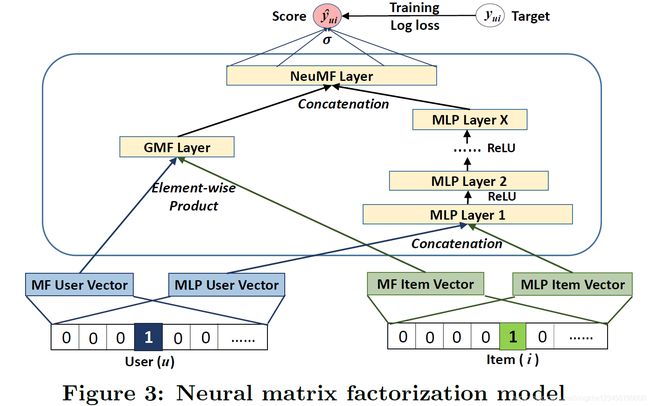
如上图所示，这里对分开的两部分进行融合。如下式所示：
$${\hat{y}}_{ui}=\sigma (h^{\mathsf{T}}a(p_u\odot q_i+W\begin{array}{c}\left[\begin{array}{c}{p}_u\\ q_i\end{array}\right]\end{array}))+b\text{\hspace{1em}(11)}$$
这里表示简单的单层融合，多层同理，不再赘述。

预训练

这里，作者使用Adam分别训练两个自网络，得到比较接近最优解（相较于随机初始化）的局部参数，并直接放到融合后的网络NeuMF的对应部分，剩下的参数使用SGD进行优化。选用SGD的原因是：Adam在保存参数值的同时，还保存了参数的动量（momentum）信息。如果只是使用参数值的话，再去套用Adam进行优化是不合适的。

实验部分、相关工作、总结

这里进行省略，作者提出的NeuMF是使用深度神经网络进行协同过滤算法的比较早的工作。相较于简单的矩阵内积进行互动的估计，使用神经网络很明显加大了模型的表达能力。

附录1： 高斯分布和平方差损失函数

假定y是关于x的线性回归模型：

$$y_i=\theta x_i+{ϵ}_i$$
其中，随机误差${ϵ}_i$独立同分布，且符合高斯分布。可以得出：
$$p({ϵ}_i)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{{ϵ}_i^2}{2{\sigma }^2})$$
则可进一步得出：
$$p(y_i|x_i,\theta )=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{{(y_i-{\theta }_i{x}_i)}^2}{2{\sigma }^2})$$
将i拓展到整个数据集上，则可得到似然函数如下：
$$L(\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{{(y_i-{\theta }_i{x}_i)}^2}{2{\sigma }^2})$$

对数似然函数可以将连乘运算变为求和运算，如下所示：
$$l(\theta )=\log L(\theta )=m\log \frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{2{\sigma }^2}\sum _{i=1}^m(y_i-\theta x_i{)}^2$$
由上式可知，最大化对数似然函数，其实就是最小化平方差损失函数，形式化描述如下：

$$\max l(\theta )<==>\min J(\theta )$$
其中，$J(\theta )$就是平方差损失函数，如下所示：

$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(y_i-\theta x_i{)}^2$$