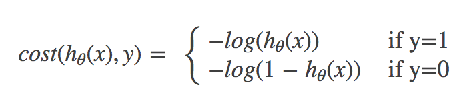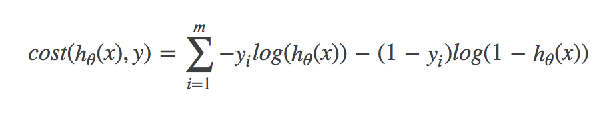ML算法基础——分类算法-逻辑回归
文章目录
- 1.逻辑回归
- 1.1 逻辑回归简介
- 1.2 逻辑回归与线性回归的区别与联系
- 1.3 逻辑回归公式
- 1.4 逻辑回归的损失函数、优化
- 2.逻辑回归案例
- 2.1 sklearn逻辑回归API
- 2.2 良/恶性乳腺癌肿瘤预测案例
- 3.LogisticRegression总结
1.逻辑回归
1.1 逻辑回归简介
逻辑回归(Logistic Regression)是一种用于解决二分类(0 or 1)问题的机器学习方法,用于估计某种事物的可能性。比如某用户购买某商品的可能性,某病人患有某种疾病的可能性,以及某广告被用户点击的可能性等。 注意,这里用的是“可能性”,而非数学上的“概率”,logisitc回归的结果并非数学定义中的概率值,不可以直接当做概率值来用。该结果往往用于和其他特征值加权求和,而非直接相乘。
以胃癌病情分析为例,选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌,值为“是”或“否”,自变量就可以包括很多了,如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的,也可以是分类的。然后通过logistic回归分析,可以得到自变量的权重,从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
1.2 逻辑回归与线性回归的区别与联系
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。 因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
1.3 逻辑回归公式
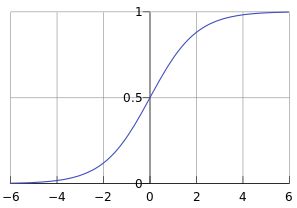
Sigmoid函数
Sigmoid函数,也称为逻辑函数(Logistic function)
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
sigmoid函数是一个s形的曲线,它的取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1。它的这个特性对于解决二分类问题十分重要
逻辑回归公式:
逻辑回归模型所做的假设是
这个函数的意思就是在给定x和 θ \theta θ的条件下 y=1 的概率。
h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_\theta(x)=g(\theta^{T}x)=\frac{1}{1+e^{-\theta^{T}x}} hθ(x)=g(θTx)=1+e−θTx1
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
输出:[0,1]区间的概率值,默认0.5作为阀值
注:g(z)为sigmoid函数
1.4 逻辑回归的损失函数、优化
与线性回归原理相同,但由于是分类问题,
损失函数不一样,只能通过梯度下降求解
cost损失的值越小,那么预测的类别准确度更高
2.逻辑回归案例
2.1 sklearn逻辑回归API
sklearn.linear_model.LogisticRegression
-
sklearn.linear_model.LogisticRegression(penalty=‘l2’, C = 1.0)Logistic回归分类器coef_:回归系数
2.2 良/恶性乳腺癌肿瘤预测案例
原始数据的下载地址:
https://archive.ics.uci.edu/ml/machine-learning-databases/
数据描述
(1)699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤相关的医学特征,最后一列表示肿瘤类型的数值。
(2)包含16个缺失值,用”?”标出。
良/恶性乳腺癌肿分类流程
1、网上获取数据(工具pandas)
2、数据缺失值处理、标准化
3、LogisticRegression估计器流程
from sklearn.datasets import load_boston
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
import pandas as pd
import numpy as np
def logistic():
#构造列标签
column_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size', 'Uniformity of Cell Shape',
'Marginal Adhesion','Single Epithelial Cell Size', 'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses', 'Class']
# 读取数据
data=pd.read_csv('breast-cancer-wisconsin.data',names=column_names)
print(data)
# 缺失值进行处理
data = data.replace(to_replace='?', value=np.nan)
data = data.dropna()
#分割
x_train, x_test, y_train, y_test = train_test_split(data[column_names[1:10]], data[column_names[10]], test_size=0.25)
#标准化处理
std=StandardScaler()
x_train=std.fit_transform(x_train)
x_test=std.transform(x_test)
#逻辑回归预测
lg=LogisticRegression(C=1.0)
lg.fit(x_train,y_train)
y_predict=lg.predict(x_test)
print(lg.coef_)
print("准确率:",lg.score(x_test,y_test))
print("召回率:", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"]))
return None
logistic()
结果:
准确率: 0.9766081871345029
召回率: precision recall f1-score support
良性 0.97 0.99 0.98 111
恶性 0.98 0.95 0.97 60
micro avg 0.98 0.98 0.98 171
macro avg 0.98 0.97 0.97 171
weighted avg 0.98 0.98 0.98 171
3.LogisticRegression总结
应用:广告点击率预测、电商购物搭配推荐
优点:适合需要得到一个分类概率的场景
缺点:当特征空间很大时,逻辑回归的性能不是很好
(看硬件能力)