CV理论基础（三）：基于关键点的特征描述子sift、surf、orb等；LBP、Gabor

基于关键点的特征描述子

SIFT、SURF、ORB

局部特征：SIFT

基于尺度空间不变的特征描述
特点：具有良好的不变性、独特性好信息量丰富、多量性、计算比之前的快

计算步骤：

（1）在DoG尺度空间中获取极值点，即关键点：LoG尺度空间、DoG尺度空间
（2）对关键点处理：位置插值，获得精确的关键点；去除边缘点
（3）关键点的方向估计：找主方向为达到旋转不变性
（4）关键点描述子的生成：区域坐标旋转；计算采样区域的直方图

相关概念

尺度空间

使用不同$\sigma$的LOG对图片进行滤波
使用LOG，则后续计算量极大，可以使用DOG代替LOG，用差分代替微分

高斯金字塔

高斯金字塔是在传统金字塔的基础上，对每层用不同的参数$\sigma$做高斯模糊，是的每一层金字塔有多张高斯模糊图像

octave同一个尺度下参数不同的一组图片，每层从下到上越来越模糊，下面一层的倒数第三张通过隔点降采样得到上面一层最后一张。在小的上面找大特征，大的上面找大特征。

具体过程

（1）计算高斯差分DoG空间
不同octave乘$\sigma$,相同尺度的图片用了不同的高斯核模糊后，相邻相减

在同一组内，不同层图像的尺寸是一样的，后一层图像的高斯平滑因子σ是前一层图像平滑因子的k倍；
在不同组内，后一组第一个图像是前一组倒数第三个图像的二分之一采样，图像大小是前一组的一半；

（2）获取DoG空间极值点
判断极值点：以$X$为检测点，其周围的点，同层的8个点+上层9个点+下层9个点，与监测点相比较都大/都小，则是极值点

DoG空间极值点是关键点
圆半径$\to$特征点尺度；圆心$\to$特征点坐标


（3）特征点方向估计：
在尺度上计算梯度直方图：以特征点为中心，以$3\times 1.5\sigma$归纳到8个方向
获取最高值方向为关键点主方向
为了匹配的稳定性，将超过最高值80%的方向，称为辅方向

为了保证特征矢量具有旋转不变性，需要以特征点为中心，将特征点附近邻域内的图像旋转一个方向角$\theta$，即将原图像x轴转到与主方向相同的方向

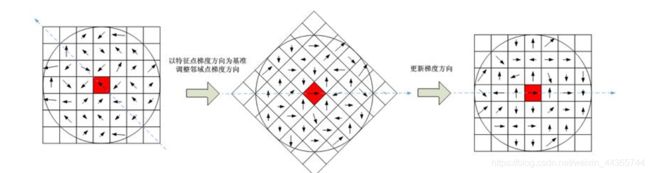
（4）计算特征点描述子
在旋转后的坐标上采样$16\times 16$的像素窗：$4\times 4$网格，8方向直方图，共128维
每一个点对应一个梯度，归纳到8个饼中，串在一起形成一个向量，即关键点基于它主方向的邻近区域的特征描述

缺点

计算太复杂，如果不借助硬件加速或专门的图像处理器很难实现

SURF

SURF（Speeded-Up Robust Features）算子是Herbert Bay等人在2006年提出的，它是对SIFT的改进，可将速度提高3倍。

将SIFT一部分运算进行简化：
（1）将SIFT中的高斯二阶微分的模板Hessian矩阵进行简化，使得卷积平滑操作仅需要转换成加减运算
（2）在方向确定阶段，在圆形区域计算x，y方向的haar小波响应，找到模最大的扇形方向

缺点：尺度不变性，旋转不变性

具体过程

（1）找特征点：对原图进行变换，变换图是原图每个像素的Hessian矩阵行列式的近似值构成的。Hessian求取时先高斯平滑（去噪），再求二阶导数。对于离散的像素点，用模板卷积形成的，使用Haar模板代替即可。
hessain矩阵和高斯平滑结合会形成1，2这样柔和模糊的模板

（2）旋转不变：统计特征点领域内的Haar小波特征。即以特征点为中心，计算半径为6s领域内，统计60度扇形内所有点在水平x和垂直y方向的Haar小波响应总和。然后60度扇形以一定间隔进行旋转，最后将最大值那个扇形方向作为该特征点主方向。

其中，s是特征点所有的尺度值

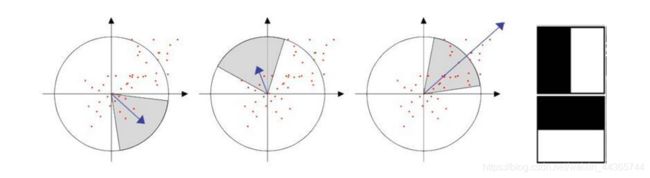
（3）计算：
在特征点周围取一个正方形框，框的边长为20s(s是所检测到该特征点所在的尺度)。该框带方向，即检测出来的主方向。

最终，SURF的特征点特征向量维度是64维。然后把该框分为16个子区域，每个子区域统计25个像素的水平方向和垂直方向的harr小波特征，这里的水平和垂直方向都是相对主方向而言的。

特点

相关概念：Haar-like特征

（1）Haar-like特征分为边缘特征、线性特征、中心特征和对角线特征，这些特征组合成特征模板

特征模板内有白色和黑色两种矩形，并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和

Haar特征值反映了图像的灰度变化情况

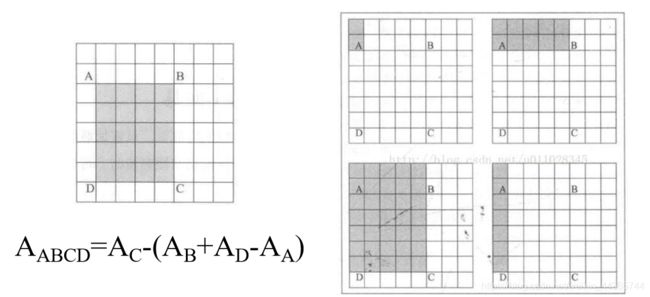
（2）快速计算：积分图

同一个像素如果被包含在不同的Haar-like的特征模板中，会被重复计算多次。积分图是根据四个角点就能计算区域内的像素和的方法。

Hessian矩阵：两阶偏微分矩阵

ORB

ORB特征基于FAST角点的特征点检测和BRIEF特征描述技术，是对FAST角点与BRIEF描述子的一种结合与改进。快，一定程度上比sift准。

FAST角点检测的缺点是：缺乏尺度不变性，可以通过构建高斯金字塔，然后在每一层金字塔图像上检测角点，来实现尺度不变性。
BRIEF缺点：缺乏旋转不变性，需要给BRIEF加上旋转不变性。

ORB对BRIEF的改进：
ORB在计算BRIEF描述子时的坐标系是以关键点为圆心，以关键点和取点区域的形心（圆形）的连线为X轴建立坐标系。
计算形心时，圆心区域上每个点的质量是其对应的像素值。

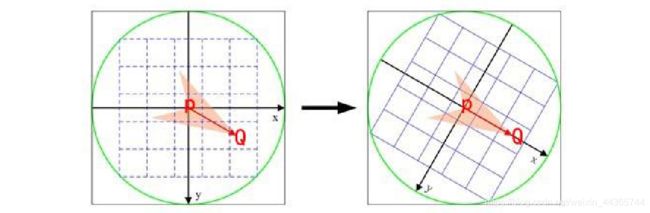
BRIEF

BRIEF需要先平滑图像，然后在特征点周围选择一个Patch，在这个Patch内通过一种选定的方法来挑选出来$n_d$个点对。
比较点对中两点像素的大小，进行如下赋值：

所有$n_d$个点对，都进行比较，生成一个$n_d$长的二进制串。

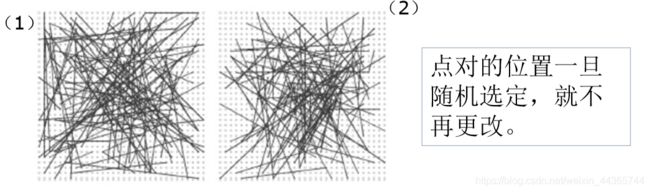
点对生成的方式如下（共5种）：
（1）X和Y都服从在$[-\frac{S}{2},\frac{S}{2}]$范围内的均匀分布，且相互独立
（2）X和Y都服从均值为0，方差为$\frac{S^2}{25}$的高斯分布，且相互独立，即X和Y都以原点为中心，进行同方差的高斯分布。高斯分布中心点密，边缘稀疏

其他特征提取

LBP、Gabor

LBP

LBP 局部二值模式

具体过程：

（1）将每个像素点与周围点大小进行比较：半径为R的圆上，均匀采样P个点，大小量化为0或1。多个bit组成一个数，统计每个数的直方图。

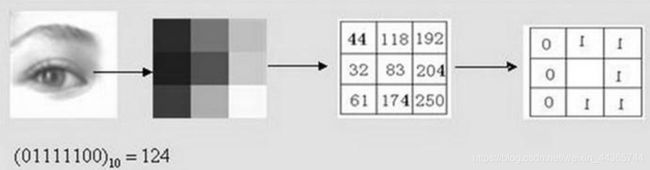
（2）旋转不变性：将LBP周围的二进制码按位旋转，取二进制码最小的值作为最终的LBP值。

改进的LBP：

将$3\times 3$邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，这种LBP特征叫做Extended LBP，也叫Circular LBP

特点

LBP特征具有灰度不变性和旋转不变性

Gabor

Gabor：
Gabor是一个用于边缘提取的线性滤波器，其频率和方向表达与人类视觉系统类似，能够提供良好的方向选择和尺度选择特性，对光照变化不敏感。适合纹理分析。

Gabor滤波器：
使用一个三角函数与一个高斯函数叠加得到Gabor滤波器。Gabor滤波器组类似人类视觉系统，多频率/尺度，多方向。
频域：属于加窗傅里叶变换
空域：一个高斯核函数和正弦平面波的乘积

Gabor滤波器组：
3尺度，8方向

相关资源

LBP特征原理

SIFT检测

SURF检测

Harris角点检测

特征匹配（有bug）