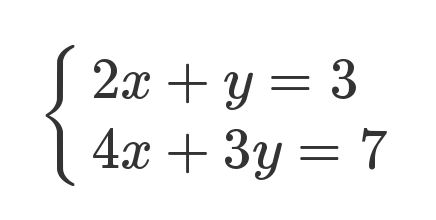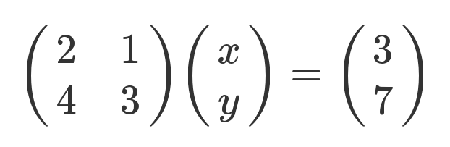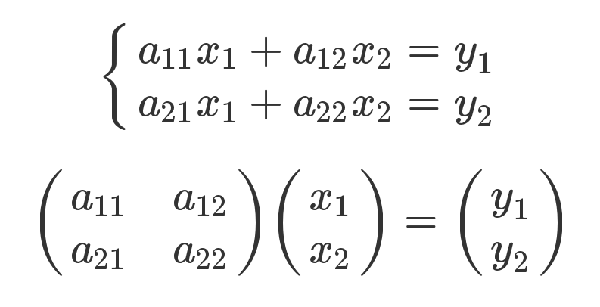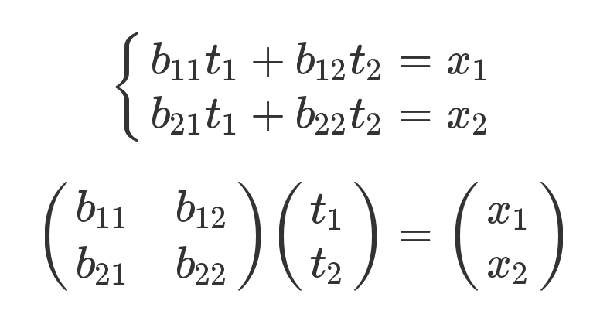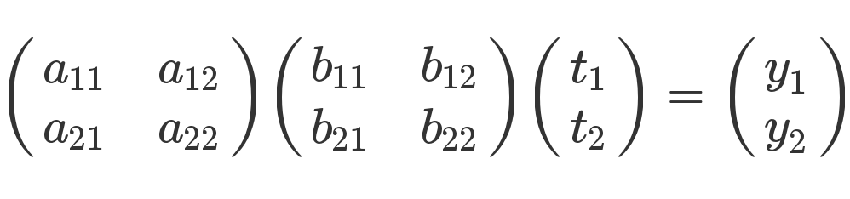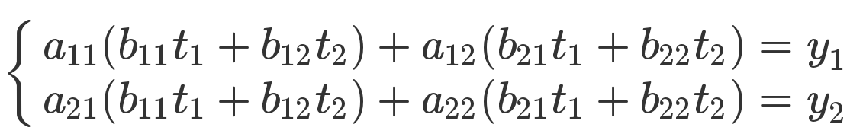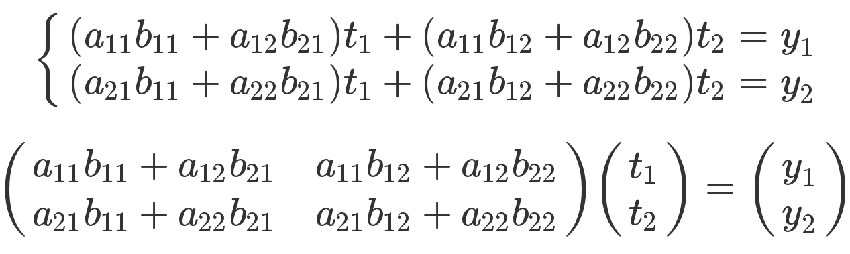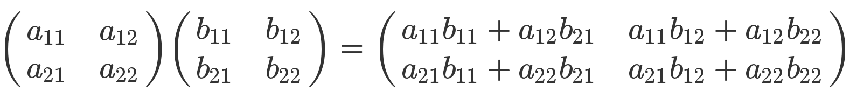矩阵及其基本运算

一、矩阵

矩阵是什么呢？如果你去书本或者网上查资料，会得到如下东西：

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。其定义如下：

由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i , j)元，以数 aij为(i , j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn 。元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

然后还有矩阵的历史、词源来历等等。

但是，看完这些定义等的， 还是糊涂，为什么会有矩阵呢？为什么要这样定义呢？要矩阵有什么用呢？

矩阵是在线性代数这门课里学的，其实，矩阵是应线性方程式而生的，将线性方程组的系数及常数组成矩阵，一开始的矩阵就是这么来的。这样就可以将线性方程式的研究转化为矩阵的研究，简化了研究。线性代数是向量计算的基础，很多重要的数学模型都要用到向量计算，所以，矩阵的研究与计算最终将影响的是向量计算。好了，唠叨了这么多，还没说重点呢：矩阵的本质就是线性方程式，两者是一一对应关系。下面是它的复杂版本矩阵的实质意义：

给定了线性变换，它的系数所构成的矩阵也就确定。线性变换和矩阵之间存在着一一对应的关系。正是由于矩阵和线性变换之间存在着一一对应关系，因此可以利用矩阵来研究线性变换，也可以利用线性变换来解释矩阵的涵义。

二、矩阵的基本运算

矩阵的基本运算为：加、减、乘法及数乘。

加、减法及数乘都很简单，加法就是相同位置的数字加一下，减法也类似。矩阵乘以一个常数，就是所有位置都乘以这个数。

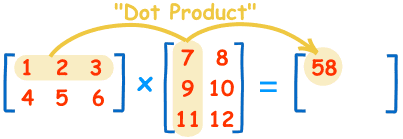
但是乘法就比较复杂了，计算规则是：矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和。

如下图所示,第一个矩阵第一行的每个数字（2和1），各自乘以第二个矩阵第一列对应位置的数字（1和1），然后将乘积相加（ 2 x 1 + 1 x 1），得到结果矩阵左上角的那个值3。

这个规则确实也是有点复杂而奇怪的，上学的时候也仅仅是记住了这个规则，因为要考试嘛，从来没有想过为什么是这样，今天查矩阵的时候偶然看到一位前辈的文章：http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html，认真拜读后整理过来，加深一下自己对矩阵乘法规则的理解和矩阵本质的理解。

结合矩阵的本质，从线性方程式的角度，理解矩阵乘法就毫无难度。

下面是一组线性方程式。

矩阵的最初目的，只是为线性方程组提供一个简写形式。

老实说，从上面这种写法，已经能看出矩阵乘法的规则了：系数矩阵第一行的2和1，各自与 x 和 y 的乘积之和，等于3。不过，这不算严格的证明，只是线性方程式转为矩阵的书写规则。

下面是严格的证明。有三组未知数 x、y 和 t，其中 x 和 y 的关系如下。

x 和 t 的关系如下。

有了这两组方程式，就可以求 y 和 t 的关系。从矩阵来看，很显然，只要把第二个矩阵代入第一个矩阵即可。

从方程式来看，也可以把第二个方程组代入第一个方程组。

上面的方程组可以整理成下面的形式。

最后那个矩阵等式，与前面的矩阵等式一对照，就会得到下面的关系。

矩阵乘法的计算规则，从而得到证明。

---

参考：

1. http://baike.baidu.com/link?url=3BjWZ7twHOZmVKprbSeO8xAd0-_OUKRzXy6FrwzDpwtDCO8Jd3dB_px78mj-XkiqWrTcegQy0ZWivgQvWboZQI1z5WXXIWnjaVB7i3Q1KFq#5
2. http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html
3. http://wenku.baidu.com/link?url=N-GcV95HP8MOgTBSTLwG9TaEATo3ktkmmD1aCBVmngJuXc5_gvWIuLzeLieY5NGHYeTSGyaDRwnExXmyl4FGjm1iU4u-ZucLdxplWmsxLRK