【算法】BFS广度优先搜索算法解决迷宫问题以及岛屿数量问题
一.BFS
1.介绍
BFS(Breath First Search)广度优先搜索法,可以断句为“广度优先”搜索法,顾名思义,该算法的优势在于“广度优先”,与之后“深度优先”的搜索法不同,“广度优先”搜索会将所有数据遍历,以找到起点到终点之间的最短路径。算法通常应用在找最短路径以及遍历中,但是不能将通往终点所走过的路径保存列出,例如在走迷宫问题中,广度优先搜索只能找到起点到终点的最短路径,而不能标记出起点到终点的路径应该怎么走,想要解决这一问题需要借助深度优先算法。此外,广度优先算法需要借助数据结构“队列”来完成,而深度优先算法则需要借助“栈”来完成。
关于下文所用到的“队列”代码,可以参考本人之前写过的一篇文章:【数据结构】圆形结构——循环队列 ,下文所用到的所有关于队列的方法均是此文章所处,所以就不一 一 列举了。
2.图解
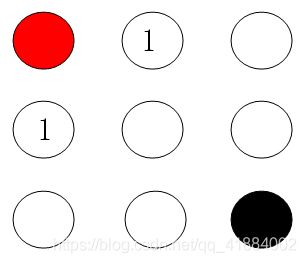
假如有以下地标:
问:如果只能向上下左右四个方向运动,从红色到黑色需要多少步数?广度优先搜索的做法是以红色点开始,寻找相邻节点,记录当前步数,判断是否为目标节点,若不是则继续寻找相邻节点,直到找到目标节点为止。
相邻节点均不是目标节点,继续往下走:
相邻节点均不是目标节点,继续往下走:
相邻节点是目标节点,最短步伐数为3.
二.迷宫最短步数
1.问题描述
BFS最经典的问题之一,寻找迷宫中起点到终点的最短路径:{{0, 0, 1, 0, 1},
{0, 1, 1, 1, 0},
{0, 0, 0, 0, 0},
{0, 1, 1, 1, 0},
{0, 0, 0, 1, 0}};
2.解题思路
题目可以使用广度搜索的方法进行解答,具体可以接替思路如下:
1.记录二维网格坐标位置、是否为墙壁、是否走过等状态
2.将起始节点压入队列中,寻找队列中第一个节点的相邻节点
3.遍历相邻节点,先判断该节点是否为目标节点,是则返回步数,不是则判断该节点是否走过或者为墙壁,如果“走过”或者“是墙壁”,则不进行任何操作继续遍历下一个节点,如果不是“走过”或者“是墙壁”,则将节点压入队列中。
4.遍历完一边相邻节点后,将队列的所有节点中的步数全部设置为第N步
5.压入队列中第一个节点,继续从第二点重复,知道队列为空
6.输出目标节点所记录的步数,即为最短步数
3.代码解析
1.对于解题思路第一点:二维网格进行状态添加,本人使用结构体+vector的方式,方便再遍历时进行操作:
struct Node
{
int _x; //节点坐标x
int _y; //节点坐标y
int _value; //节点的值
int _Step; //记录步数
bool _IsWall; //是否为岛屿
bool _IsWalked; //该点是否已经被走过
};
std::vector> push_Node(std::vector> push_into)
{
std::vector> push;
int state;
for (int i = 0; i < push_into.size(); i++)
{
std::vector into;
for (int j = 0; j < push_into[i].size(); j++)
{
if (push_into[i][j] == 1)
state = true;
else
state = false;
Node node{i,j,push_into[i][j],0,state,false};
into.push_back(node);
}
push.push_back(into);
}
return push;
}
2.寻找指定节点的相邻节点,详细代码可参考我之前写过的文章:【C/C++】获取二维数组相邻八个/四个方向的数据
std::vector Find_Beighbors(int x,int y,std::vector> vec)
{
int max_x = (vec.size() - 1);
int max_y = ((vec[x].size()) - 1);
std::vector list; //扩列存储相邻元素
for (int dx = (x > 0 ? -1 : 0); dx <= (x < max_x ? 1 : 0); ++dx)
{
for (int dy = (y > 0 ? -1 : 0); dy <= (y < max_y ? 1 : 0); ++dy)
{
if ((dx == 0 || dy == 0) && (dx+dy != 0))
{
list.push_back(vec[x + dx][y + dy]);
}
}
}
return list;
} 3.使用BFS方法,实现解题思路的第二三四五点:
std::vector> BFS(Node root ,Node target)
{
CircularQueue queue(10);
std::vector neighbors;
std::vector> Node_Array = push_Node(test);
//init
queue.enQueue(root);
(Node_Array[root._x][root._y])._IsWalked = true; //标记是否走过
while (!queue.isEmpty())
{
neighbors = Find_Beighbors(queue.Get_value()._x, queue.Get_value()._y, Node_Array); //寻找相邻数据
for (int i = 0; i < neighbors.size(); i++) //将相邻数据压入队列
{
if (!neighbors[i]._IsWall)
{
if (!neighbors[i]._IsWalked)
{
queue.enQueue(neighbors[i]);
((Node_Array[neighbors[i]._x][neighbors[i]._y])._Step) = ((Node_Array[queue.Get_value()._x][queue.Get_value()._y])._Step) + 1;//记录步数
((Node_Array[neighbors[i]._x][neighbors[i]._y])._IsWalked) = true; //标记是否走过
}
else
{
continue;
}
}
if (queue.Get_value()._x == target._x && queue.Get_value()._y == target._y)
return Node_Array;
}
queue.deQueue(); //将第一个数据抛出
}
} 4.实际使用情况
No.1 二维网格
{{0, 0, 1, 0, 1},
{0, 1, 1, 1, 0},
{0, 0, 0, 0, 0},
{0, 1, 1, 1, 0},
{0, 0, 0, 1, 0}};
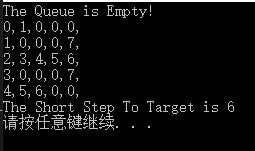
起始节点坐标:(0,0),目标节点坐标:(4,4),输出为:
起始节点坐标:(0,0),目标节点坐标:(4,2),输出为:
三.岛屿数量
1.问题描述
力扣中有一道这样的题目:给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿 总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。此外,你可以假设该网格的四条边均被水 包围。
示例 1:
输入:
[
['1','1','1','1','0'],
['1','1','0','1','0'],
['1','1','0','0','0'],
['0','0','0','0','0']
]
输出: 1
示例 2:
输入:
[
['1','1','0','0','0'],
['1','1','0','0','0'],
['0','0','1','0','0'],
['0','0','0','1','1']
]
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
2.解题思路
题目可以使用广度搜索的方法进行解答,具体可以接替思路如下:
1.记录二维网格坐标位置、是否为岛屿、是否走过等状态
2.遍历二维网格,如果节点满足条件(是岛屿并且没有走过),则将该节点压入队列
3.寻找队列中第一个数据的相邻节点,重复第二点,一直到队列为空
4.当队列为空时,代表已经遍历了一个岛屿,所以要记录岛屿数
5.继续重复第二点,知道所有的二维网格全部被遍历完成,所记录岛屿数即为答案
3.代码解析
1.对于解题思路第一点:二维网格进行状态添加,本人使用结构体+vector的方式,方便再遍历时进行操作:
typedef struct Node
{
int _x; //节点坐标x
int _y; //节点坐标y
char _value; //节点的值
bool _IsWall; //是否为岛屿
bool _IsWalked; //该点是否已经被走过
};
std::vector> push_Node(std::vector> push_into)
{
std::vector> push;
int state;
for (int i = 0; i < push_into.size(); i++)
{
std::vector into;
for (int j = 0; j < push_into[i].size(); j++)
{
if (push_into[i][j] == '1')
state = true;
else
state = false;
Node node{ i,j,push_into[i][j],state,false };
into.push_back(node);
}
push.push_back(into);
}
return push;
} 2.寻找指定节点的相邻节点,详细代码可参考我之前写过的文章:【C/C++】获取二维数组相邻八个/四个方向的数据
std::vector Find_Beighbors(int x, int y, std::vector> vec)
{
int max_x = (vec.size() - 1);
int max_y = ((vec[x].size()) -1 );
std::vector list; //扩列存储相邻元素
for (int dx = (x > 0 ? -1 : 0); dx <= (x < max_x ? 1 : 0); ++dx)
{
for (int dy = (y > 0 ? -1 : 0); dy <= (y < max_y ? 1 : 0); ++dy)
{
if ((dx == 0 || dy == 0) && (dx + dy != 0))
{
list.push_back(vec[x + dx][y + dy]);
}
}
}
return list;
} 3.开启BFS搜索,从坐标(0,0)开始一直到最后,具体代码步骤在前面解题思路(第三第四点)已经说明,不再累赘:
int BFS(Node node, std::vector>& push)
{
CircularQueue queue(10);
queue.enQueue(node);
push[queue.Get_value()._x][queue.Get_value()._y]._IsWalked = true;
while (!queue.isEmpty())
{
std::vector neighbors = Find_Beighbors(queue.Get_value()._x, queue.Get_value()._y, push); //寻找相邻数据
for (int i = 0; i < neighbors.size(); i++)
{
if (neighbors[i]._IsWall)
{
if (!neighbors[i]._IsWalked)
{
queue.enQueue(neighbors[i]); //压入队列
((push[neighbors[i]._x][neighbors[i]._y])._IsWalked) = true; //标记是否走过
}
}
}
queue.deQueue(); //将第一个数据抛出
}
return true;
} 4.在使用BFS方法前需进行二维网格遍历以及记录岛屿数量(第二第五点),代码如下:
int numIslands(std::vector>& grid)
{
std::vector> Vec = push_Node(grid);
int NumLands = 0;
for (int i = 0; i < Vec.size(); i++)
{
for (int j = 0; j < Vec[i].size(); j++)
{
if (Vec[i][j]._IsWall)
{
if (!Vec[i][j]._IsWalked)
{
NumLands += BFS(Vec[i][j],Vec);
}
}
}
}
return NumLands;
} 4. 实际使用情况
No.1 二维网格
{ { '1','1','0','1','0' },
{ '1','1','0','1','0' },
{ '1','1','0','0','1' },
{ '0','1','1','0','0' } };
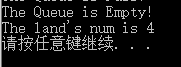
输出为:
No.2 二维网格
{ { '1','1','0','1','0' },
{ '0','1','0','1','0' },
{ '1','1','0','0','1' },
{ '0','0','1','0','0' } };
输出为: