leetcode.DFS or BFS专题

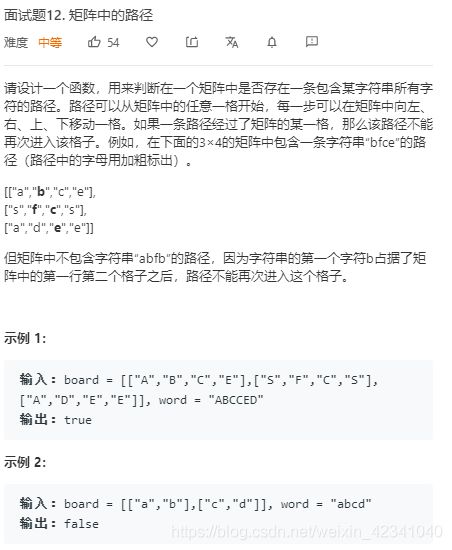
矩阵中的路径

class Solution {
public:
	int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };
	bool exist(vector<vector<char>>& board, string word) {
		int r = board.size();
		int c = board[0].size();
		vector<vector<bool>> seen(r, vector<bool>(c, false));
		vector<pair<int, int>>v;//存放所有word[0]的坐标
		for (int i = 0; i < r; ++i) {
			for (int j = 0; j < c; ++j) {
				if (word[0] == board[i][j]) {
					v.push_back(make_pair(i, j));
				}
			}
		}
		for (int i = 0; i < v.size(); ++i) {
			if (dfs(v[i], seen, 1, word, board))
				return true;
		}
		return false;
	}
	bool dfs(pair<int, int>v, vector<vector<bool>>& seen, int index, string& word, vector<vector<char>>& board) {
		if (index == word.size())
			return true;
		int cdx, cdy;
		int x = v.first;
		int y = v.second;
		seen[x][y] = true;
		for (int i = 0; i < 4; ++i) {
			cdx = x + dx[i];
			cdy = y + dy[i];
			if (cdx >= 0 && cdx < seen.size() && cdy >= 0 && cdy < seen[0].size() && !seen[cdx][cdy]) {
				if (word[index] == board[cdx][cdy] && dfs(make_pair(cdx, cdy), seen, index + 1, word, board)) {
					return true;
				}
			}
		}
		seen[x][y] = false;//回溯
		return false;

	}
};

139.单词拆分

思路：DFS

超时

class Solution {
public:
	bool wordBreak(string s, vector<string>& wordDict) {
		// unordered_setset;
		// for(auto v:wordDict)
		//     set.insert(v);
		vector<string>v;
		for (auto item : wordDict)
			v.push_back(item);
		int n = v.size();
		int m = s.size();
		if (dfs(s, 0, m, n, v))return 1;
		return 0;
	}
	bool dfs(string& s, int ind, int m, int n, vector<string>& v) {
		if (ind == m /*&& s==t*/)return true;
		if (ind > m )return false;
		for (int i = 0; i < n; i++) {
			int b = v[i].size();
			if (ind + b <= m && s.substr(ind, b) == v[i] && dfs(s, ind + b, m, n, v)) {
				return true;
			}
		}
		return false;
	}
};

优化，加个记忆数组vis，记录该点能否继续走

class Solution {
public:
	bool wordBreak(string s, vector<string>& wordDict) {
		vector<string>v;
		for (auto item : wordDict)
			v.push_back(item);
		int n = v.size();
		int m = s.size();
		vector<bool>vis(m,true);	# !!!!!!!
		if (dfs(s, 0, m, n, v, vis))return 1;
		return 0;
	}
	bool dfs(string& s, int ind, int m, int n, vector<string>& v, vector<bool>&vis) {
		if (ind == m)return true;
		if (ind > m || !vis[ind])return false;
		for (int i = 0; i < n; i++) {
			int b = v[i].size();
			if (ind + b <= m && s.substr(ind, b) == v[i] && dfs(s, ind + b, m, n, v,vis)) {
				return true;
			}
		}
		vis[ind] = false;//这个点已经进行不下去了（没有任何可以匹配的）
		return false;
	}
};

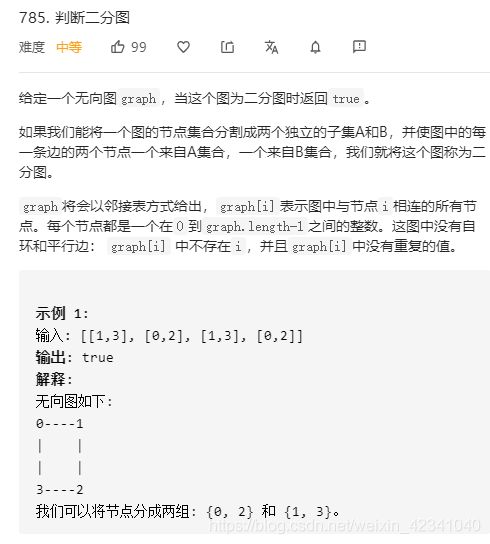
785. 判断二分图

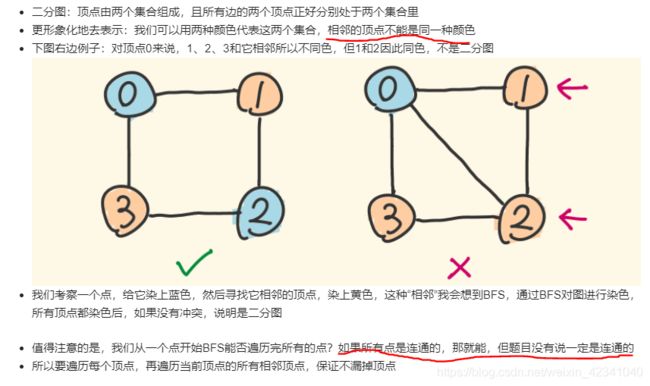
思路 BFS

class Solution {
public:
	bool isBipartite(vector<vector<int>>& graph) {
		int n = graph.size();
		vector<int>seen(n, 0);//未染色0,颜色A：1,颜色B：2
		for (int j = 0; j < n; j++) {//可能出现不连通的图（几个节点是独立的）
			if (seen[j] != 0)//已经染色，跳过
				continue;
			queue<int>q;
			q.push(j);
			seen[j] = 1;//假设染色1
			while (!q.empty()) {
				int top = q.front();
				q.pop();
				int color = seen[top];
				int sun_col = color == 1 ? 2 : 1;
				for (int i = 0; i < graph[top].size(); i++) {
					if (seen[graph[top][i]] == 0) {
						q.push(graph[top][i]);
						seen[graph[top][i]] = sun_col;

					}
					else {
						if (seen[graph[top][i]] != sun_col)
							return false;
					}

				}
			}

		}
		return true;
	}
};

复杂度

1514.概率最大的路径

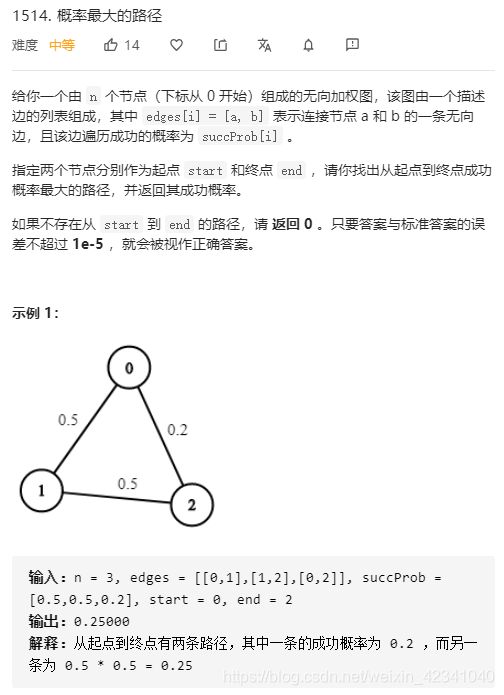
思路：dfs超时，用bfs + dijkstra

class Solution {
public:
	double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
		vector<bool> vi(n, false);//访问数组

		vector<vector<pair<double, int>>> path(n, vector<pair<double, int>>());
		for (int i = 0; i < edges.size(); i++) {//邻接表
			auto& e = edges[i];
			path[e[0]].push_back({ succProb[i], e[1] });
			path[e[1]].push_back({ succProb[i], e[0] });
		}

		priority_queue<pair<double, int>> pq;//默认最大堆，根据pair中首个元素double排序
		pq.push({ 1.0, start });		//首元素，概率设置为1

		while (!pq.empty()) {
			auto [curProb, cur] = pq.top();//这种写法仅支持c++17之后
			pq.pop();

			if (vi[cur]) continue;
			vi[cur] = true;

			if (cur == end) return curProb;

			for (auto[nextProb, next] : path[cur]) {//对相邻节点 bfs
				if (vi[next]) continue;
				pq.push({ curProb * nextProb, next });
			}
		}

		return 0;
	}

};

第一次cur == end就返回了，为什么就是对的呢

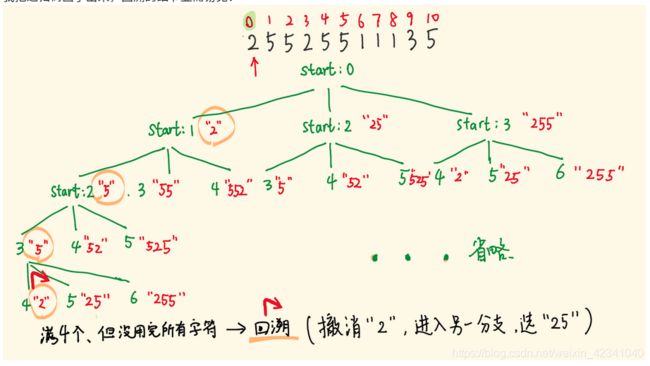
93.复原IP地址

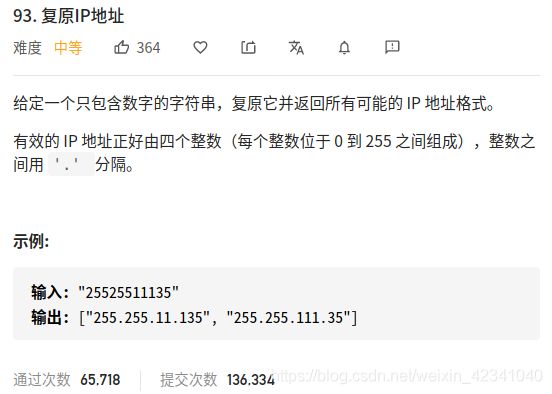
DFS和回溯

class Solution {
    vector<string>res;

public:
    vector<string> restoreIpAddresses(string s) {
        string temp = "";
        dfs(s, 0, temp, 0);
        return res;
        
    }
    void dfs(string& s,int ind,string& temp,int cnt) {
        if(ind == s.size() && cnt == 4) {
            int sz = temp.size();
            res.push_back(temp.substr(0, sz - 1));
            return;
        }
        //以及达到4组且还没组成
        if(cnt == 4)
            return;   
        for(int i = 1;i <= 3;i++) {
            //边界条件！
            if(ind + i > s.size()) continue;
            string t = s.substr(ind, i);
            //不能有前导0
            if(i != 1 && t[0] == '0')
                continue;
            //3位时不能大于255
            else if(i == 3 && atoi(t.c_str()) > 255)
                continue;
            temp += t;
            temp += '.';
            dfs(s, ind + i, temp, cnt + 1);
            //回溯
            for(int j = 0; j < i + 1; j++)
                temp.pop_back();
        }

    }
};