【论文笔记】AVSM：结合了仿射配准和vSVF配准的医学图像配准模型

本文是论文《Networks for Joint Affine and Non-parametric Image Registration》的阅读笔记。

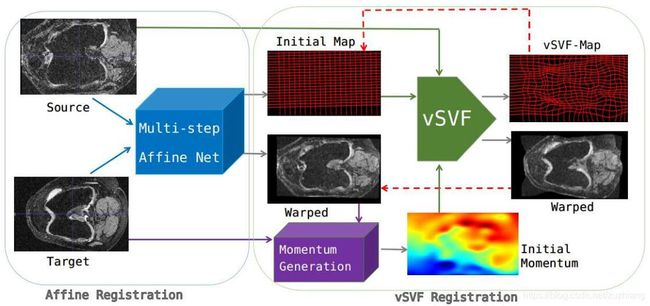
文章提出了一个名为AVSM（Affine-vSVF-Mapping）的端到端3D医学图像配准模型，该模型结合了仿射配准和矢量动量参数化静态速度场模型（ a vector momentum-parameterized stationary velocity field（vSVF） model）。模型有三个阶段（stage），在第一阶段，通过多步的仿射网络来预测一个仿射变换参数；在第二阶段，使用类UNet网络生成一个动量，从而可以通过平滑计算出一个速度场；在第三阶段，使用一个独立的基于图的vSVF组件来基于当前转换映射做无参的微调。

一、相关工作

当图像具有相似的灰度值分布时，通常采用MSE来评估灰度值的相似性；而在多模配准中，NCC和MI指标会更合适。

微分同胚转换可以通过优化足够平滑的速度场来实现，此时，空间转换可以通过积分来恢复（通过积分得到逆转换）。这样的方法包括LDDMM和Diffeomorphic Demons等。

由于空间转换网络（STN）在配准模型中的使用，实现了模型的端到端的训练。

现有的基于深度学习的配准模型存在诸多局限：

• 这些方法通常会假定图像已经实现预配准过，即进行过刚性或仿射配准。这种预对齐可以通过特定的网络或标准数值优化的方式来进行，在前一种方法中，配准方法不再是端到端的，在后一种方法中，预配准成为了计算的瓶颈；
• 很多方法受限于内存/显存的大小，通常可以通过改为对2D图像会对3D patch进行配准以减少资源开销；
• 这些方法没有进行迭代的改进（refinement）。

本文的贡献有：

• 提出了一个新颖的矢量动量参数化的静态速度场配准模型，矢量动量长允许将平滑和转换参数的预测解构，因此可以得到足够平滑的速度场以及适用于大位移的微分同胚；
• 模型是端到端的，并且结合了仿射配准和vSVF配准；
• 在仿射配准和vSVF配准组件中都采用了多步配准的方法，从而改善了配准的效果；
• 结果只经过一次配准映射得到，避免了多次插值而带来的误差；
• 在仿射配准和vSVF配准组件中都采用了逆一致性损失，从而让模型忽略输入图像的顺序，即从A配准到B和从B配准到A的结果相似。

AVSM的网络架构如上图所示，在仿射配准阶段，采用多步的仿射网络来预测仿射变换参数；在vSVF配准阶段，使用类UNet网络产生一个动量，并由此计算一个速度场，然后初始映射和动量被喂到vSVF组件中来产生最终的转换映射。在以上过程中源图像只做一次插值，由此也避免了图像模糊。

在处理3D图像时，如果图像的大小只有原图的一半，则需要的计算和内存/显存只有原来的$\frac{1}{8}$。

二、方法

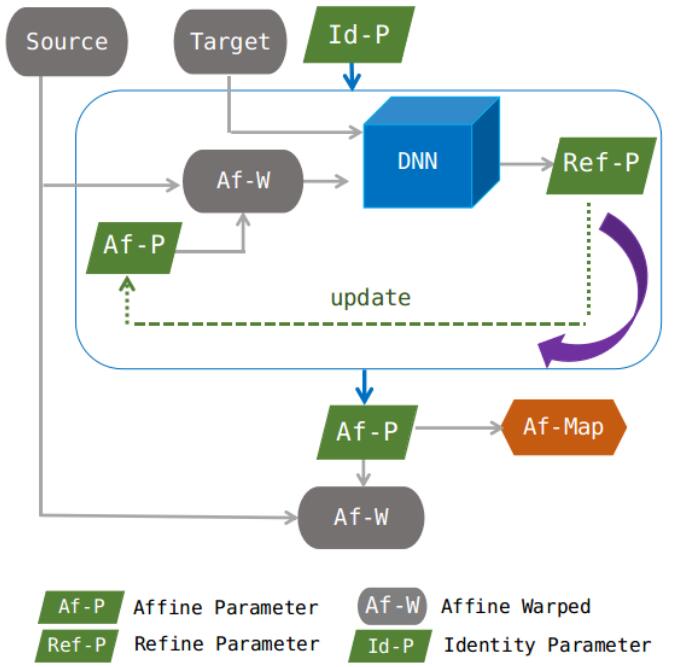
1. 多步仿射网络

现有的大多数无参数配准方法由于有正则项惩罚，所以对仿射变换不是不变的，因此在无参配准之前通常会先进行预配准，即仿射配准，以考虑全局的大位移和旋转。

模型应该足够灵活以同时适应小的和大的仿射变形。所以采用多步的方法得到最终的仿射变换，这种策略显著的提高了模型精度和稳定性。

上图是多步仿射配准的网络结构。多步仿射配准网络是一个多次出现的网络，以逐渐的改进仿射变换。为了避免多次三线性插值带来的数值不稳定性和数值消散，文章采用的是直接更新仿射参数而不是在中间步骤对图像进行重采样。用$\Gamma =(Ab)$来表示仿射参数，其中$A\in {\mathbb{R}}^{d\times d}$表示线性转换矩阵，$b\in {\mathbb{R}}^d$表示位移，$d$是图像的维度。仿射参数更新的规则如下：
$$\begin{array}{l}{A}_{(t)}={\tilde{A}}_{(t)}{A}_{(t-1)},b_{(t)}={\tilde{A}}_{(t)}{b}_{(t-1)}+{\tilde{b}}_{(t)}\\ \text{s.t.}{A}_{(0)}=I,b_{(0)}=0\end{array}$$
其中，${\tilde{A}}_{(t)}，A_{(t)}$表示第$t$步的线性变换矩阵输出和合成结果。相似的，$ \tilde b_{(t)}，b_{(t)}$表示第$t$步的仿射变换参数输出和合成结果。仿射映射可以通过下式得到：$\Phi_{a}^{-1}(x, \Gamma)=A_{\left(t_{\text {last}}\right)} x+b_{\left(t_{\text {last}}\right)}$。

2. 多步仿射网络的损失

损失包括三部分：图像相似性损失$L_{a-sim}$，正则项$L_{a-reg}$和鼓励变换对称的损失$L_{a-sym}$。让$I_0$和$I_1$分别表示源图像和目标图像，上标${}^{st}$和${}^{ts}$分别表示从$I_0$到$I_1$的配准和从$I_1$到$I_0$的配准。

1）图像相似性损失$L_{a-sim}\left(I_0,I_1,{\Phi }_a^{-1}\right)$

可以是NCC、LNCC（localized NCC）、MSE等。本文使用的是mk-LNCC（multi-kernel LNCC）。让$V$ 表示图像的体积，$x_i,y_i$表示配准后的源图像和目标图像中的第$i$个体素，$N_s$表示大小为$s\times s\times s$的滑动窗口的个数，${\zeta }_j^s$表示中心点在第$j$个体素的窗口，$\overline{x_j},\overline{y_j}$表示配准后源图像和目标图像在窗口${\zeta }_j^8$内的灰度值的平均值。窗口大小为$s$的LNCC记为$k_s$，其定义如下：
$${\kappa }_s(x,y)=\frac{1}{N_s}\sum _j\frac{{\sum }_{i\in {\zeta }_j^s}\left(x_i-{\bar{x}}_j\right)\left(y_i-{\bar{y}}_j\right)}{\sqrt{{\sum }_{i\in {\zeta }_j^s}{\left(x_i-{\bar{x}}_j\right)}^2{\sum }_{i\in {\zeta }_j^s}{\left(y_i-{\bar{y}}_j\right)}^2}}$$
定义mk-LNCC为具有不同窗口大小的LNCC的加权和。

图像相似性损失为：
$$\begin{array}{l}{L}_{a-sim}\left(I_0,I_1,\Gamma \right)={\sum }_i{\omega }_i{\kappa }_{s_i}\left(I_0\circ {\Phi }_a^{-1},I_1\right)\\ \text{ s.t. }{\Phi }_a^{-1}(x,\Gamma )=Ax+b\text{ and }{\sum }_i{\omega }_i=1,w_i\ge 0\end{array}$$

2）正则项损失$L_{a-reg}(\Gamma )$

惩罚合成仿射变换与恒等变换的偏差：
$$L_{a-reg}(\Gamma )={\lambda }_{ar}\left(\Vert A-I{\Vert }_F^2+\Vert b{\Vert }_2^2\right)$$
其中$\Vert \cdot {\Vert }_F$表示Frobenius正则，${\lambda }_{ar}\ge 0$是依赖于epoch的权重系数，在训练开始时较大，以限制大的形变，然后逐渐衰减到0。

3）对称损失$L_{a-sym}(\Gamma ,{\Gamma }^{ts})$

鼓励配准的逆一致性，即鼓励从源图像到目标图像的变换是从目标图像到源图像变换的逆变换，用公式表示为：$A^{ts}(Ax+b)+b^{ts}=x):L_{a-sym}\left(\Gamma ,{\Gamma }^{ts}\right)={\lambda }_{as}\left({\Vert A^{ts}A-I\Vert }_F^2+{\Vert A^{ts}b+b^{ts}\Vert }_2^2\right)$，其中${\lambda }_{as}\ge 0$。

总损失为：
$$\begin{array}{rl}{\mathcal{L}}_a\left(I_0,I_1,\Gamma ,{\Gamma }^{ts}\right)=& {\ell }_a\left(I_0,I_1,\Gamma \right)+{\ell }_a\left(I_1,I_0,{\Gamma }^{ts}\right)\\ & +L_{a-sym}\left(\Gamma ,{\Gamma }^{ts}\right)\end{array}$$
其中${\ell }_a\left(I_0,I_1,\Gamma \right)=L_{a-sim}\left(I_0,I_1,\Gamma \right)+L_{a-reg}(\Gamma )$。

3. 矢量动量参数化SVF

1）vSVF方法

为了捕获大的变形并保证微分同胚变换，通常使用流体机制的配准算法。此时，转换映射${\varphi }^3$可以通过速度场$v(x,t)$对时间积分来得到。控制微分方程为：${\Phi }_t(x,t)=v(\Phi (x,t),t),\Phi (x,0)={\Phi }_{(0)}(x)$，其中${\Phi }_{(0)}$是初始映射。对于足够平滑的速度场来说，可以获得一个微分同胚变换，通过对不平衡进行惩罚而保证速度场的平滑性，即：
$$\begin{array}{l}{v}^{\ast }=\underset{v}{\mathrm{argmin}}{\lambda }_{vr}{\int }_0^1\Vert v{\Vert }_L^2\mathrm{d}t+\mathrm{sim}\left[I_0\circ {\Phi }^{-1}(1),I_1\right]\\ \text{ s.t. }{\Phi }_t^{-1}+D{\Phi }^{-1}v=0\text{ and }{\Phi }^{-1}(0)={\Phi }_{(0)}^{-1}\end{array}$$
其中$D$表示雅克比行列式，$\Vert v{\Vert }_L^2=⟨L^{†}Lv,v⟩$是通过微分操作$L$和其共轭$L^{†}$所定义的空间正则。由于动量$m=L^{†}Lv$，正则又可以表示为：$\Vert v{\Vert }_L^2=⟨m,v⟩$。SVF配准算法是直接优化速度场$v$，而本文提出一个矢量动量SVF（vSVF）方程，其表达式如下：
$$\begin{array}{l}{m}^{\ast }=\underset{m_0}{\mathrm{argmin}}{\lambda }_{vr}⟨m_0,v_0⟩+\mathrm{Sim}\left[I_0\circ {\Phi }^{-1}(1),I_1\right],\text{ s.t. }\\ {\Phi }_t^{-1}+D{\Phi }^{-1}v=0,{\Phi }^{-1}(0)={\Phi }_{(\cap )}^{-1},v_0={\left(L^{†}L\right)}^{-1}{m}_0\end{array}$$
其中，$m_0$表示矢量动量，${\lambda }_{vr}>0$是常数，该方程可以看作是简化的矢量动量参数化的LDDMM方程。该方程的有点事它允许我们通过深度网络来预测动量而显式的控制空间平滑，进而产生平滑的速度场，而不是直接预测速平滑的度场。

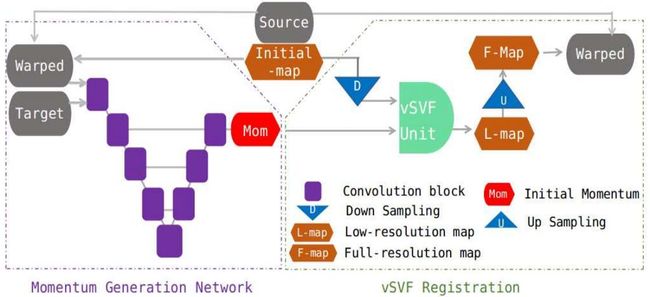
2）vSVF配准网络

上图是vSVF配准网络框架，分为两部分：一是动量生成网络，以配准后的源图像和目标图像作为输入，输出低分辨率的动量；二是vSVF配准部分。预测的动量和下采样的初始化映射被输入到vSVF单元，然后输出最后经过上采样得到全分辨率的转换映射。在vSVF单元中，通过对动量进行平滑而得到速度场，然后用它来解对流方程${\Phi }_{(\tau )t}^{-1}+D{\Phi }_{(\tau )}^{-1}v=0$，然后得到最终的变换映射。初始映射可以是仿射映射，也可以是通过之前的vSVF步骤得到的映射。

动量生成网络

使用四阶Runge-Kutta方法来对时间积分并将所有具有中心差分的空间导数离散化。因此，减少了内存的需要，网络输出的是低分辨率的动量。在实操时，移除了UNet中解码器的最后一层，以产生低分辨率的动量。

vSVF的损失

损失也分为三部分，相似性损失和仿射网络中的相同，正则项损失用来乘法速度场，即：
$$L_{v-reg}\left(m_0\right)={\lambda }_{vr}\Vert v{\Vert }_L^2={\lambda }_{vr}⟨m_0,v_0⟩$$
其中，$v_0=(L^{†}L{)}^{-1}{m}_0$，把$(L^{†}L{)}^{-1}$看作是具有多高斯核的卷积。

对称性损失
$$L_{v-sym}\left({\Phi }^{-1},{\left({\Phi }^{ts}\right)}^{-1}\right)={\lambda }_{vs}{\Vert {\Phi }^{-1}\circ {\left({\Phi }^{ts}\right)}^{-1}-id\Vert }_2^2$$
其中$id$表示恒等映射，${\lambda }_{vs}\ge 0$表示对称权重，$({\Phi }^{ts}{)}^{-1}$表示从目标图像到源图像的配准映射，${\Phi }^{-1}$表示从源图像到目标图像的配准映射。

总损失：
$$\begin{array}{r}{\mathcal{L}}_v\left(I_0,I_1,{\Phi }^{-1},{\left({\Phi }^{ts}\right)}^{-1},m_0,m_0^{ts}\right)={\ell }_v\left(I_0,I_1,{\Phi }^{-1},m_0\right)\\ +{\ell }_v\left(I_1,I_0,{\left({\Phi }^{ts}\right)}^{-1},m_0^{ts}\right)\\ +L_{v-sym}\left({\Phi }^{-1},{\left({\Phi }^{ts}\right)}^{-1}\right)\end{array}$$
其中，${\ell }_v\left(I_0,I_1,{\Phi }^{-1},m_0\right)=L_{v-\mathrm{sim}}\left(I_0,I_1,{\Phi }^{-1}\right)+L_{v-reg}\left(m_0\right)$

具有T步的vSVF模型，其总损失为：
$$\begin{array}{c}{\sum }_{\tau =1}^T{\mathcal{L}}_v\left(I_0,I_1,{\Phi }_{(\tau )}^{-1},{\Phi }_{(\tau )}^{ts},m_0(\tau ),m_{0(\tau )}^{ts}\right)\text{ s.t.t. }\\ {\Phi }_{(\tau )}^{-1}(x,0)={\Phi }_{(\tau -1)}^{-1}(x,1)\\ {\left({\Phi }_{(\tau )}^{ts}\right)}^{-1}(x,0)={\left({\Phi }_{(\tau -1)}^{ts}\right)}^{-1}(x,1)\end{array}$$

三、训练

1. 多步仿射网络的训练

首先训练一个单步的网络，然后用它的参数来初始化多步的网络。在纵向的配准中，训练一个3步的仿射网络，而在测试的时候使用七步的网络；在跨物体配准中，训练一个5步的仿射网络，在测试的时候使用七步的网络。仿射对称因子${\lambda }_{as}$设为10。仿射正则因子是依赖于epoch的，其定义为：
$${\lambda }_{ar}:=\frac{C_{ar}{K}_{ar}}{K_{ar}+e^{n/K_{ar}}}$$
其中，$C_{ar}$是常数，$K_{ar}$用来控制衰减率，$n$是epoch数，$K_{ar}$设为4，$C_{ar}$设为10。

2. 动量生成网络的训练

使用10步和多高斯核（标准差为{0.05, 0.1, 0.15, 0.2, 0.25}）以及相关权重{j0.067, 0.133, 0.2, 0.267, 0.333}。在训练时都是训练两步，正则化因子${\lambda }_{vr}$设为10，对称因子${\lambda }_{vs}$设为$1e^{-4}$。每个实验有200个epoch，每个epoch有400个batch，一个batch包括一对图像。学习率为$5e^{-4}$，没60个epoch衰减为原来的0.5。使用mk-LNCC作为图像相似性指标，$(w,w)=\{(0,3,S/4),(0.7,S/2)\}$，其中$S$表示最小的图像维度，滑动窗口的步长设为$S/4$，采用因子为2的空洞卷积。

四、实验

1. 实验设置

数据集选用的是OAI（Osteoarthritis Initiative）MR数据集，预处理时将灰度值归一化，然后去除小于0.1%和大于99.9%的灰度值。所有图像重采样到$192\times 192\times 80$大小。将无标签的数据按7:3划分为训练集和验证集。使用Dice值来评价配准的结果。选用SyN，Demons，NiftyReg和VoxelMorph作为baseline。

2. 基于优化的多尺度仿射配准

开始时，对低分辨率的图像预测一个粗略的仿射参数，然后使用它作为更高分辨率的初始化参数。使用学习率为$1e^{-4}$的随机梯度下降优化器，三个图像尺寸分别为原图大小的$k\in \{0.25,0.5,1.0\}$，每个迭代200，200，50次。使用mk-LNCC作为相似性准则。在尺寸为1.0时，参数设为$(w,s)=\{(0.3,S_k/4),(0.7,S_k/2)\}$，在尺寸为0.5和0.25时，参数为$(w,s)=\{(1.0,S_k/2)\}$。

3. 基于优化的多尺度vSVF配准

采用仿射映射作为初始映射，采用和多尺度仿射配准相同的多尺度策略。采用LBGFS优化器，尺度为$\{0.25,0.5,1.0\}$，每个尺度迭代60次，使用mk-LNCC作为相似性指标。

4. 实验结果

上图是AVSM的结果图，前五行分别为源图像、目标图像、配准后的图像、具有变形网格的配准后图像和多步仿射配准的图像。后三行为源标签、目标标签、AVSM配准后的标签。

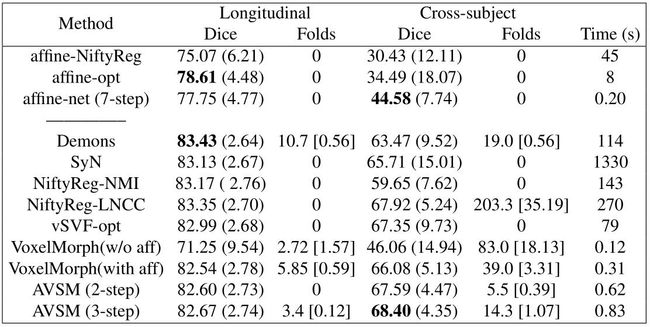
上图是不同配准方法的效果对比表，Affine-opt和vSVF-opt表示基于优化的多尺度仿射和vSVF配准。实验结果显示本文的AVSM模型在跨物体配准中的表现超过了其他方法，在纵向配准中，AVSM的效果也足够好，但是略差于基于优化的方法。这可能是因为形变是微妙的，或者源图像和目标图像非常相似，所以数值优化方法可能更好的对齐。

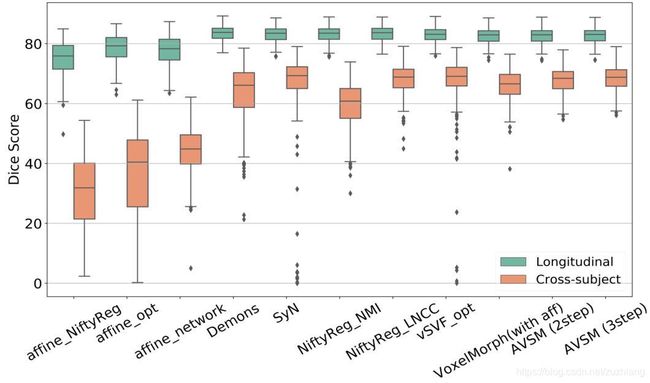
上图是更直观的表示，越高的越好。

当没有初始的仿射对齐时，VoxelMorph的效果不佳，只有进行了仿射对齐时，VoxelMorph才会达到很好的效果。

为了衡量变化映射的平滑性，使用雅克比行列式来估计：$J_{\varphi }(x):=\mid D{\varphi }^{-1}(x)|$，当$\{x:J_{\varphi }(x)<0\}$时，表示重叠。

上图是消融实验的结果表，在消融实验部分，发现引入多步和逆一致性提升了仿射配准的性能，相比于使用NCC，本文使用的mk-LNCC效果更好。

使用$\ln (\frac{1}{|V|}\Vert {\Phi }^{-1}\circ ({\Phi }^{ts}{)}^{-1}-id{\Vert }_2^2$来衡量对称性，其中$V$表示图像体积大小，$\Phi$表示通过仿射变换和可变形变换合成的映射。上图显示了有对称损失和无对称损失时的配准结果。

由于不同的方法对边界的处理不同，所以本文只对离边界10体素远的图像进行衡量。

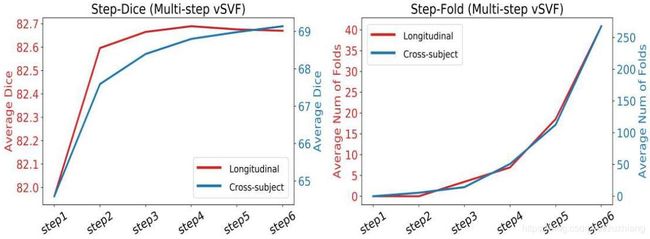
具有2步训练的多步vSVF配准结果，从左图可以看出效果随着step的增加而提升，右图显示同时重叠也增加。