第三课 BP神经网络

1 人工神经网络

在机器学习和认知科学中，人工神经网络（artificial neural networks ，ANNs)是受生物神经网络启发的一系列统计学习模型（动物的中枢神经系统，特别是大脑的中枢神经系统），用于估计或近似可依赖于大量输入且通常未知的函数。（通俗的讲就是需要输入大量样本数据进行训练学习，提取特征来进行统计分类）

1.1 人工神经元模型

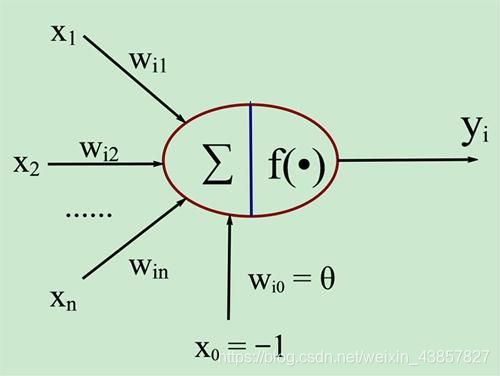
输入：X1-Xn是输入的数据；
权值：Wi1-Win是加权值；
Σ：是加权和，即输入*权值求和；
f(●)：映射函数，将加权和通过函数输出；
输出:y_i;
注意:X0和Wi0是为了方便输入的矩阵计算加的输入项；中间红色部分称为激活函数。

公式：
加权和+映射函数 ==> 输入和权值矩阵展开 ==> 向量表示

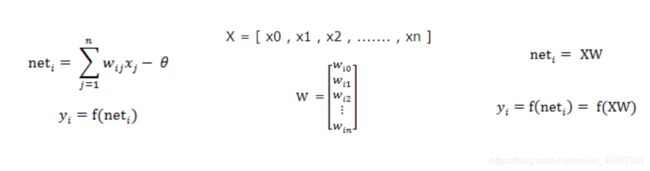
1.2 常见激活函数 y=f(x)

图形：

1.3 神经网络类型划分

• 按照连接方式，可以分为：前向神经网络 vs. 反馈（递归）神经网络
• 按照学习方式，可以分为：有监督学习神经网络 vs. 无监督学习神经网络
• 按照实现功能，可以分为：拟合（回归）神经网络 vs. 分类神经网络
  注意：BP神经网络是前向传播和有监督的神经网络

2 BP(Backpropagation)神经网络

名字叫反向传播但是是前向传播的神经网络。这里的反向是指学习方法不是连接方式，是指误差反向传播
反向传播是教授人工神经网络如何执行给定任务的常用方法。它是一种有监督的学习方法，是delta（δ）规则的推广。它要求模型知道或能够计算训练集中任何输入所需的输出。反向传播要求人工神经元（或“节点”）使用的激活函数是可微的。

2.1 学习算法

1、传播

• 通过神经网络对训练模式的输入进行正向传播，以产生传播的输出激活。
• 使用训练模式的目标，通过神经网络对传播输出激活的反向传播，以生成所有输出和隐藏神经元的增量。
  通俗的讲：首先通过输入和权值进行正向计算求得输出，然后用输出和理想的值进行计算求得误差(增量），将误差方向传播回去来修正每一层输入的权值的设定。

2、权值更新

• 将其输出增量和输入激活值相乘以获得权重的梯度。（梯度下降法）
• 通过从权重中减去一定比例来使权重朝梯度的相反方向移动

BP流程：
首先，通过输入层输入样本设设定的权值，来经过隐藏层的加权和计算，最后在输出层输出结果y，之后求y和目标值Z的差作为误差（经常使用差的平方和的二分之一），向后传播至隐藏层的第一层，求得每一层的误差，然后根据第一层的误差利用梯度下降法来计算与误差相连的权值，然后再正向修正所有隐藏层的权值，重新计算y值，当误差小于一定范围则计算结束。
先正向，再反向，再正向。
参考：http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html

使用反向传播训练多层神经网络的原理
使用有两个输入和一个输出的三层（隐藏层）神经网络，如下图所示：

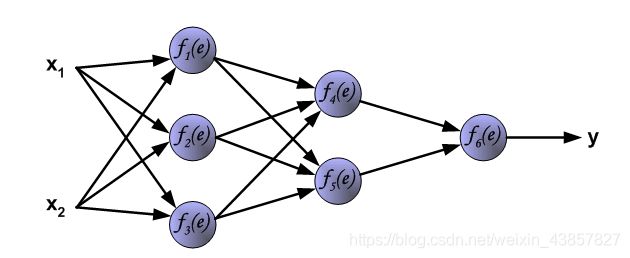
每个神经元由两个单元组成。第一单元将权重系数与输入信号的乘积相加。第二单元实现非线性函数，称为神经元激活函数。信号e为加法器输出信号（如果x2的值特别大，那么e受x2影响较大，x1可以忽略不计，所以要用归一化（后面介绍），因为x1和x2在实际中可能对e都有影响），y = f（e）为非线性元件的输出信号，也是神经元的输出信号。

要教神经网络，我们需要训练数据集。训练数据集由分配有相应目标（期望输出）z的输入信号（x 1和 x 2）组成。网络培训是一个反复的过程。在每次迭代中，使用来自训练数据集的新数据来修改节点的权重系数。修改是利用下面描述的算法计算：每个教学步骤与来自训练集迫使两个输入信号开始。在此阶段之后，我们可以确定每个网络层中每个神经元的输出信号值。下图显示了信号如何通过网络传播，符号W(xm)n 表示网络输入之间的连接权重输入层中的Xm和神经元n。符号y_n 代表神经元n的输出信号。

信号通过隐藏层传播。符号Wmn表示在下一层中神经元m的输出与神经元n的输入之间的连接权重 。

信号通过输出层传播。

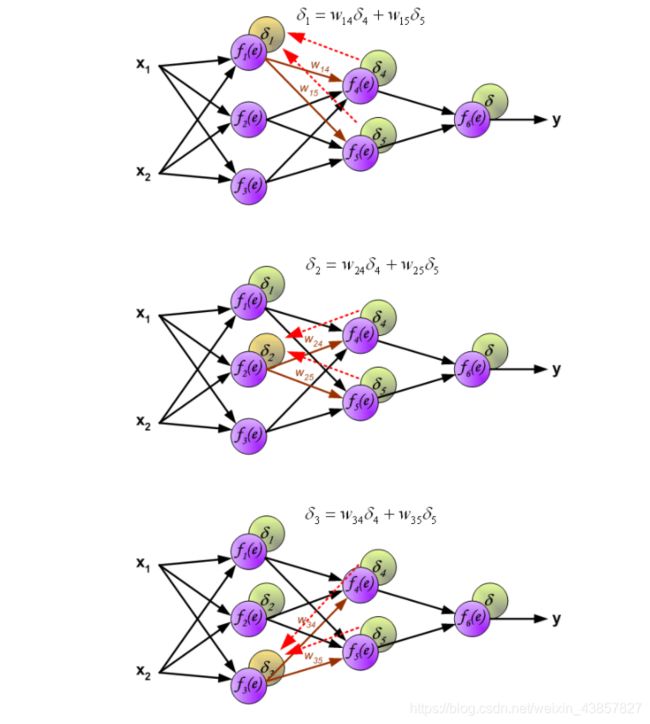
在下一个算法步骤中，将网络y的输出信号与在训练数据集中找到的所需输出值（目标）z进行比较。将该差称为输出层神经元的误差信号δ。

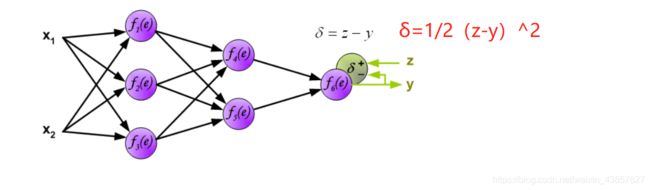
直接计算内部神经元的误差信号是不可能的（内部隐藏层无法计算），因为这些神经元的输出值是未知的。多年来，训练多人网络的有效方法一直未知。仅在80年代中期，才制定了反向传播算法。想法是将误差信号δ（在单个示教步骤中计算出）传播回所有神经元，这些输出信号被输入用于讨论的神经元。

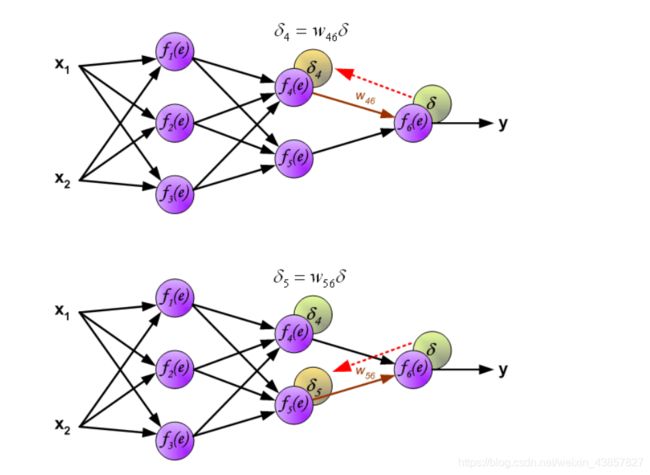
用于向后传播误差 的权重系数Wmn等于计算输出值时使用的权重系数。仅改变数据流的方向（信号从输出传播到输入一个接一个）。此技术适用于所有网络层。如果传播的错误来自少数神经元，则将其添加。插图如下：

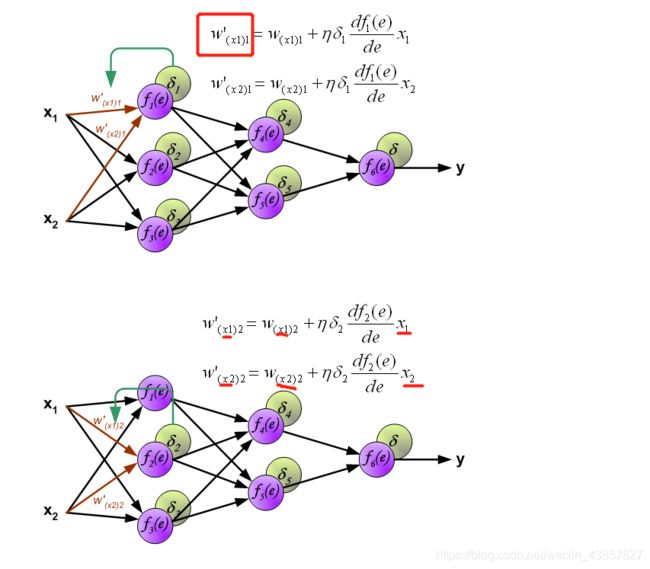
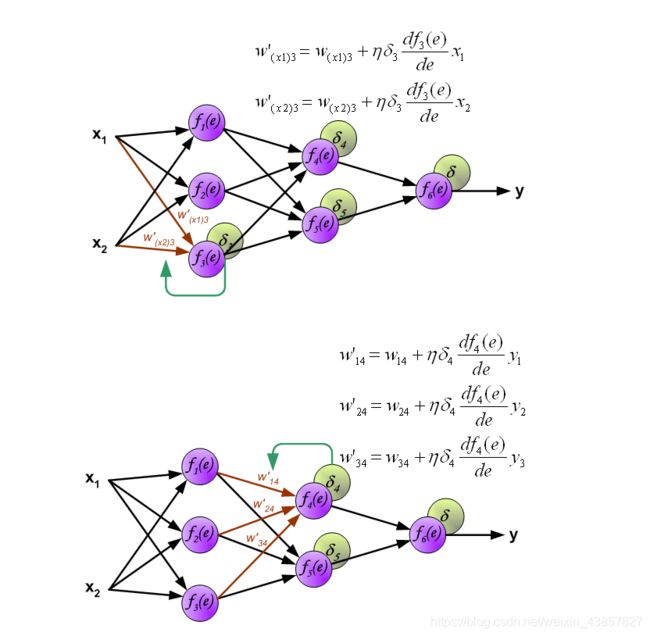
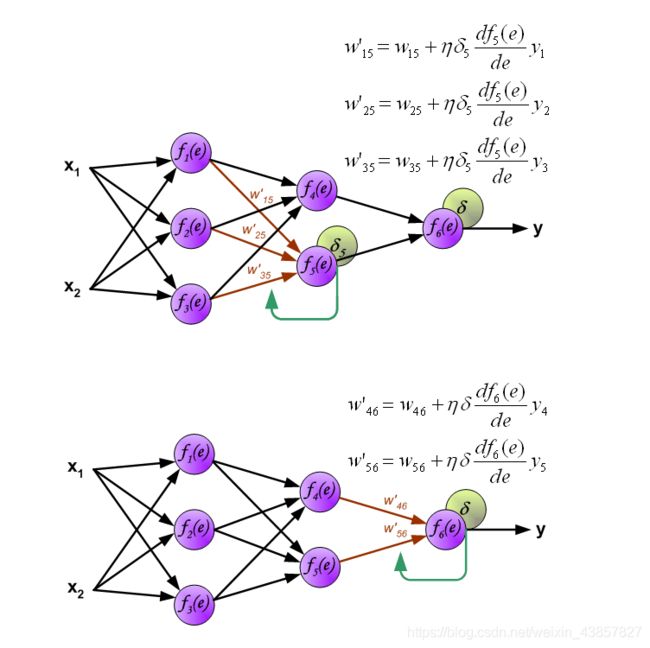
当计算每个神经元的误差信号时，可以修改每个神经元输入节点的权重系数。在下面的公式中， df(e) / de表示神经元激活函数的导数（权重已修改W(x1)1==>W’(x1)1）。
系数η影响网络教学速度。有几种技术可以选择此参数。第一种方法是使用较大的参数值开始教学过程。当建立权重系数时，该参数逐渐减小。第二种更复杂的方法以较小的参数值开始教学。在教学过程中，当教学时提前的参数被增加，然后在最后阶段再次下降。以低参数值开始教学过程可以确定权重系数符号。

3 数据归一化

目的：将数据映射到[0, 1]或[-1, 1]区间或其他的区间。

好处：
– 输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。
– 数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。
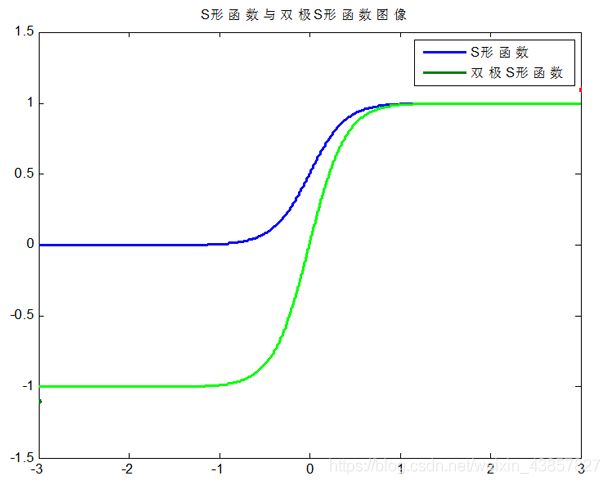
– 由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。
– S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时， f(100)与f(5)只相差0.0067。

归一化算法

y = ( x - min )/( max - min ) 或
y = 2 * ( x - min ) / ( max - min ) - 1

常用归一化函数：

mapminmax（）

3 newff（）函数

作用：创建信号前向误差反向传播网络；
用法： 输入层，输出层，隐藏层函数，权值，参数等

net = newff(P, T, [S1 S2...S(N-l)], {TF1 TF2...TFNl}, BTF, BLF, PF, IPF, OPF, DDF)

4 train（）函数

训练设置好的神经网络

[net, tr, Y, E, Pf, Af] = train(net, P, T, Pi, Ai)

5 sim（）函数

预测结果，仿真过程

[Y, Pf, Af, E, perf] = sim(net, P, Pi, Ai, T)

参数的影响

 隐含层神经元节点个数
 激活函数类型的选择
 学习率
 初始权值与阈值
有效避免影响的方法：
 样本多的时候：交叉验证（ cross validation）
 样本少的时候：留一法（ Leave one out, LOO）
 训练集（ training set）
 验证集（ validation set）
 测试集（ testing set）

仿真实验：

案例背景：利用近红外光谱分析方法(NIR)预测汽油中辛烷值的指标。
辛烷值是汽油最重要的品质指标，传统的实验室检测方法存在样品用量大、测试周期长和费用高等问题，不适用与生产控制，特别是在线测试，近红外光谱分析方法（NIR），作为一种快速分析方法，已经广泛应用于农业、制药、生物化工、石油产品等领域。其优越性是无损检测、低成本、无污染、能在线分析，更适合于生产和控制的需要。
针对采集得到的60组汽油样品，利用傅立叶近红外变换光谱仪对其扫描，扫描范围为900~1700nm，扫描间隔为2nm，每个样品的光谱曲线共含有401个波长点（变量或者特征60*401）。同时，利用传统实验室检测方法测定其辛烷值含量octance（标签）60*1。现要求利用RBF神经网络建立汽油样品近红外光谱与其辛烷值之间的关系的数学模型，并对模型的性能进行评价。

补充：matlab中randperm函数的用法和性能估算

将一列序号随机打乱，序号必须是整数。

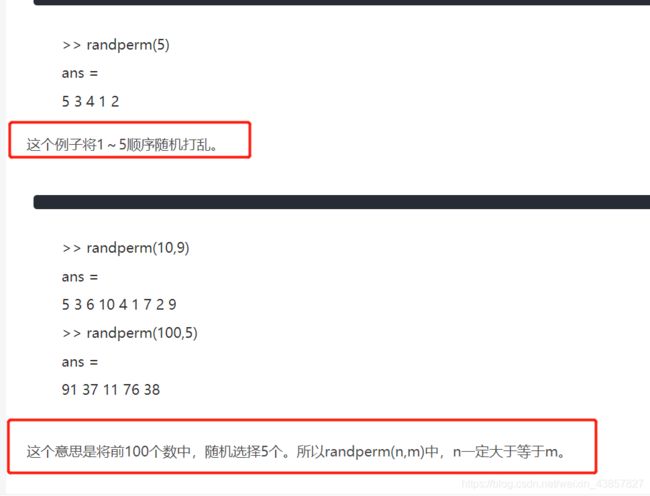
性能估算公式

实验：
流程图：

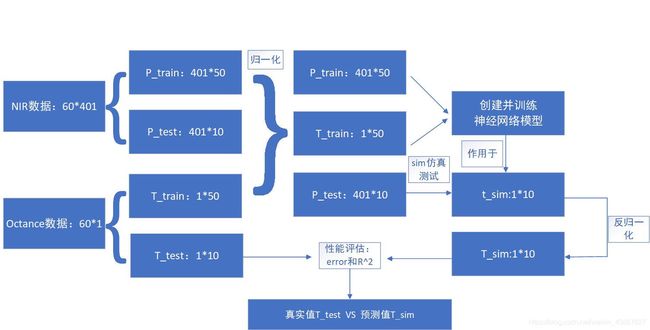
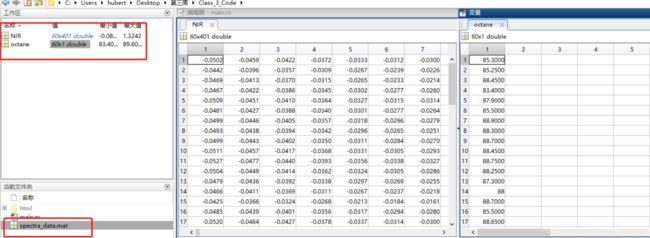
1、使用数据：spectra_data.mat octance：辛烷

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra_data.mat

2、命令框输入：

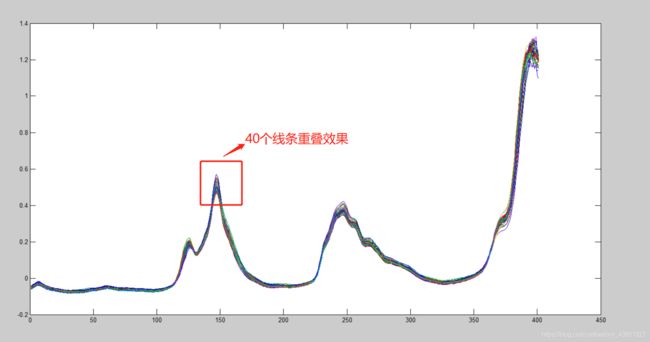
plot(NIR') %可得出401*60的图形实验

40个样本的不同波长点对应的NIR光谱大小。

3、随机划分50训练集和10测试集
NIR数据和octance都划分训练集和测试集 5:1

%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));%将60个样本随机排列，1*60
% 训练集——50个样本；% 测试集——10个样本
P_train = NIR(temp(1:50),:)';  %401*50
T_train = octane(temp(1:50),:)';  %1*50
P_test = NIR(temp(51:end),:)';  %401*10
T_test = octane(temp(51:end),:)';   % 1*10  目标值
N = size(P_test,2);  %测试集样本数N=10

4、数据归一化
保留一个T_test作为目标值

%% III. 数据归一化
[p_train, ps_input] = mapminmax(P_train,0,1);%ps_input是映射条件，p_train是归一化结果，归一结果是0-1之间
p_test = mapminmax('apply',P_test,ps_input);

[t_train, ps_output] = mapminmax(T_train,0,1);

5、神经网络创建
用p_train和t_train两个数据来创建神经网络net

%% IV. BP神经网络创建、训练及仿真测试
%%
% 1. 创建网络
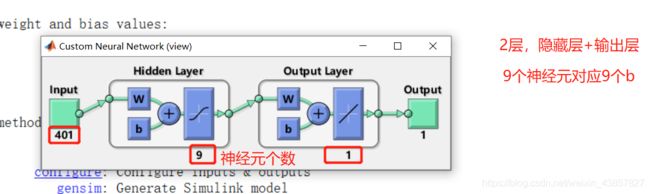
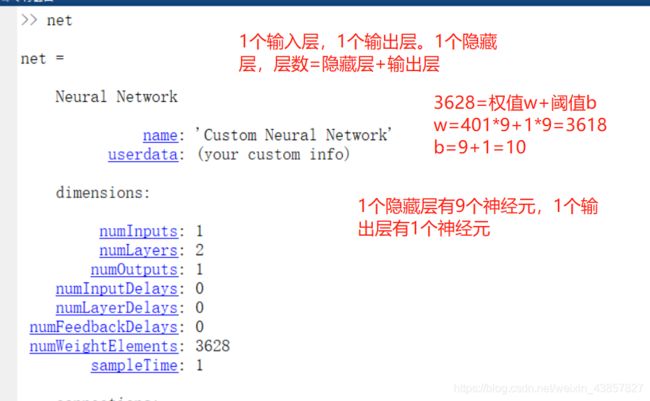
net = newff(p_train,t_train,9);  %输入p_train，输出t_train，9个神经元，单个隐藏层

%%
% 2. 设置训练参数
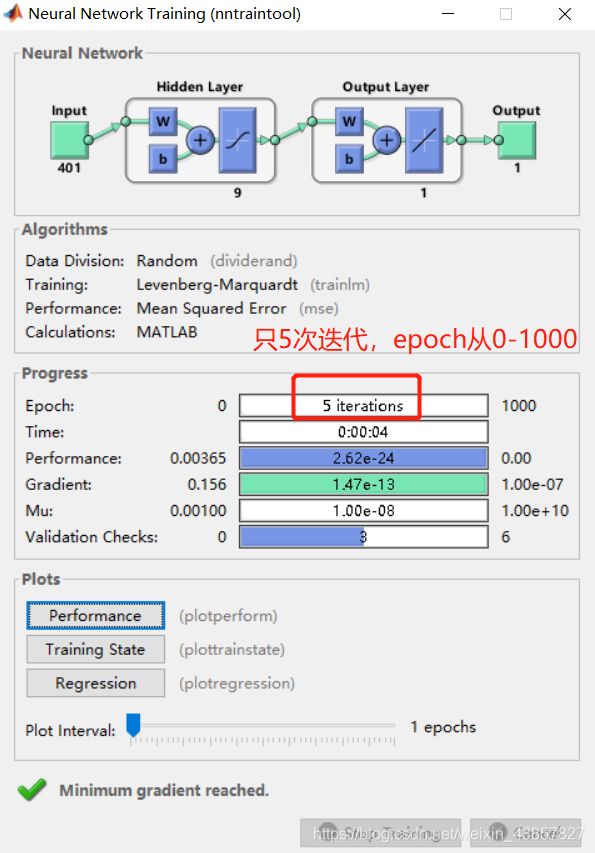
net.trainParam.epochs = 1000;  %迭代次数
net.trainParam.goal = 1e-3;%误差范围
net.trainParam.lr = 0.01;  %学习率

view(net)

net

6、训练网络

%%
% 3. 训练网络
net = train(net,p_train,t_train);

7、仿真评估

% 4. 仿真测试
t_sim = sim(net,p_test);  %返回测试样本的10个预测值1*10

%%
% 5. 数据反归一化
T_sim = mapminmax('reverse',t_sim,ps_output);

%% V. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;

%%
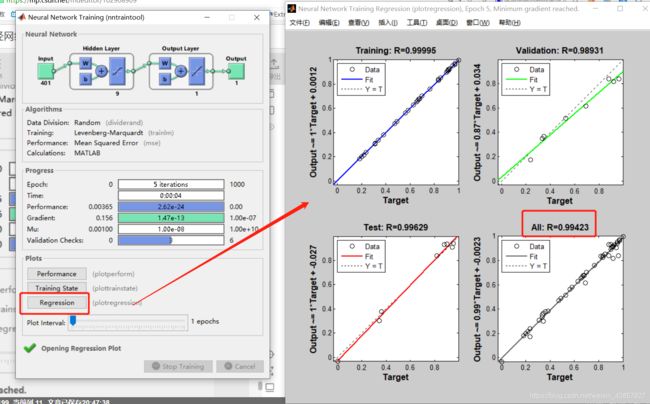
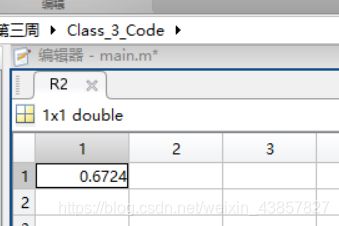
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 

%%
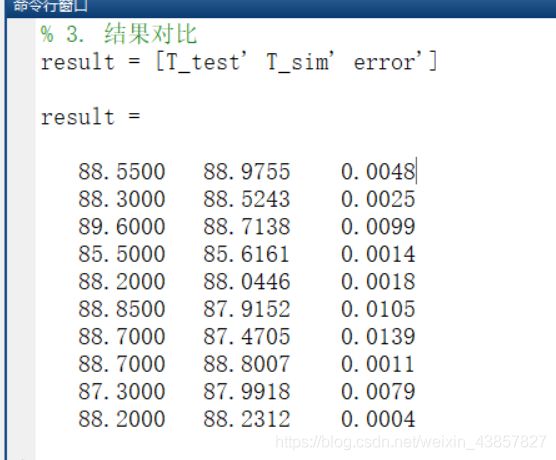
% 3. 结果对比
result = [T_test' T_sim' error']

R^2 就是一个值：

8、绘图
这不是用的准确率而是用的R^2来衡量模型的好坏。

%% VI. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

整体代码如下：

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra_data.mat

%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集——50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集——10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);

%% III. 数据归一化
[p_train, ps_input] = mapminmax(P_train,0,1);
p_test = mapminmax('apply',P_test,ps_input);

[t_train, ps_output] = mapminmax(T_train,0,1);

%% IV. BP神经网络创建、训练及仿真测试
%%
% 1. 创建网络
net = newff(p_train,t_train,9);

%%
% 2. 设置训练参数
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.lr = 0.01;

%%
% 3. 训练网络
net = train(net,p_train,t_train);

%%
% 4. 仿真测试
t_sim = sim(net,p_test);

%%
% 5. 数据反归一化
T_sim = mapminmax('reverse',t_sim,ps_output);

%% V. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;

%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 

%%
% 3. 结果对比
result = [T_test' T_sim' error']

%% VI. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)