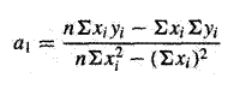曲线拟合——最小二乘拟合（附代码）

曲线拟合

先介绍一下拟合和插值的区别。插值，插值曲线必须经过所给定的插值点；拟合，拟合曲线不一定必须经过所给定的点。
（很多书里面对拟合、插值和逼近定义时讲，拟合包含：插值和逼近。这种说法对不对这里不做辩论，我只讲拟合和插值的方法与实现。）

拟合又包括一元函数和多元函数的拟合，通俗的讲，就是对一个变量（一维）和多个变量（多维）拟合的区别。对一个变量拟合叫曲线拟合，对两个变量的拟合可以称为曲面拟合。

本文主要讲一元函数的拟合（曲线拟合），包括直线的最小二乘拟合和多项式的最小二乘拟合；和多元函数的线性最小二乘拟合，对于非线性拟合会简单提及。

ps：关于非线性拟合，由于方法不太一样，会在另一篇文章中非线性回归——非线性函数最小二乘拟合讲到；关于函数插值，后续也会有更新。

1 一元函数的最小二乘拟合

1.1 线性回归（直线的最小二乘拟合）

1.1.1 直线的最佳拟合方法

根据一组二维坐标点$(x_1,y_1),(x_2,y_2),(x_3,y_3)\dots (x_n,y_n)$，将其进行拟合成一条直线。直线的数学表达式为：
$$y=a_0+a_{1}x$$
其中，$a_0$和$a_1$为系数，分别表示截距和斜率。

给定若干个点坐标，可以有很多种拟合成直线的方式，哪一种拟合效果最好呢？
如下图所示，给定7个点，随意给出了几种拟合直线，如黑色、蓝色、紫色三条直线，哪一条效果最理想？如何衡量拟合结果好坏呢？

这里我们给出一个定义：误差（或残差）。
误差（或残差），就是y的真实值与由线性方程预测的近似值$a_0+a_{1}x$之差。用$e$表示，可得：$e=y-a_0-a_{1}x$。

“最佳”拟合准则：通过数据点拟合一条“最佳”直线，使所有数据点的残差的平方和最小。

之所以选用残差的平方和最小，是因为：如果选残差的和最小，或者残差的绝对值之和最小，都会导致拟合效果不好，且结果不唯一。具体如下：

1. 如果选残差的和最小：如图(a)所示，它描述的是对两个点的直线拟合结果。显然，最佳拟合的结果就是连接这两个点的直线。然而，任何通过连线中点的直线(除了正好与连线垂直的直线外)都能使式(17.2)的结果为0，因为这样的直线与两个点的误差刚好大小相等但符号相反，所以刚好抵销了。
   
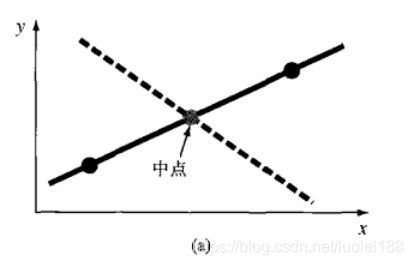
2. 如果残差的绝对值之和最小：图(b)说明了为什么这个准则还是不充分的。对于图中的四个点，位于两条虚线之间的任何直线，都会使上式中的绝对值之和最小。因此，使用这个准则也不能得到唯一的最优拟合直线。
   
   啰嗦了这么多，最后我们终于选定了将残差的平方和最小作为“最佳”拟合准则。
   也就是使Sr的值最小：
   

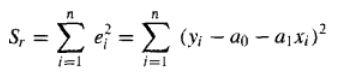
1.1.2 如何计算

那么怎么计算直线的系数$a_0$和$a_1$，才能保证直线最优呢。
方法如下：

令这些偏导数等于0，就可以得到残差平方和Sr的一个最小值。令这些偏导数等于0后，上面的方程
变为：


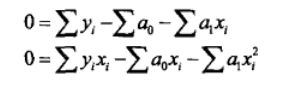
联立解方程组可得：

1.1.3 误差量化分析

残差的平方和Sr为：

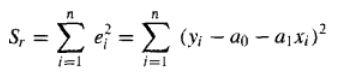
引入回归直线的“标准差”的概念和计算公式：

此外，还有“相关系数”也用来衡量直线拟合好坏（感兴趣可以查阅相关资料了解），如下：

其中，$S_t$表示因变量(在本例中为$y_i$）的均值的误差平方和，即$S_t={\sum }_{i=1}^n(y_i-\bar{y}{)}^2$，$\bar{y}$为$y_i$的平均值。

本文在最后附录里面给出了一元线性回归的伪代码及C++实现，可供参考。

1.2 多项式回归（多项式的最小二乘拟合）

1.2.1 推导过程和计算方法

最小二乘过程很容易推广到用史高阶多项式拟合数据的情况。例如，假设要拟合一个二次多项式:
$$y=a_0+a_{1}x+a_2{x}^2$$
残差平方和Sr计算为：
$$S_r=\sum _{i=1}^n(y_i-a_0-a_{1}x-a_2{x}^2{)}^2$$

对该式关于多项式的每个未知系数取导数，得到：

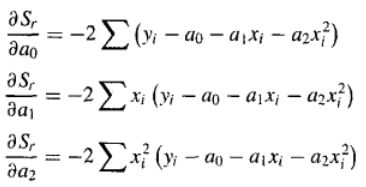
令导数为0，整理后得到：

方程组3个方程是线性的，有3个未知数:$a_0$, $a_1$和$a_2$，可以通过解方程组得到$a_0$, $a_1$和$a_2$的值。

二次多项式的情况很容易推广到m次多项式的情况：
$$y=a_0+a_{1}x+a_2{x}^2+\dots +a_m{x}^m$$
残差平方和Sr计算为：
$$S_r=\sum _{i=1}^n(y_i-a_0-a_{1}x-a_2{x}^2-\dots -a_m{x}^m{)}^2$$
同样求偏导令其为0，可以得到m+1个线性方程的方程组，联立解线性方程组可以得到系数$a_0$, $a_1$, $a_2$, … , $a_m$的值。

1.2.2 误差量化分析

同样，标准差的计算公式为:

“相关系数”计算公式如下：

其中，$S_t$表示因变量(在本例中为$y_i$）的均值的误差平方和，即$S_t={\sum }_{i=1}^n(y_i-\bar{y}{)}^2$，$\bar{y}$为$y_i$的平均值。

本文在最后附录里面给出了一元多项式回归的伪代码，可供参考。

2 多元函数的最小二乘拟合

2.1 多元线性回归

2.1.1 推导过程和计算方法

对于两个或多个自变量的情况，就是一个自变量的推广。对于两个自变量（二维）的情况，回归“直线”就变成了回归“平面”，如下图所示：

对于两个自变量的情况，设方程为:
$$y=a_0+a_1{x}_1+a_2{x}_2$$

同样的，残差平方和Sr计算为：
$$S_r=\sum _{i=1}^n(y_i-a_0-a_1{x}_1-a_2{x}_2{)}^2$$

令这些偏微分的值等于零，并采用矩阵形式表示，可得：

解该线性方程组可以得到系数$a_0$, $a_1$, $a_2$的值。

同样的，前面的二维情况很容易扩展到m维，即:
$$y=a_0+a_1{x}_1+a_2{x}_2+\dots +a_m{x}_m$$
也是同样的求偏微分，令其为0，解线性方程组，从而得到系数$a_0$, $a_1$, $a_2$, … , $a_m$的值。

2.1.2 误差量化分析

多元函数线性回归的标准差的计算公式，于一元函数多显示回归的一模一样；相关系数计算公式也一样。

标准差的计算公式:

“相关系数”计算公式：

其中，$S_t$表示因变量(在本例中为$y_i$）的均值的误差平方和，即$S_t={\sum }_{i=1}^n(y_i-\bar{y}{)}^2$，$\bar{y}$为$y_i$的平均值。

2.2 多元多项式回归？

很多人想着，既然有一元线性回归，有一元多项式回归，有多元线性回归，那是不是应该也有多元多项式回归？

答案却是，不存在的。或者说，大多数书里面是没有的。

细细思考一下，就知道，多元多项式回归？其实没那么简单：
如果说，
一元线性回归，有一个变量$x$，两个系数$a_0$, $a_1$；
一元多项式回归，有一个变量$x$，m+1个系数$a_0$, $a_1$, $a_2$, … , $a_m$；
多元线性回归，有m个变量$x_1$, $x_2$, $x_3$, … , $x_m$，m+1个系数$a_0$, $a_1$, $a_2$, … , $a_{m+1}$；
那么，对于多元线性回归，如果m个变量相互独立（就是不存在${x_i}^p{x_j}^q$这种形式），那么对于m个变量的n次多项式，也会存在m*n+1个系数，解方程组计算量庞大；而如果m个变量不相互独立，那就更。。。复杂了。

3 线性回归小结

线性最小二乘的一般矩阵形式

前面介绍了三种类型的回归方法：简单线性回归、多项式回归和多元线性回归。

事实上，这三种回归方法都属于一般形式的线性最小了二乘模型:
$$y=a_0+a_1{z}_1+a_2{z}_2+\dots +a_m{z}_m$$
其中，$z_1,z_2,\dots ,z_m$为m个基函数(basis function) 。

很容易看出，简单线性回归和多元线性回归归为这个模型；如果基函数是简单的单项式，即：$z_1=x^1,z_2=x^2,\dots ,z_m=x^m$，那么多项式回归也可以归为该类模型。

若将给定的n个点坐标代入$y=a_0+a_1{z}_1+a_2{z}_2+\dots +a_m{z}_m$，可得到n个线性方程组，表示为矩阵的形式：
$$Y=[Z]A$$

其中，m是模型中变量的个数，n是数据点的个数。

因为大多数情况下，n>m+1，所以[Z]不是一个方阵。因此，这个方程组属于过约束，不能直接求解。要计算相对条件下的最优解，就是使残差平方和最小的解。

而模型的残差平方和可以定义如下：

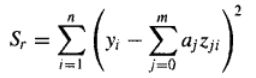
同样的，为了使Sr达到最小，需要对关于该式的每个系数$a_0$, $a_1$, $a_2$, … , $a_{m+1}$取偏导数，并令得到的每个方程等于0。于是可以表示成如下简洁的矩阵形式：

然后求解该方程组，即可得到系数$a_0$, $a_1$, $a_2$, … , $a_{m+1}$的值。
（感兴趣的可以用前面介绍的简单线性回归、多项式回归及多元线性的函数来验证。）

4* 非线性回归

4.1 非线性关系的线性化

非线性模型中有3种类型可以线性化：指数方程，幂方程，饱和增长率方程。分别如下：
1.指数方程:
$$y=a_1{e}^{a_{2}x}$$
2.幂方程:
$$y=a_1{x}^{a_2}$$
2.饱和增长率方程:
$$y=a_1\frac{x}{x+a_2}$$

对上述3种形式，可取自然对数将其线性化，结果如下：
指数方程取自然对数：$$lny=ln{a}_1+a_{2}x$$
lny与x的关系图是一条斜率为a_2，截距为lna_1的直线。

幂方程取10为底的对数：$$logy=log{a}_1+a_{2}logx$$
log y与log x的关系图是一条斜率为$a_2$，截距为$log{a}_1$的直线。

饱和增长率方程取自然对数：$$\frac{1}{y}=\frac{a_2}{a_1}\frac{1}{x}+\frac{1}{a_1}$$
于是，$\frac{1}{y}$与$\frac{1}{x}$的关系图是一条斜率为 $\frac{a_2}{a_1}$，截距为$\frac{1}{a_1}$的直线

然后，采用上面的线性回归的方法处理。

4.2* （真正的）非线性回归

对于如$$y=a_1(1-e^{-a_{2}x})$$形式的函数，是不能线性化的。
需要用牛顿迭代的方法来处理。具体的可参见：非线性回归——非线性函数最小二乘拟合。

5 附录（伪代码及C++实现）

5.1 一元线性回归算法

5.1.1 伪代码

5.1.2 C++实现

//直线的最小二乘拟合
LinearFitting(Vector <Point2d> points, double &lineDir, double &lineDis)
{
     
	int count = points.size();
	double sumX = 0, sumY = 0, sumXY = 0, sumSqrX =0, 
	for (int i = 0; i < count; i++)
	{
     
		sumX += points[i].x;
		sumY += points[i].y;
		sumXY += points[i].x * points[i].y;
		sumSqrX += points[i].x * points[i].x;
	}
	lineDir = (count*sumXY - sumX*sumY)/(count*sumSqrX - sumX*sumX);
	lineDis = (sumY - lineDir*sumX)/count;
	
	//计算回归相关系数
	double st = 0, sr = 0;
	double yMid = sumY/n;
	double xMid = sumX/n;
	for (int j = 0; j < count; j++)
	{
     
		st += (yi - yMid)*(yi - yMid);
		double tmpe = yi - lineDis - lineDir*xi;
		sr += tmpe *tmpe;
	}
	
	double Syx = sqrt（sr/count-2）；
	double R2 = (st - sr)/st;	
}

5.2 一元多项式回归算法

5.2.1 算法步骤

5.2.2 C++实现代码

（待更新）