关于SoftMax函数的一些介绍

前言

SoftMax函数是在机器学习中经常出现的，时常出现在输出层中。对于这个函数，大部分blog作者对于它介绍已经很完善了，包括如何玄学设计，如何使用等等，这里只是从数学来源上讨论下这个函数名字的来历，或者说数学的来源，为什么叫做Soft Max（有没有Hard Max）等等。

1.Soft Max的形式

Soft Max 函数，全名Soft Maximum函数。从机器学习过来的同学，更熟其形式为$$\sigma (\mathbf{z}{)}_j=\frac{e^{z_j}}{{\Sigma }_{k=1}^K{e}^{z_k}},（1）$$for$j=1,...,K$. 也被称为归一化指数函数，可以认为其是logistic 函数的一种一般化推广[1]（当k=2就是logistic函数），其将任意的K维实向量$\mathbf{z}$压缩到（squash）各分量为0-1上的K维实向量$\sigma (\mathbf{z})$，并且所有的分量加起来为1（为了保证映射后$\sigma (\mathbf{z}{)}_j$加在一起和为1,你可以理解成概率值）。在概率论里面将softmax函数的输出用来作为分类分布[2]（Categorical distribution)。这也就是softmax函数广泛应用于多类分类器，例如：softmax回归，多类线性判别分析，朴素贝叶斯分类，人工神经网络，以及，最近火热的各种深度学习（ai算法）等等。
相关数学性质详细介绍可以看参考文献[1]以及各类文献。本文在这里无意重复这些工作（例如softmax的求导优势），我们想讨论的是，这个函数的数学由来（而不是数学特性）。

2.大家都想知道的问题

实际上，很多人都想问的一个问题是，softmax函数中的soft如何解释，是不是有hard max，到底这里是怎么算的soft,文献[3][4][5]就是关于这个问题的一部分讨论。
一句话解释：实际上softmax对应的是（hard）max函数即$max(x_1,...,x_n)$。如果在此基础上用类似（1）构造一个n维的映射，你会发现，max函数将$x_i$中最大的数映射到1，其他的都映射到0，而softmax是对max函数的soft，如图。
其中红线是 $max(0,x)$， 蓝色线是$softmax(0,x)$.

Figure 1. “softmax function” vs “max function” from: Abhishek Patnia

至于为什么叫做softmax，其一是因为是Max函数的一种近似，其二是因为它光滑（smooth）近似了Max函数，注意它在0点的尖锐部分（不可导点）它光滑了函数。

3. Softmax详细解释

让我们从头开始说，这部分内容主要参考自文献[6],加上一部分自己的理解。主要讨论如下的一些问题。

1. 到底soft maximum是什么，他为什么被叫做这个名字
2. 怎么和maximum函数联系起来的
3. maximum函数的sharp edges是怎么个意思
4. soft maximum函数的优势有哪些
5. 怎么来控制soft 的程度

首先，我们给出两种函数的对比:
$$f(x,y)=max(x,y），(2.a)$$
$$g(x,y)=Log(e^x+e^y)，(2.b)$$
（可以扩展到n维形式）。其中a是我们常见的求两个数的最大值的函数形式，我们在这里为了方便对应，称其为（hard）maximum函数，b是 soft maximum函数（实际上（1）中的soft maximum是在机器学习在分类中的应用形式）。

其次，我们解释下为什么称b（soft maximum）函数是a（hard maximum）近似。假设b中$x>y$,$x$是略大的数，那么经过$e^x$放大后$e^x>>e^y$，将会远远的大于$e^y$(注，$x<0$时，不等关系不变，但是放大程度没有这么大）。因此，指数关系显著的放大了$x,y$之间的差距。如果$x$比$y$大很多，那么显然$e^x+e^y\approx e^x$, 所以soft maximum函数将会有$g(x,y)\approx log(e^x)=x$,此时，$g(x,y)=f(x,y)$，即soft maximum和hard maximum一样。

Figure 2. $e^x$的曲线

举个例子：如果求-3,1,4的最大值，hard maximum 毫无疑问时4，soft maximum值为4.04946。不够明显？不妨我们增加数之间距离，计算-3，1，8，soft maximum值8.00093。

下面通过几组图来理解下共识2.a和2.b的效果：

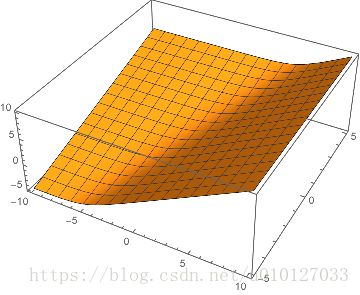
Figure 3. 三维图，左边soft，右边hard

Figure 4. 3D图沿着y=1的一个切面图，蓝色hard，橘色soft

注意到hard maximum在（1，1）这个点的那个尖锐部分（sharp edge），通俗来讲hard在这里不光滑，数学上来说这里不可导。因此在optimization计算中带来诸多不便。

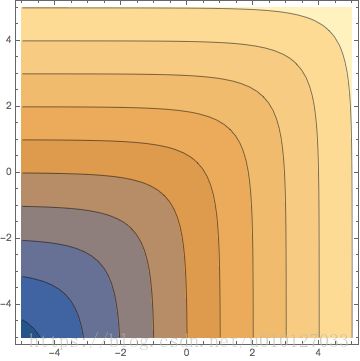
Figure 5. 等高线图，左边soft，右边hard

soft maximum是hard maximum函数的近似，并且同hard一样是凸函数，它的方向变化是连续的、光滑的、可导的（敲黑板，这是重点），并且实际上是可以求任意阶导数的。这些性质使其在凸优化中具有良好的特性，事实上最早引入soft maximum就是在优化学科中（optimization）。

注意到，soft maximum的近似程度实际上依赖于（两数之间的）scale（常翻译为尺度、这里应理解为比例、数量范围意思）。如果我们对$x,y$乘上比较大的一个常数，那么soft maximum将会更加接近hard maximum。例如$g(1,2)=2.31$，但是$g(10,20)=20.00004$。所以我们可以设计一个hardness因子在soft maximum函数中。例如：$$g(x,y:k)=\frac{log(e^{kx}+e^{ky})}{k}，(3)$$
通过调节k，可以自由的让soft maximum逼近maximum。而且对任意给定k，soft maximum函数依然是可导的，但是其导数大小随着k的增加而增加，极限为无穷大，此时soft 收敛到hard maximum。

4.如何计算[7]

虽然soft maximum的数学理论已经很清楚了，但是在实际计算中，还是会遇到一些问题，主要是因为计算机在进行浮点数计算的时候，存在overflow 和underflow问题，简而言之，就是计算$e^{1000},e^{-1000}$的时候，前者太大，计算机认为是无穷大，后者太小，计算机直接等于零。所以带来一系列奇怪的问题。

解决的方法也很简单，利用关系：$$log(e^x+e^y)=log(e^{x-k}+e^{y-k})+k，(4)$$式子证明很简单，这里就不多说了。你会发现通过这样的手段，假如我们选取k为x,y中较大的数。那么（4）中两项一个为0，一个为负数。自然就不会溢出了。

double SoftMaximum(double x, double y)
{
double maximum = max(x, y);
double minimum = min(x, y);
return maximum + log( 1.0 + exp(minimum - maximum) );
}

虽然其中“ exp(minimum - maximum) ”依然可能下溢到0，但是此时不影响我们返回maximum值。实际上从等价计算式子也能看出soft maximum函数的一些特点，首先，其一定大于hard 的结果；其次，当x,y两个值差异比较大的时候，soft和hard的结果越接近。当x，y的值很接近的时候，soft和hard的值偏离程度变大，特别是当x,y相等，偏离最远，近似程度最差。

关于在机器学习中应用soft maximum的帖子很多，例如：文献[8],这部分不是本文重点，大家详细参阅即可。

参考文献：
[1]https://en.wikipedia.org/wiki/Softmax_function
[2]https://en.wikipedia.org/wiki/Categorical_distribution
[3]https://stackoverflow.com/questions/30637909/how-to-interpret-the-soft-and-max-in-the-softmax-regression
[4]https://math.stackexchange.com/questions/1888141/why-is-the-softmax-function-called-that-way
[5]https://www.quora.com/Why-is-softmax-activate-function-called-softmax
[6]https://www.johndcook.com/blog/2010/01/13/soft-maximum/
[7]https://www.johndcook.com/blog/2010/01/20/how-to-compute-the-soft-maximum/
[8]https://zhuanlan.zhihu.com/p/25723112