TensorFlow 2.0深度学习算法实战 第十章 卷积神经网络

当前人工智能还未达到人类 5 岁水平，不过在感知方面进步飞快。未来在机器语音、视觉识别领域，五到十年内超越人类没有悬念。−沈向洋

我们已经介绍了神经网络的基础理论、TensorFlow 的使用方法以及最基本的全连接层网络模型，对神经网络有了较为全面、深入的理解。但是对于深度学习，我们尚存一丝疑惑。深度学习的深度是指网络的层数较深，一般有 5 层以上，而目前所介绍的神经网络层数大都实现为 5 层之内。那么深度学习与神经网络到底有什么区别和联系呢？

本质上深度学习和神经网络所指代的是同一类算法。1980 年代，基于生物神经元数学模型的多层感知机(Multi-Layer Perceptron，简称 MLP)实现的网络模型就被叫作神经网络。由于当时的计算能力受限、数据规模较小等因素，神经网络一般只能训练到很少的层数，我们把这种规模的神经网络叫做浅层神经网络(Shallow Neural Network)。浅层神经网络不太容易轻松提取数据的高层特征，表达能力一般，虽然在诸如数字图片识别等简单任务上取得不错效果，但很快被 1990 年代新提出的支持向量机所超越。

加拿大多伦多大学教授 Geoffrey Hinton 长期坚持神经网络的研究，但由于当时支持向量机的流行，神经网络相关的研究工作遇到了重重阻碍。2006 年，Geoffrey Hinton 提出了一种逐层预训练的算法，可以有效地初始化 Deep Belief Networks(DBN)网络，从而使得训练大规模、深层数(上百万的参数量)的神经网络成为可能。在论文中，GeoffreyHinton 把深层的神经网络叫做 Deep Neural Network，这一块的研究也因此称为 DeepLearning(深度学习)。由此看来，深度学习和神经网络本质上指代大体一致，深度学习更侧重于深层次的神经网络的相关研究。深度学习的“深度”将在本章的相关网络模型上得到淋漓尽致的体现。

在学习更深层次的网络模型之前，首先我们来探讨这样一个问题：1980 年代时神经网络的理论研究基本已经到位，为什么却没能充分发掘出深层网络的巨大潜力？通过对这个问题的讨论，我们引出本章的核心内容：卷积神经网络。这也是层数可以轻松达到上百层的一类神经网络。

10.1 全连接网络的问题

首先我们来分析全连接网络存在的问题。考虑一个简单的 4 层全连接层网络，输入是28 × 28打平后为 784 节点的手写数字图片向量，中间三个隐藏层的节点数都是 256，输出层的节点数是 10，如图 10.1 所示。

通过 TensorFlow 快速地搭建此网络模型，添加 4 个 Dense 层，并使用 Sequential 容器封装为一个网络对象：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,Sequential,losses,optimizers,datasets

# 创建4层全连接网络
model=keras.Sequential([
    layers.Dense(256,activation='relu'),
    lsyers.Dense(256,activation='relu'),
    layers.Dense(256,activation='relu'),
    layers.Dense(10),
])
#build模型，并打印模型信息
model.build(input_shape=(4,784))
model.summary()

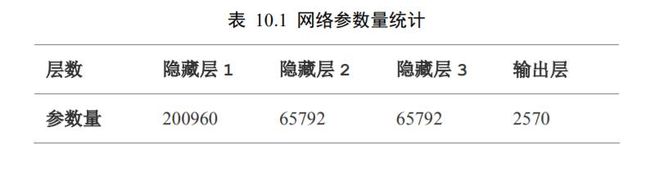
利用 summary()函数打印出模型每一层的参数量统计结果，如表 10.1 所示。网络的参数量是怎么计算的呢？对于每一条连接线的权值标量，视作一个参数，因此对输入节点数为，输出节点数为的全连接层来说，张量包含的参数量共有 ∙ 个，向量包含的参数量有个，则全连接层的总参数量为 ∙ + 。以第一层为例，输入特征长度为 784，输出特征长度为 256，当前层的参数量为 784 ∙ 256 + 256= 200960 ，同样的方法可以计算第二、三、四层的参数量分别为： 65792、 65792、5702 ，总参数量约 34 万个。

在计算机中，如果将单个权值保存为 float 类型的变量，至少需要占用 4 个字节内存(Python 语言中float 占用内存更多)，那么 34 万个网络参数至少需要约 1.34MB 内存。也就是说，单就存储网络的参数就需要 1.34MB 内存，实际上，网络的训练过程中还需要缓存计算图模型、梯度信息、输入和中间计算结果等，其中梯度相关运算占用资源非常多。

那么训练这样一个网络到底需要多少内存呢？我们可以在现代 GPU 设备上简单模拟一下资源消耗情况。在 TensorFlow 中，如果不设置显存占用方式，那么默认会占用全部显存。这里将 TensorFlow 的显存使用方式设置为按需分配，观测其真实占用的 GPU 显存资源情况，代码如下：

#获取所有GPU设备列表
gpus=tf.config.experimental.list_physical_devices('GPU')
if gpus:
    try:
        # 设置GPU显存设备为按需分配，增长式
        for gpu in gpus:
            tf.config.experimental.set_memory_growth(gpu,True)
    except RuntimeError as e:
        # 异常处理
        print(e)

上述代码插入在 TensorFlow 库导入后、模型创建前的位置，通过tf.config.experimental.set_memory_growth(gpu, True)设置 TensorFlow 按需申请显存资源，这样 TensorFlow 占用的显存大小即为运算需要的数量。在 Batch Size 设置为 32 的情况下，x训练时我们观察到显存占用了约 708MB，内存占用约 870MB。由于现代深度学习框架设计考量不一样，这个数字仅做参考。即便如此，我们也能感受到 4 层的全连接层的计算代价并不小。

回到 1980 年代，1.3MB 的网络参数量是什么概念呢？1989 年，Yann LeCun 在手写邮政编码识别的论文中采用了一台 256KB 内存的计算机实现了他的算法，这台计算机还配备了一块 AT&T DSP-32C 的 DSP 计算卡(浮点数计算能力约为 25MFLOPS)。对于 1.3MB的网络参数，256KB 内存的计算机连网络参数都尚且装载不下，更别提网络训练了。由此可见，全连接层较高的内存占用量严重限制了神经网络朝着更大规模、更深层数方向的发展。

10.1.1 局部相关性

接下来我们探索如何避免全连接网络的参数量过大的缺陷。为了便于讨论，我们以图片类型数据为输入的场景为例。对于 2D 的图片数据，在进入全连接层之前，需要将矩阵数据打平成 1D 向量，然后每个像素点与每个输出节点两两相连，我们把连接关系非常形象地对应到图片的像素位置上，如图 10.2 所示。

可以看出，网络层的每个输出节点都与所有的输入节点相连接，用于提取所有输入节点的特征信息，这种稠密的连接方式是全连接层参数量大、计算代价高的根本原因。全连接层也称为稠密连接层(Dense Layer)，输出与输入的关系为：

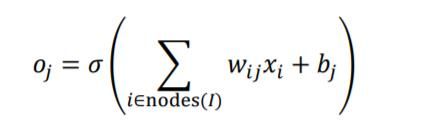
其中nodes()表示 I 层的节点集合。

那么，输出节点是否有必要和全部的输入节点相连接呢？有没有一种近似的简化模型呢？我们可以分析输入节点对输出节点的重要性分布，仅考虑较重要的一部分输入节点，而抛弃重要性较低的部分节点，这样输出节点只需要与部分输入节点相连接，表达为：

其中top($I,j,k$)表示 $I$ 层中对于 $J$ 层中的$j$号节点重要性最高的前$k$个节点集合。通过这种方式，可以把全连接层的$\Vert I\Vert \bullet \Vert J\Vert$个权值连接减少到$k\bullet \Vert J\Vert$个，其中$\Vert I\Vert$、$\Vert J\Vert$分布表示 $I$、$J$ 层的节点数量。

那么问题就转变为探索$I$层输入节点对于$j$号输出节点的重要性分布。然而找出每个中间节点的重要性分布是件非常困难的事情，我们可以针对于具体问题，利用先验知识把这个问题进一步简化。

在现实生活中，存在着大量以位置或距离作为重要性分布衡量标准的数据，比如和自己居住更近的人更有可能对自己影响更大(位置相关)，股票的走势预测应该更加关注近段时间的数据趋势(时间相关)，图片每个像素点和周边像素点的关联度更大(位置相关)。

以2D 图片数据为例，如果简单地认为与当前像素欧式距离(Euclidean Distance)小于和等于$\frac{k}{\sqrt{2}}$的像素点重要性较高，欧式距离大于$\frac{k}{\sqrt{2}}$到像素点重要性较低，那么我们就很轻松地简化了每个像素点的重要性分布问题。

如图 10.3 所示，以实心网格所在的像素为参考点，它周边欧式距离小于或等于$\frac{k}{\sqrt{2}}$的像素点以矩形网格表示，网格内的像素点重要性较高，网格外的像素点较低。这个高宽为的窗口称为感受野(Receptive Field)，它表了每个像素对于中心像素的重要性分布情况，网格内的像素才会被考虑，网格外的像素对于中心像素会被简单地忽略。

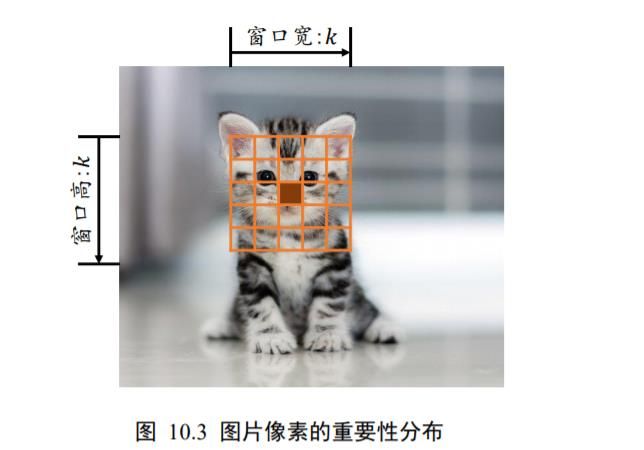
这种基于距离的重要性分布假设特性称为局部相关性，它只关注和自己距离较近的部分节点，而忽略距离较远的节点。在这种重要性分布假设下，全连接层的连接模式变成了如图 10.4 所示，输出节点只与以为中心的局部区域(感受野)相连接，与其它像素无连接。

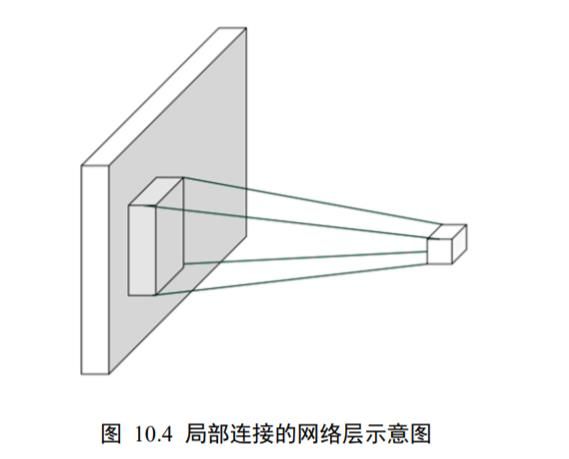
利用局部相关性的思想，我们把感受野窗口的高、宽记为(感受野的高、宽可以不相等，为了便与表达，这里只讨论高宽相等的情况)，当前位置的节点与大小为的窗口内的所有像素相连接，与窗口外的其它像素点无关，此时网络层的输入输出关系表达如下：

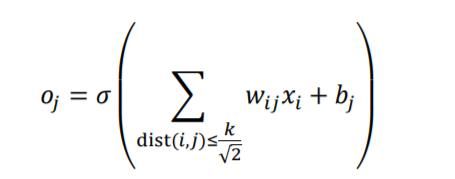
其中dist( )表示节点、之间的欧式距离。

10.1.2 权值共享

每个输出节点仅与感受野区域内 × 个输入节点相连接，输出层节点数为$\Vert J\Vert$，则当前层的参数量为 × × $\Vert J\Vert$，相对于全连接层的$\Vert I\Vert$ ×$\Vert J\Vert$，考虑到一般取值较小，如 1、3、5 等， × ≪ $\Vert I\Vert$，因此成功地将参数量减少了很多。

能否再将参数量进一步减少，比如只需要 × 个参数即可完成当前层的计算？答案是肯定的，通过权值共享的思想，对于每个输出节点$o_j$，均使用相同的权值矩阵，那么无论输出节点的数量$\Vert J\Vert$是多少，网络层的参数量总是 × 。如图 10.5 所示，在计算左上角位置的输出像素时，使用权值矩阵：

与对应感受野内部的像素相乘累加，作为左上角像素的输出值；在计算右下方感受野区域时，共享权值参数，即使用相同的权值参数相乘累加，得到右下角像素的输出值，此时网络层的参数量只有3 × 3 = 9个，且与输入、输出节点数无关。

通过运用局部相关性和权值共享的思想，我们成功把网络的参数量从$\Vert I\Vert \times \Vert J\Vert$减少到$K\times k$(准确地说，是在单输入通道、单卷积核的条件下)。这种共享权值的“局部连接层”网络其实就是卷积神经网络。接下来我们将从数学角度介绍卷积运算，进而正式学习卷积神经网络的原理与计算方法。

10.1.3 卷积运算

在局部相关性的先验下，我们提出了简化的“局部连接层”，对于窗口 × 内的所有像素，采用权值相乘累加的方式提取特征信息，每个输出节点提取对应感受野区域的特征信息。这种运算其实是信号处理领域的一种标准运算：离散卷积运算。离散卷积运算在计算机视觉中有着广泛的应用，这里给出卷积神经网络层从数学角度的阐述。

在信号处理领域，1D 连续信号的卷积运算被定义两个函数的积分：函数()、函数()，其中()经过了翻转(−)和平移后变成( − )。卷积的“卷”是指翻转平移操作，“积”是指积分运算，1D 连续卷积定义为：
$$(f\otimes g)(n)={\int }_{-\infty }^{\infty }f(\tau )g(n-\tau )\mathrm{d}\tau$$
离散卷积将积分运算换成累加运算：
$$(f\otimes g)(n)=\sum _{\tau =-\infty }^{\infty }f(\tau )g(n-\tau )$$
至于卷积为什么要这么定义，限于篇幅不做深入阐述。我们重点介绍 2D 离散卷积运算。在计算机视觉中，卷积运算基于 2D 图片函数(,)和 2D 卷积核(,)，其中(,)和(,)仅在各自窗口有效区域存在值，其它区域视为 0，如图 10.6 所示。此时的 2D 离散卷积定义为：
$$[f\otimes g](m,n)=\sum _{i=-\infty }^{\infty }\sum _{j=-\infty }^{\infty }f(i,j)g(m-i,n-j)$$

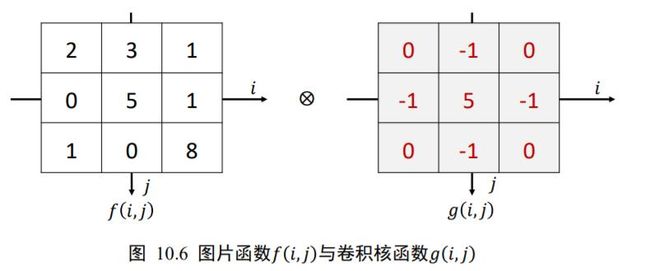
我们来详细介绍 2D 离散卷积运算。首先，将卷积核( , )函数翻转(沿着和方向各翻转一次)，变成(− ,−)。当( ,) = (−1, −1 )时，(− 1− ,− 1− )表示卷积核函数翻转后再向左、向上各平移一个单元，此时：
$$\begin{array}{rl}[f\otimes g](-1,-1)& =\sum _{i=-\infty }^{\infty }\sum _{j=-\infty }^{\infty }f(i,j)g(-1-i,-1-j)\\ & =\sum _{i\in [-1,1]}\sum _{j\in [-1,1]}f(i,j)g(-1-i,-1-j)\end{array}$$
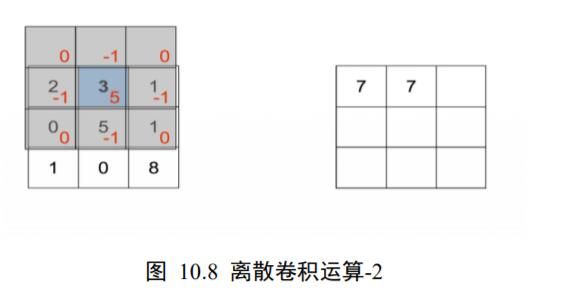
2D 函数只在 ∈[-1,1] , ∈[-1,1] 存在有效值，其它位置为 0。按照计算公式，我们可以得到 ⨂ ( 0,−1 ) =7 ，如下图 10.7 所示：

同样的方法，( ,) = ( 0,−1 )时：
$$[f\otimes g](0,-1)=\sum _{i\in [-1,1]j\in [-1,1]}f(i,j)g(0-i,-1-j)$$
即卷积核翻转后再向上平移一个单元后对应位置相乘累加， ⨂ (0, −1 ) =7 ，如图 10.8所示。

即卷积核翻转后再向右、向上各平移一个单元后对应位置相乘累加， ⨂ (1, −1 ) = 1，如图 10.9 所示。

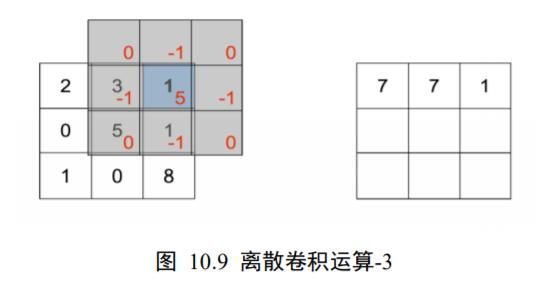
当( ) = (−1,0 )时：
$$[f\otimes g](-1,0)=\sum _{i\in [-1,1]j\in [-1,1]}f(i,j)g(-1-i,-j)$$
即卷积核翻转后再向左平移一个单元后对应位置相乘累加， ⨂ (−1,0 ) = 1，如图 10.10所示。

按照此种方式循环计算，可以计算出函数 ⨂ ( ) ∈[-1,1] , ∈[-1,1]的所有值，如下图 10.11 所示。

至此，我们成功完成图片函数与卷积核函数的卷积运算，得到一个新的特征图。

回顾“权值相乘累加”的运算，我们把它记为 [ ∙ ] ( ,)：
$$[f\cdot g](m,n)=\sum _{i\in [-w/2,w/2]}\sum _{j\in [-h/2,h/2]}f(i,j)g(i-m,j-n)$$
仔细比较它与标准的 2D 卷积运算不难发现，在“权值相乘累加”中的卷积核函数( ,)，并没有经过翻转。只不过对于神经网络来说，目标是学到一个函数( ,)使得ℒ越小越好，至于(, )是不是恰好就是卷积运算中定义的“卷积核”函数并不十分重要，因为我们并不会直接利用它。在深度学习中，函数( ,)统一称为卷积核(Kernel)，有时也叫 Filter、Weight 等。由于始终使用( ,)函数完成卷积运算，卷积运算其实已经实现了权值共享的思想。

我们来小结 2D 离散卷积运算流程：每次通过移动卷积核，并与图片对应位置处的感受野像素相乘累加，得到此位置的输出值。卷积核即是行、列为大小的权值矩阵，对应到特征图上大小为的窗口即为感受野，感受野与权值矩阵相乘累加，得到此位置的输出值。通过权值共享，我们从左上方逐步向右、向下移动卷积核，提取每个位置上的像素特征，直至最右下方，完成卷积运算。可以看出，两种理解方式殊途同归，从数学角度理解，卷积神经网络即是完成了 2D 函数的离散卷积运算；从局部相关与权值共享角度理解，也能得到一样的效果。通过这两种角度，我们既能直观理解卷积神经网络的计算流程，又能严谨地从数学角度进行推导。正是基于卷积运算，卷积神经网络才能如此命名。

在计算机视觉领域，2D 卷积运算能够提取数据的有用特征，通过特定的卷积核与输入图片进行卷积运算，获得不同特征的输出图片，如下表 10.2 所示，列举了一些常见的卷积核及其效果样片。

10.2 卷积神经网络

卷积神经网络通过充分利用局部相关性和权值共享的思想，大大地减少了网络的参数量，从而提高训练效率，更容易实现超大规模的深层网络。2012 年，加拿大多伦多大学Alex Krizhevsky 将深层卷积神经网络应用在大规模图片识别挑战赛 ILSVRC-2012 上，在ImageNet 数据集上取得了 15.3% 的 Top-5 错误率，排名第一，相对于第二名在 Top-5 错误率上降低了 10.9%，这一巨大突破引起了业界强烈关注，卷积神经网络迅速成为计算机视觉领域的新宠，随后在一系列的任务中，基于卷积神经网络的形形色色的模型相继被提出，并在原有的性能上取得了巨大提升。

现在我们来介绍卷积神经网络层的具体计算流程。以 2D 图片数据为例，卷积层接受高、宽分别为ℎ、，通道数为$c_{in}$的输入特征图，在$c_{out}$个高、宽都为，通道数为$c_{in}$的卷积核作用下，生成高、宽分别为ℎ′、′，通道数为$c_{out}$的特征图输出。需要注意的是，卷积核的高宽可以不等，为了简化讨论，这里仅讨论高宽都为的情况，之后可以轻松推广到高、宽不等的情况。

我们首先从单通道输入、单卷积核的情况开始讨论，然后推广至多通道输入、单卷积核，最后讨论最常用，也是最复杂的多通道输入、多个卷积核的卷积层实现。

10.2.1 单通道输入和单卷积核

首先讨论单通道输入$c_{in}$=1 ，如灰度图片只有灰度值一个通道，单个卷积核$c_{out}$=1的情况。以输入为 5×5 的矩阵，卷积核为3 × 3的矩阵为例，如下图 10.12 所示。与卷积核同大小的感受野(输入上方的绿色方框)首先移动至输入最左上方，选中输入上3 × 3的感受野元素，与卷积核(图片中间3 × 3方框)对应元素相乘：

⨀符号表示哈达马积(Hadamard Product)，即矩阵的对应元素相乘，它与矩阵相乘符号@是矩阵的二种最为常见的运算形式。运算后得到3 × 3的矩阵，这 9 个数值全部相加：
$$-1-1+0-1+2+6+0-2+4=7$$
得到标量 7，写入输出矩阵第一行、第一列的位置，如图 10.12 所示。

完成第一个感受野区域的特征提取后，感受野窗口向右移动一个步长单位(Strides，记为，默认为 1)，选中图 10.13 中绿色方框中的 9 个感受野元素，按照同样的计算方法，与卷积核对应元素相乘累加，得到输出 10，写入第一行、第二列位置。

感受野窗口再次向右移动一个步长单位，选中图 10.14 中绿色方框中的元素，并与卷积核相乘累加，得到输出 3，并写入输出的第一行、第三列位置，如图 10.14 所示。

此时感受野已经移动至输入的有效像素的最右边，无法向右边继续移动(在不填充无效元素的情况下），因此感受野窗口向下移动一个步长单位( = 1)，并回到当前行的行首位置，继续选中新的感受野元素区域，如图 10.15 所示，与卷积核运算得到输出-1。此时的感受野由于经过向下移动一个步长单位，因此输出值-1 写入第二行、第一列位置。

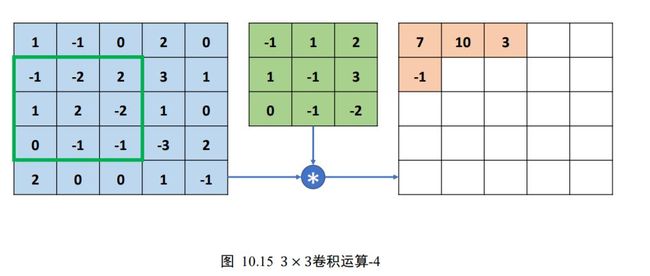
按照上述方法，每次感受野向右移动 = 1个步长单位，若超出输入边界，则向下移动 =1 个步长单位，并回到行首，直到感受野移动至最右边、最下方位置，如下图 10.16 所示。

每次选中的感受野区域元素，和卷积核对应元素相乘累加，并写入输出的对应位置。最终输出我们得到一个3 × 3的矩阵，比输入 5×5 略小，这是因为感受野不能超出元素边界的缘故。可以观察到，卷积运算的输出矩阵大小由卷积核的大小，输入的高宽ℎ/，移动步长，是否填充等因素共同决定。这里为了演示计算过程，预绘制了一个与输入等大小的网格，并不表示输出高宽为 5×5 ，这里的实际输出高宽只有3 × 3。

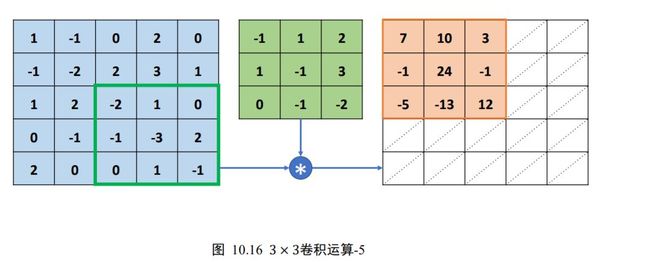
现在我们已经介绍了单通道输入、单个卷积核的运算流程。实际的神经网络输入通道数量往往较多，接下来我们将学习多通道输入、单个卷积核的卷积运算方法。

10.2.2 多通道输入和单卷积核

多通道输入的卷积层更为常见，比如彩色的图片包含了 R/G/B 三个通道，每个通道上面的像素值表示 R/G/B 色彩的强度。

下面我们以 3 通道输入、单个卷积核为例，将单通道输入的卷积运算方法推广到多通道的情况。如图 10.17 中所示，每行的最左边 5×5 的矩阵表示输入的 1~3 通道，第 2 列的3 × 3矩阵分别表示卷积核的 1~3 通道，第 3 列的矩阵表示当前通道上运算结果的中间矩阵，最右边一个矩阵表示卷积层运算的最终输出。

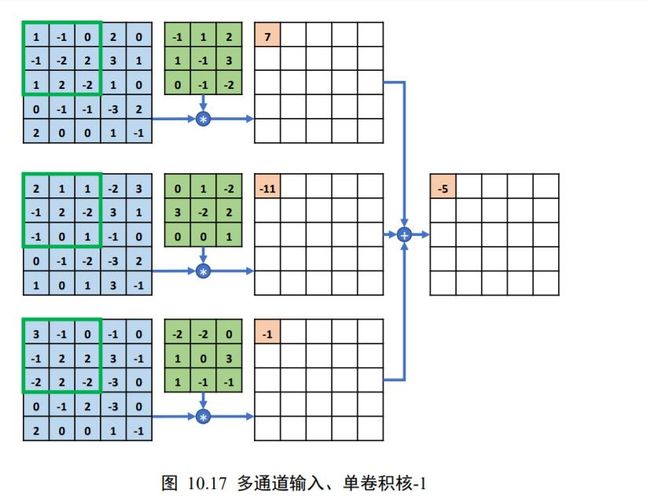
在多通道输入的情况下，卷积核的通道数需要和输入的通道数量相匹配，卷积核的第个通道和的第个通道运算，得到第个中间矩阵，此时可以视为单通道输入与单卷积核的情况，所有通道的中间矩阵对应元素再次相加，作为最终输出。

具体的计算流程如下：在初始状态，如图 10.17 所示，每个通道上面的感受野窗口同步落在对应通道上面的最左边、最上方位置，每个通道上感受野区域元素与卷积核对应通道上面的矩阵相乘累加，分别得到三个通道上面的输出 7、-11、-1 的中间变量，这些中间变量相加得到输出-5，写入对应位置。

随后，感受野窗口同步在的每个通道上向右移动 = 1个步长单位，此时感受野区域元素如下图 10.18 所示，每个通道上面的感受野与卷积核对应通道上面的矩阵相乘累加，得到中间变量 10、20、20，全部相加得到输出 50，写入第一行、第二列元素位置。

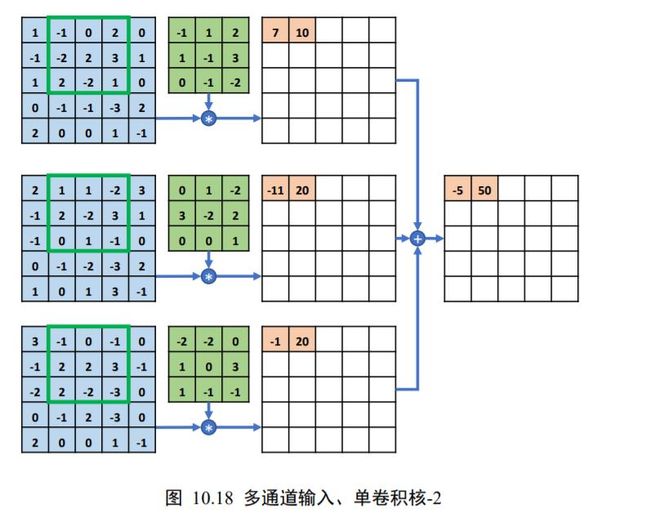
以此方式同步移动感受野窗口，直至最右边、最下方位置，此时全部完成输入和卷积核的卷积运算，得到3 × 3的输出矩阵，如图 10.19 所示。

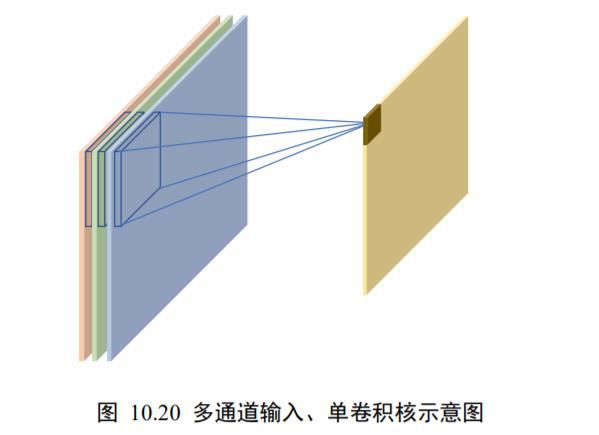
整个的计算示意图如下图 10.20 所示，输入的每个通道处的感受野均与卷积核的对应通道相乘累加，得到与通道数量相等的中间变量，这些中间变量全部相加即得到当前位置的输出值。输入通道的通道数量决定了卷积核的通道数。一个卷积核只能得到一个输出矩阵，无论输入的通道数量。

一般来说，一个卷积核只能完成某种逻辑的特征提取，当需要同时提取多种逻辑特征时，可以通过增加多个卷积核来得到多种特征，提高神经网络的表达能力，这就是多通道输入、多卷积核的情况。

10.2.3 多通道输入、多卷积核

多通道输入、多卷积核是卷积神经网络中最为常见的形式，前面我们已经介绍了单卷积核的运算过程，每个卷积核和输入做卷积运算，得到一个输出矩阵。当出现多卷积核时，第 ( ∈[1, ] ，为卷积核个数)个卷积核与输入运算得到第个输出矩阵(也称为输出张量的通道），最后全部的输出矩阵在通道维度上进行拼接(Stack 操作，创建输出通道数的新维度)，产生输出张量，包含了个通道数。

以 3 通道输入、2 个卷积核的卷积层为例。第一个卷积核与输入运算得到输出的第一个通道，第二个卷积核与输入运算得到输出的第二个通道，如下图 10.21 所示，输出的两个通道拼接在一起形成了最终输出。每个卷积核的大小、步长、填充设定等都是统一设置，这样才能保证输出的每个通道大小一致，从而满足拼接的条件。

10.2.4 步长

在卷积运算中，如何控制感受野布置的密度呢？对于信息密度较大的输入，如物体数量很多的图片，为了尽可能的少漏掉有用信息，在网络设计的时候希望能够较密集地布置感受野窗口；对于信息密度较小的输入，比如全是海洋的图片，可以适量的减少感受野窗口的数量。感受野密度的控制手段一般是通过移动步长(Strides)实现的。

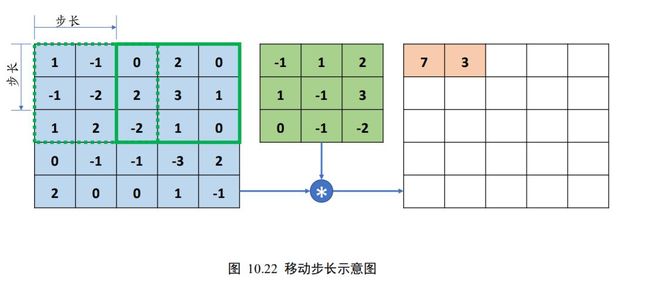
步长是指感受野窗口每次移动的长度单位，对于 2D 输入来说，分为沿(向右)方向和(向下)方向的移动长度。为了简化讨论，这里只考虑/方向移动步长相同的情况，这也是神经网络中最常见的设定。

如下图 10.22 所示，绿色实线代表的感受野窗口的位置是当前位置，绿色虚线代表是上一次感受野所在位置，从上一次位置移动到当前位置的移动长度即是步长的定义。图 10.22 中感受野沿方向的步长为 2，表达为步长 = 2。

当感受野移动至输入右边的边界时，感受野向下移动一个步长 = 2，并回到行首。如下图 10.23 所示，感受野向下移动 2 个单位，并回到行首位置，进行相乘累加运算。

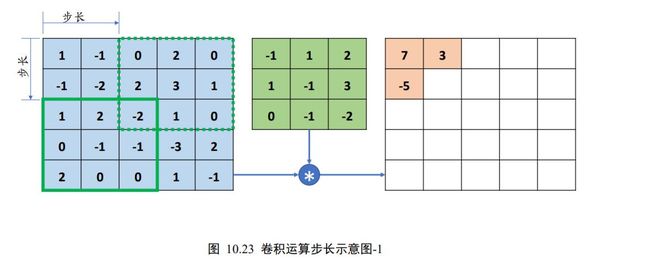
循环往复移动，直至达到最下方、最右边边缘位置，如图 10.24 所示，最终卷积层输出的高宽只有2 × 2。对比前面 =1 的情形，输出高宽由3 × 3降低为2 × 2，感受野的数量减少为仅 4 个。

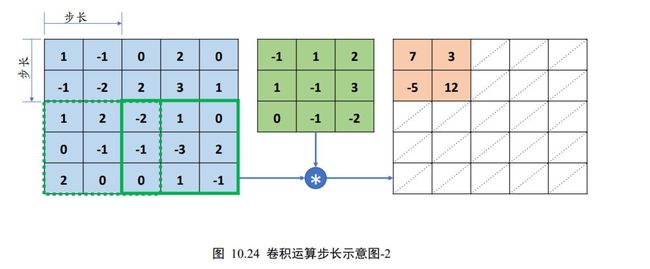
可以看到，通过设定步长，可以有效地控制信息密度的提取。当步长设计的较小时，感受野以较小幅度移动窗口，有利于提取到更多的特征信息，输出张量的尺寸也更大；当步长设计的较大时，感受野以较大幅度移动窗口，有利于减少计算代价，过滤冗余信息，输出张量的尺寸也更小。

10.2.5 填充

经过卷积运算后的输出的高宽一般会小于输入的高宽，即使是步长 =1 时，输出的高宽也会略小于输入高宽。

在网络模型设计时，有时希望输出的高宽能够与输入的高宽相同，从而方便网络参数的设计、残差连接等。

为了让输出的高宽能够与输入的相等，一般通过在原输入的高和宽维度上面进行填充(Padding)若干无效元素操作，得到增大的输入′。通过精心设计填充单元的数量，在′上面进行卷积运算得到输出的高宽可以和原输入相等，甚至更大。

如下图 10.25 所示，在高/行方向的上(Top)、下(Bottom)方向，宽/列方向的左(Left)、右(Right)均可以进行不定数量的填充操作，填充的数值一般默认为 0，也可以填充自定义的数据。图 10.25 中上、下方向各填充 1 行，左、右方向各填充 2 列，得到新的输入′。

那么添加填充后的卷积层怎么运算呢？同样的方法，仅仅是把参与运算的输入从换成了填充后得到的新张量′。如下图 10.26 所示，感受野的初始位置在填充后的′的左上方，完成相乘累加运算，得到输出 1，写入输出张量的对应位置。

移动步长 = 1个单位，重复运算逻辑，得到输出 0，如图 10.27 所示。

循环往复，最终得到 × 的输出张量，如图 10.28 所示。

通过精心设计的 Padding 方案，即上下左右各填充一个单位，记为 =1 ，我们可以得到输出和输入的高、宽相等的结果；在不加 Padding 的情况下，如下图 10.29 所示，只能得到3 × 3的输出，略小于输入。

卷积神经层的输出尺寸$\left[b,h^{\prime },W^{\prime },C_{Out}\right]$由卷积核的数量$C_{out}$，卷积核的大小，步长，填充数(只考虑上下填充数量$p_h$相同，左右填充数量$p_w$相同的情况)以及输入的高宽ℎ/共同决定，它们之间的数学关系可以表达为：
$$h^{\prime }=\lfloor \frac{h+2\cdot p_h-k}{s}\rfloor +1$$
$$w^{\prime }=\lfloor \frac{w+2\cdot p_w-k}{s}\rfloor +1$$
其中$p_h$、$p_w$分别表示高、宽方向的填充数量，⌊∙⌋表示向下取整。以上面的例子为例，ℎ = = 5， = 3，$p_h$=$p_w$=1 ， =1 ，输出的高宽分别为：
$$\begin{array}{l}{h}^{\prime }=\lfloor \frac{5+2\ast 1-3}{1}\rfloor +1=\lfloor 4\rfloor +1=5\\ w^{\prime }=\lfloor \frac{5+2\ast 1-3}{1}\rfloor +1=\lfloor 4\rfloor +1=5\end{array}$$
在 TensorFlow 中，在 =1 时，如果希望输出和输入高、宽相等，只需要简单地设置参数 padding=”SAME”即可使 TensorFlow 自动计算 padding 数量，非常方便。

10.3 卷积层实现

在 TensorFlow 中，既可以通过自定义权值的底层实现方式搭建神经网络，也可以直接调用现成的卷积层类的高层方式快速搭建复杂网络。我们主要以 2D 卷积为例，介绍如何实现卷积神经网络层。

10.3.1 自定义权值

在 TensorFlow 中，通过tf.nn.conv2d函数可以方便地实现 2D 卷积运算。tf.nn.conv2d基于输入: $\left[b,h,w,c_{in}\right]$和卷积核: $\left[k,k,c_{in},c_{out}\right]$进行卷积运算，得到输出 $\left[b,h^{\prime },w^{\prime },c_{out}\right]$，其中$c_{in}$表示输入通道数，$c_{out}$表示卷积核的数量，也是输出特征图的通道数。例如：

x=tf.random.normal([2,5,5,3])#模拟输入，3通道，高宽为5
#需要根据[k,k,cin,cout]格式创建张量W，4个3×3大小卷积核
w=tf.random.normal([3,3,3,4])
#步长为1，padding为0
out=tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[0,0],[0,0],[0,0]])
#输出张量的shape
print(out.shape)

(2, 3, 3, 4)

其中 padding 参数的设置格式为：

padding=[[0,0],[上,下],[左,右],[0,0]]

例如，上下左右各填充一个单位，则 padding 参数设置为 ，实现如下：

x=tf.random.normal([2,5,5,3])#模拟输入，3通道，高宽为5
#需要根据[k,k,cin,cout]格式创建张量W，4个3×3大小卷积核
w=tf.random.normal([3,3,3,4])
#步长为1，padding为0
out=tf.nn.conv2d(x,w,strides=1,padding=[[0,0],[1,1],[1,1],[0,0]])
#输出张量的shape
print(out.shape)

TensorShape([2, 5, 5, 4])

特别地，通过设置参数 padding='SAME'、strides=1可以直接得到输入、输出同大小的卷积层，其中 padding 的具体数量由 TensorFlow 自动计算并完成填充操作。例如：

x=tf.random.normal([2,5,5,3])#模拟输入，3通道，高宽为5
#需要根据[k,k,cin,cout]格式创建张量W，4个3×3大小卷积核
w=tf.random.normal([3,3,3,4])
#步长为，padding设置为输出、输入同大小
# 需要注意的是，padding=same只有在strides=1时才是同大小
out=tf.nn.conv2d(x,w,strides=1,padding='SAME')
#输出张量的shape
print(out.shape)

Out[3]: TensorShape([2, 5, 5, 4])

当 >1 时，设置 padding='SAME'将使得输出高、宽将成$\frac{1}{S}$倍地减少。例如：

x=tf.random.normal([2,5,5,3])#模拟输入，3通道，高宽为5
#需要根据[k,k,cin,cout]格式创建张量W，4个3×3大小卷积核
w=tf.random.normal([3,3,3,4])
# 高宽先padding成可以整除3的最小整数6，然后6按3倍减少，得到2×2
out=tf.nn.conv2d(x,w,strides=3,padding='SAME')
#输出张量的shape
print(out.shape)

TensorShape([2, 2, 2, 4])

卷积神经网络层与全连接层一样，可以设置网络带偏置向量。tf.nn.conv2d 函数是没有实现偏置向量计算的，添加偏置只需要手动累加偏置张量即可。例如：

# 根据[cout]格式创建偏置向量
b = tf.zeros([4])
# 在卷积输出上叠加偏置向量，它会自动 broadcasting 为[b,h',w',cout]
out = out + b
out.shape

TensorShape([2, 2, 2, 4])

10.3.2 卷积层类

通过卷积层类 layers.Conv2D 可以不需要手动定义卷积核和偏置张量，直接调用类实例即可完成卷积层的前向计算，实现更加高层和快捷。

在TensorFlow中，API 的命名有一定的规律，首字母大写的对象一般表示类，全部小写的一般表示函数，如 layers.Conv2D表示卷积层类，nn.conv2d表示卷积运算函数。使用类方式会(在创建类时或 build 时)自动创建需要的权值张量和偏置向量等，用户不需要记忆卷积核张量的定义格式，因此使用起来更简单方便，但是灵活性也略低。

函数方式的接口需要自行定义权值和偏置等，更加灵活和底层。

在新建卷积层类时，只需要指定卷积核数量参数 filters，卷积核大小 kernel_size，步长strides，填充 padding 等即可。如下创建了 4 个3 × 3大小的卷积核的卷积层，步长为 1，padding 方案为’SAME’：

layer = layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')

如果卷积核高宽不等，步长行列方向不等，此时需要将 kernel_size 参数设计为 tuple格式($k_h$, $k_w$)，strides 参数设计为($s_h$ ,$s_w$)。如下创建 4 个3 ×4 大小的卷积核，竖直方向移动步长$s_h$= 2，水平方向移动步长$s_w$=1 ：

layer = layers.Conv2D(4,kernel_size=(3,4),strides=(2,1),padding='SAME')

创建完成后，通过调用实例(的__call__方法)即可完成前向计算，例如：

#创建卷积层类
x=tf.random.normal([2,5,5,3])
layer=layers.Conv2D(4,kernel_size=3,strides=1,padding='SAME')
out=layer(x)#前向计算
print(out.shape)

TensorShape([2, 5, 5, 4])

在类 Conv2D 中，保存了卷积核张量和偏置，可以通过类成员 trainable_variables直接返回和的列表。例如：

# 返回所有待优化张量列表
print(layer.trainable_variables)

[<tf.Variable 'conv2d/kernel:0' shape=(3, 3, 3, 4) dtype=float32, numpy=
array([[[[ 0.13485974, -0.22861657, 0.01000655, 0.11988598],
 [ 0.12811887, 0.20501086, -0.29820845, -0.19579397],
 [ 0.00858489, -0.24469738, -0.08591779, -0.27885547]], …
<tf.Variable 'conv2d/bias:0' shape=(4,) dtype=float32, numpy=array([0., 0.,
0., 0.], dtype=float32)>]

通过调用 layer.trainable_variables 可以返回 Conv2D 类维护的和张量，这个类成员在获取网络层的待优化变量时非常有用。也可以直接调用类实例 layer.kernel、layer.bias名访问和张量。

10.4 LeNet-5 实战

1990 年代，Yann LeCun 等人提出了用于手写数字和机器打印字符图片识别的神经网络，被命名为 LeNet-5。LeNet-5 的提出，使得卷积神经网络在当时能够成功被商用，广泛应用在邮政编码、支票号码识别等任务中。

下图 10.30 是 LeNet-5 的网络结构图，它接受32 × 32大小的数字、字符图片，经过第一个卷积层得到 [b,28,28,6] 形状的张量，经过一个向下采样层，张量尺寸缩小到[b,14,14,6] ，经过第二个卷积层，得到[b,10,10,16]形状的张量，同样经过下采样层，张量尺寸缩小到[b,5,5,16] ，在进入全连接层之前，先将张量打成[b,400] 的张量，送入输出节点数分别为 120、84 的 2 个全连接层，得到[b,84]的张量，最后通过 Gaussian connections 层。

现在看来，LeNet-5 网络层数较少(2 个卷积层和 2 个全连接层)，参数量较少，计算代价较低，尤其在现代 GPU 的加持下，数分钟即可训练好 LeNet-5 网络。

我们在 LeNet-5 的基础上进行了少许调整，使得它更容易在现代深度学习框架上实现。首先我们将输入形状由32 × 32调整为28 × 28，然后将 2 个下采样层实现为最大池化层(降低特征图的高、宽，后续会介绍)，最后利用全连接层替换掉 Gaussian connections层。下文统一称修改的网络也为 LeNet-5 网络。网络结构图如图 10.31 所示。

我们基于 MNIST 手写数字图片数据集训练 LeNet-5 网络，并测试其最终准确度。

import tensorflow as tf
# 导入误差计算，优化器模块
from tensorflow.keras import Sequential, layers, losses, datasets, optimizers

# 获取 GPU 设备列表
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
    try:
        # 设置 GPU 为增长式占用
        for gpu in gpus:
            tf.config.experimental.set_memory_growth(gpu, True)
    except RuntimeError as e:
        # 打印异常
        print(e)

加载数据集以及对数据进行预处理。

def preprocess(x, y):
    # [b, 28, 28], [b]
    print(x.shape, y.shape)
    x = tf.cast(x, dtype=tf.float32) / 255.
    x = tf.reshape(x, [-1, 28, 28])
    y = tf.cast(y, dtype=tf.int64)

    return x, y


def load_dataset():
    (x, y), (x_test, y_test) = datasets.mnist.load_data()

    batchsz = 128
    train_db = tf.data.Dataset.from_tensor_slices((x, y))
    train_db = train_db.shuffle(1000).batch(batchsz).map(preprocess)

    test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
    test_db = test_db.shuffle(1000).batch(batchsz).map(preprocess)

    return train_db, test_db

首先通过 Sequential 容器创建 LeNet-5，代码如下：

from tensorflow.keras import Sequential

network=Sequential([
    layers.Conv2D(6,kernel_size=3,strides=1),#第一个卷积层，6个3*3卷积核
    layers.MaxPooling2D(pool_size=2,strides=2),# 宽和高各减半的池化层
    layers.ReLU(),#激活函数
    layers.Conv2D(16,kernel_size=3,strides=1),#第二个卷积层，16个3*3卷积核
    layers.MaxPooling2D(pool_size=2,strides=2),#宽高各减半的池化层
    layers.ReLU(),#激活函数
    layers.Flatten(),#打平层，方便全连接层处理

    layers.Dense(120,activation='relu'),#全连接层，120个节点
    layers.Dense(84,activation='relu'),#全连接层，84节点
    layers.Dense(10)#全连接层，10个节点
])
#build一次网络模型，给输入X的形状，其中4为随意给的batchsz
network.build(input_shape=(4,28,28,1))
#统计网络信息
print(network.summary())

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (4, 26, 26, 6)            60        
_________________________________________________________________
max_pooling2d (MaxPooling2D) (4, 13, 13, 6)            0         
_________________________________________________________________
re_lu (ReLU)                 (4, 13, 13, 6)            0         
_________________________________________________________________
conv2d_2 (Conv2D)            (4, 11, 11, 16)           880       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (4, 5, 5, 16)             0         
_________________________________________________________________
re_lu_1 (ReLU)               (4, 5, 5, 16)             0         
_________________________________________________________________
flatten (Flatten)            (4, 400)                  0         
_________________________________________________________________
dense_4 (Dense)              (4, 120)                  48120     
_________________________________________________________________
dense_5 (Dense)              (4, 84)                   10164     
_________________________________________________________________
dense_6 (Dense)              (4, 10)                   850       
=================================================================
Total params: 60,074
Trainable params: 60,074
Non-trainable params: 0

通过summary()函数统计出每层的参数量，打印出网络结构信息和每层参数量详情，如表
10.3 所示，我们可以与全连接网络的参数量表 10.1 进行比较。

可以看到，卷积层的参数量非常少，主要的参数量集中在全连接层。由于卷积层将输入特征维度降低很多，从而使得全连接层的参数量不至于过大，整个模型的参数量约 60K，而表 10.1 中的全连接网络参数量达到了 34 万个，因此通过卷积神经网络可以显著降低网络参数量，同时增加网络深度。

在训练阶段，首先将数据集中 shape 为[b,28,28]的输入增加一个维度，调整 shape 为[b,28,28,1]送入模型进行前向计算，得到输出张量 output，shape 为[b,10] 。我们新建交叉熵损失函数类(没错，损失函数也能使用类方式)用于处理分类任务，通过设定from_logits=True 标志位将 softmax 激活函数实现在损失函数中，不需要手动添加损失函数，提升数值计算稳定性。代码如下：

#导入误差计算，优化器模块
from tensorflow.keras import losses,optimizers
#创建损失函数的类，在实际计算时直接调用类实例即可
criteon=losses.CategoricalCrossentropy(from_logits=True)

完整训练过程实现如下：

def train(train_db, network, criteon, optimizer, epoch_num):
    for epoch in range(epoch_num):
        correct, total, loss = 0, 0, 0
        for step, (x, y) in enumerate(train_db):
            # 构建梯度记录环境
            with tf.GradientTape() as tape:
                # 插入通道维度， =>[b,28,28,1]
                x = tf.expand_dims(x, axis=3)
                # 前向计算，获得 10 类别的概率分布， [b, 784] => [b, 10]
                out = network(x)
                pred = tf.argmax(out, axis=-1)
                # 真实标签 one-hot 编码， [b] => [b, 10]
                y_onehot = tf.one_hot(y, depth=10)
                # 计算交叉熵损失函数，标量
                loss += criteon(y_onehot, out)
                # 统计预测正确数量
                correct += float(tf.reduce_sum(tf.cast(tf.equal(pred, y), tf.float32)))
                # 统计预测样本总数
                total += x.shape[0]


            # 自动计算梯度
            grads = tape.gradient(loss, network.trainable_variables)
            # 自动更新参数
            optimizer.apply_gradients(zip(grads, network.trainable_variables))

        print(epoch, 'loss=', float(loss), 'acc=', correct / total)

    return network

获得损失值后，通过 TensorFlow 的梯度记录器 tf.GradientTape()来计算损失函数 loss 对网络参数 network.trainable_variables 之间的梯度，并通过 optimizer 对象自动更新网络权值参数。代码如下：

            # 自动计算梯度
            grads = tape.gradient(loss, network.trainable_variables)
            # 自动更新参数
            optimizer.apply_gradients(zip(grads, network.trainable_variables))

重复上述步骤若干次后即可完成训练工作。

在测试阶段，由于不需要记录梯度信息，代码一般不需要写在 with tf.GradientTape() as tape 环境中。前向计算得到的输出经过 softmax 函数后，代表了网络预测当前图片输入属于类别的概率(标签是|)， ∈[0, 9] 。通过 argmax 函数选取概率最大的元素所在的索引，作为当前的预测类别，与真实标注比较，通过计算比较结果中间 True 的数量并求和来统计预测正确的样本的个数，最后除以总样本的个数，得出网络的测试准确度。代码如下：

def predict(test_db, network):
    # 记录预测正确的数量，总样本数量
    correct, total = 0, 0
    for x, y in test_db:  # 遍历所有训练集样本
        # 插入通道维度， =>[b,28,28,1]
        x = tf.expand_dims(x, axis=3)
        # 前向计算，获得 10 类别的预测分布， [b, 784] => [b, 10]
        out = network(x)
        # 真实的流程时先经过 softmax，再 argmax
        # 但是由于 softmax 不改变元素的大小相对关系，故省去
        pred = tf.argmax(out, axis=-1)
        y = tf.cast(y, tf.int64)
        # 统计预测正确数量
        correct += float(tf.reduce_sum(tf.cast(tf.equal(pred, y), tf.float32)))
        # 统计预测样本总数
        total += x.shape[0]

    # 计算准确率
    print('test acc:', correct / total)

在数据集上面循环训练 30 个 Epoch 后，网络的训练准确度达到了 98.1%，测试准确度也达到了 97.7%。对于非常简单的手写数字图片识别任务，古老的 LeNet-5 网络已经可以取得很好的效果，但是稍复杂一点的任务，比如彩色动物图片识别，LeNet-5 性能就会急剧下降。

接下来，我们总结一下上述所有的知识点。

import tensorflow as tf
# 导入误差计算，优化器模块
from tensorflow.keras import Sequential, layers, losses, datasets, optimizers

# 获取 GPU 设备列表
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
    try:
        # 设置 GPU 为增长式占用
        for gpu in gpus:
            tf.config.experimental.set_memory_growth(gpu, True)
    except RuntimeError as e:
        # 打印异常
        print(e)


def preprocess(x, y):
    # [b, 28, 28], [b]
    print(x.shape, y.shape)
    x = tf.cast(x, dtype=tf.float32) / 255.
    x = tf.reshape(x, [-1, 28, 28])
    y = tf.cast(y, dtype=tf.int64)

    return x, y


def load_dataset():
    (x, y), (x_test, y_test) = datasets.mnist.load_data()

    batchsz = 128
    train_db = tf.data.Dataset.from_tensor_slices((x, y))
    train_db = train_db.shuffle(1000).batch(batchsz).map(preprocess)

    test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
    test_db = test_db.shuffle(1000).batch(batchsz).map(preprocess)

    return train_db, test_db


def build_network():
    network = Sequential([  # 网络容器
        layers.Conv2D(6, kernel_size=3, strides=1),  # 第一个卷积层, 6 个 3x3 卷积核
        layers.MaxPooling2D(pool_size=2, strides=2),  # 高宽各减半的池化层
        layers.ReLU(),  # 激活函数
        layers.Conv2D(16, kernel_size=3, strides=1),  # 第二个卷积层, 16 个 3x3 卷积核
        layers.MaxPooling2D(pool_size=2, strides=2),  # 高宽各减半的池化层
        layers.ReLU(),  # 激活函数
        layers.Flatten(),  # 打平层，方便全连接层处理
        layers.Dense(120, activation='relu'),  # 全连接层， 120 个节点
        layers.Dense(84, activation='relu'),  # 全连接层， 84 节点
        layers.Dense(10)  # 全连接层， 10 个节点
    ])
    # build 一次网络模型，给输入 X 的形状，其中 4 为随意给的 batchsz
    network.build(input_shape=(4, 28, 28, 1))
    # 统计网络信息
    network.summary()
    return network


def train(train_db, network, criteon, optimizer, epoch_num):
    for epoch in range(epoch_num):
        correct, total, loss = 0, 0, 0
        for step, (x, y) in enumerate(train_db):
            # 构建梯度记录环境
            with tf.GradientTape() as tape:
                # 插入通道维度， =>[b,28,28,1]
                x = tf.expand_dims(x, axis=3)
                # 前向计算，获得 10 类别的概率分布， [b, 784] => [b, 10]
                out = network(x)
                pred = tf.argmax(out, axis=-1)
                # 真实标签 one-hot 编码， [b] => [b, 10]
                y_onehot = tf.one_hot(y, depth=10)
                # 计算交叉熵损失函数，标量
                loss += criteon(y_onehot, out)
                # 统计预测正确数量
                correct += float(tf.reduce_sum(tf.cast(tf.equal(pred, y), tf.float32)))
                # 统计预测样本总数
                total += x.shape[0]


            # 自动计算梯度
            grads = tape.gradient(loss, network.trainable_variables)
            # 自动更新参数
            optimizer.apply_gradients(zip(grads, network.trainable_variables))

        print(epoch, 'loss=', float(loss), 'acc=', correct / total)

    return network


def predict(test_db, network):
    # 记录预测正确的数量，总样本数量
    correct, total = 0, 0
    for x, y in test_db:  # 遍历所有训练集样本
        # 插入通道维度， =>[b,28,28,1]
        x = tf.expand_dims(x, axis=3)
        # 前向计算，获得 10 类别的预测分布， [b, 784] => [b, 10]
        out = network(x)
        # 真实的流程时先经过 softmax，再 argmax
        # 但是由于 softmax 不改变元素的大小相对关系，故省去
        pred = tf.argmax(out, axis=-1)
        y = tf.cast(y, tf.int64)
        # 统计预测正确数量
        correct += float(tf.reduce_sum(tf.cast(tf.equal(pred, y), tf.float32)))
        # 统计预测样本总数
        total += x.shape[0]

    # 计算准确率
    print('test acc:', correct / total)


def main():
    epoch_num = 30

    train_db, test_db = load_dataset()
    network = build_network()
    # 创建损失函数的类，在实际计算时直接调用类实例即可
    criteon = losses.CategoricalCrossentropy(from_logits=True)
    optimizer = optimizers.RMSprop(0.001)
    network = train(train_db, network, criteon, optimizer, epoch_num)
    predict(test_db, network)

if __name__ == '__main__':
    main()

输出结果如下，可见训练效果还不错。

(None, 28, 28) (None,)
(None, 28, 28) (None,)
Model: "sequential_4"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_8 (Conv2D)            multiple                  60        
_________________________________________________________________
max_pooling2d_8 (MaxPooling2 multiple                  0         
_________________________________________________________________
re_lu_8 (ReLU)               multiple                  0         
_________________________________________________________________
conv2d_9 (Conv2D)            multiple                  880       
_________________________________________________________________
max_pooling2d_9 (MaxPooling2 multiple                  0         
_________________________________________________________________
re_lu_9 (ReLU)               multiple                  0         
_________________________________________________________________
flatten_4 (Flatten)          multiple                  0         
_________________________________________________________________
dense_12 (Dense)             multiple                  48120     
_________________________________________________________________
dense_13 (Dense)             multiple                  10164     
_________________________________________________________________
dense_14 (Dense)             multiple                  850       
=================================================================
Total params: 60,074
Trainable params: 60,074
Non-trainable params: 0
_________________________________________________________________
0 loss= 135.04367065429688 acc= 0.91455
1 loss= 40.35447692871094 acc= 0.9736333333333334
2 loss= 28.032947540283203 acc= 0.9815166666666667
3 loss= 21.78510093688965 acc= 0.9854833333333334
4 loss= 17.67403221130371 acc= 0.9877666666666667
5 loss= 14.373819351196289 acc= 0.9902333333333333
6 loss= 11.992131233215332 acc= 0.9917166666666667
7 loss= 10.650928497314453 acc= 0.9926333333333334
8 loss= 8.893635749816895 acc= 0.99365
9 loss= 7.410651206970215 acc= 0.9949666666666667
10 loss= 6.5429840087890625 acc= 0.9955
11 loss= 5.767464637756348 acc= 0.9957833333333334
12 loss= 5.1342244148254395 acc= 0.9964833333333334
13 loss= 4.76762056350708 acc= 0.99665
14 loss= 4.071495056152344 acc= 0.9971666666666666
15 loss= 3.3102405071258545 acc= 0.99785
16 loss= 3.527087450027466 acc= 0.9975333333333334
17 loss= 2.926004409790039 acc= 0.99795
18 loss= 2.8832032680511475 acc= 0.99815
19 loss= 2.596499443054199 acc= 0.99825
20 loss= 2.322714328765869 acc= 0.9984166666666666
21 loss= 2.272839069366455 acc= 0.9983833333333333
22 loss= 2.3042337894439697 acc= 0.99825
23 loss= 2.036952018737793 acc= 0.9984666666666666
24 loss= 1.6261500120162964 acc= 0.99885
25 loss= 1.768705129623413 acc= 0.9987833333333334
26 loss= 2.0271694660186768 acc= 0.99875
27 loss= 1.9127095937728882 acc= 0.9985
28 loss= 1.650101900100708 acc= 0.9988833333333333
29 loss= 1.422216534614563 acc= 0.9989666666666667
test acc: 0.9877

10.5 表示学习

我们已经介绍完卷积神经网络层的工作原理与实现方法，复杂的卷积神经网络模型也是基于卷积层的堆叠构成的。

在过去的一段时间内，研究人员发现网络层数越深，模型的表达能力越强，也就越有可能取得更好的性能。那么层层堆叠的卷积网络到底学到了什么特征，使得层数越深，网络的表达能力越强呢？

2014 年，Matthew D. Zeiler 等人尝试利用可视化的方法去理解卷积神经网络到底学到了什么。通过将每层的特征图利用“反卷积”网络(Deconvolutional Network)映射回输入图片，即可查看学到的特征分布，如图 10.32 所示。

可以观察到，第二层的特征对应到边、角、色彩等底层图像提取；第三层开始捕获到纹理这些中层特征；第四、五层呈现了物体的部分特征，如小狗的脸部、鸟类的脚部等高层特征。通过这些可视化的手段，我们可以一定程度上感受卷积神经网络的特征学习过程。


图片数据的识别过程一般认为也是表示学习(Representation Learning)的过程，从接受到的原始像素特征开始，逐渐提取边缘、角点等底层特征，再到纹理等中层特征，再到头部、物体部件等高层特征，最后的网络层基于这些学习到的抽象特征表示(Representation)做分类逻辑的学习。学习到的特征越高层、越准确，就越有利于分类器的分类，从而获得较好的性能。从表示学习的角度来理解，卷积神经网络通过层层堆叠来逐层提取特征，网络训练的过程可以看成特征的学习过程，基于学习到的高层抽象特征可以方便地进行分类任务。

应用表示学习的思想，训练好的卷积神经网络往往能够学习到较好的特征，这种特征的提取方法一般是通用的。比如在猫、狗任务上学习到头、脚、身躯等特征的表示，在其它动物上也能够一定程度上使用。基于这种思想，可以将在任务 A 上训练好的深层神经网络的前面数个特征提取层迁移到任务 B 上，只需要训练任务 B 的分类逻辑(表现为网络的最末数层)，即可取得非常好的效果，这种方式是迁移学习的一种，从神经网络角度也称为网络微调(Fine-tuning)。

10.6 梯度传播

在完成手写数字图片识别实战后，我们对卷积神经网络的使用有了初步的了解。现在我们来解决一个关键问题，卷积层通过移动感受野的方式实现离散卷积操作，那么它的梯度传播是怎么进行的呢？

考虑一简单的情形，输入为3 × 3的单通道矩阵，与一个2 × 2的卷积核，进行卷积运算，输出结果打平后直接与虚构的标注计算误差，如图 10.33 所示。我们来讨论这种情况下的梯度更新方式。

首先推导出输出张量的表达形式：

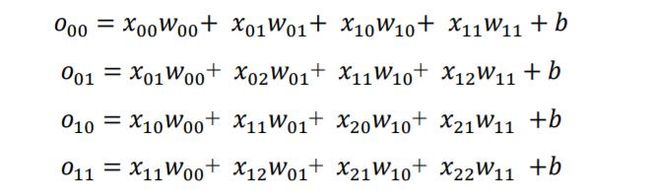
以$W_{00}$的梯度计算为例，通过链式法则分解：
$$\frac{\partial \mathcal{L}}{\partial w_{00}}=\sum _{i\in \{00,01,10,11\}}\frac{\partial \mathcal{L}}{\partial o_i}\frac{\partial o_i}{\partial w_{00}}$$
其中$\frac{\partial \mathcal{L}}{\partial O_i}$可直接由误差函数推导出来，我们直接来考虑$\frac{\partial O_i}{\partial w_i}$，例如：

$$\frac{\partial o_{00}}{\partial w_{00}}=\frac{\partial \left(x_{00}{w}_{00}+x_{01}{w}_{01}+x_{10}{w}_{10}+x_{11}{w}_{11}+b\right)}{w_{00}}=x_{00}$$
同样的方法，可以推导出：

可以观察到，通过循环移动感受野的方式并没有改变网络层可导性，同时梯度的推导也并不复杂，只是当网络层数增大以后，人工梯度推导将变得十分的繁琐。不过不需要担心，深度学习框架可以帮我们自动完成所有参数的梯度计算与更新，我们只需要设计好网络结构即可。

10.7 池化层

在卷积层中，可以通过调节步长参数实现特征图的高宽成倍缩小，从而降低了网络的参数量。实际上，除了通过设置步长，还有一种专门的网络层可以实现尺寸缩减功能，它就是这里要介绍的池化层(Pooling Layer)。

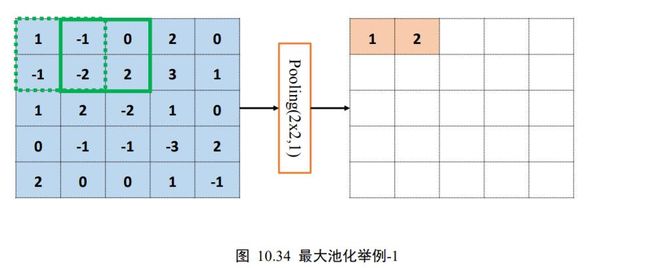
池化层同样基于局部相关性的思想，通过从局部相关的一组元素中进行采样或信息聚合，从而得到新的元素值。特别地，最大池化层(Max Pooling)从局部相关元素集中选取最大的一个元素值，平均池化层(Average Pooling)从局部相关元素集中计算平均值并返回。以 5×5 输入的最大池化层为例，考虑池化感受野窗口大小 = 2，步长 =1 的情况，如下图 10.34 所示。绿色虚线方框代表第一个感受野的位置，感受野元素集合为
$$\{1,-1,-1,-2\}$$
在最大池化采样的方法下，通过
$$x^{\prime }=\max (\{1,-1,-1,-2\})=1$$
计算出当前位置的输出值为 1，并写入对应位置。
若采用的是平均池化操作，则此时的输出值应为
$$x^{\prime }=\mathrm{avg}(\{1,-1,-1,-2\})=-0.75$$
计算完当前位置的感受野后，与卷积层的计算步骤类似，将感受野按着步长向右移动若干单位，此时的输出
$$x^{\prime }=\max (-1,0,-2,2)=2$$
同样的方法，逐渐移动感受野窗口至最右边，计算出输出$x^{\prime }=\max (2,0,3,1)=1$，此时窗口已经到达输入边缘，按照卷积层同样的方式，感受野窗口向下移动一个步长，并回到行首，如图 10.35。

循环往复，直至最下方、最右边，获得最大池化层的输出，长宽为 4×4 ，略小于输入的高宽，如图 10.36。

由于池化层没有需要学习的参数，计算简单，并且可以有效减低特征图的尺寸，非常适合图片这种类型的数据，在计算机视觉相关任务中得到了广泛的应用。

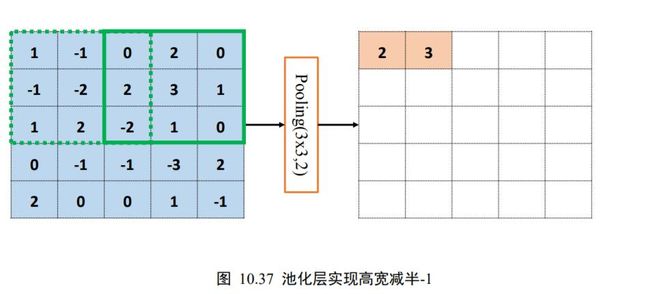
通过精心设计池化层感受野的高宽和步长参数，可以实现各种降维运算。比如，一种常用的池化层设定是感受野大小 = 2，步长 = 2，这样可以实现输出只有输入高宽一半的目的。如下图 10.37、图 10.38 所示，感受野 = 3，步长 = 2，输入高宽为 × ，输出高宽只有2 × 2。

10.8 BatchNorm 层

卷积神经网络的出现，网络参数量大大减低，使得几十层的深层网络成为可能。然而，在残差网络出现之前，网络的加深使得网络训练变得非常不稳定，甚至出现网络长时间不更新甚至不收敛的现象，同时网络对超参数比较敏感，超参数的微量扰动也会导致网络的训练轨迹完全改变。

2015 年，Google 研究人员 Sergey Ioffe 等提出了一种参数标准化(Normalize)的手段，并基于参数标准化设计了 Batch Nomalization(简写为 BatchNorm，或 BN)层。

BN 层的提出，使得网络的超参数的设定更加自由，比如更大的学习率、更随意的网络初始化等，同时网络的收敛速度更快，性能也更好。BN 层提出后便广泛地应用在各种深度网络模型上，卷积层、BN 层、ReLU 层、池化层一度成为网络模型的标配单元块，通过堆叠 ConvBN-ReLU-Pooling 方式往往可以获得不错的模型性能。

首先我们来探索，为什么需要对网络中的数据进行标准化操作？这个问题很难从理论层面解释透彻，即使是 BN 层的作者给出的解释也未必让所有人信服。与其纠结其缘由，不如通过具体问题来感受数据标准化后的好处。

考虑 Sigmoid 激活函数和它的梯度分布，如下图 10.39 所示，Sigmoid 函数在 ∈[−2 ,2] 区间的导数在 [0.1, 0.25]区间分布；当 > 2 或 < −2时，Sigmoid 函数的导数变得很小，逼近于 0，从而容易出现梯度弥散现象。为了避免因为输入较大或者较小而导致Sigmoid 函数出现梯度弥散现象，将函数输入标准化映射到 0 附近的一段较小区间将变得非常重要，可以从图 10.39 看到，通过标准化重映射后，值被映射在 0 附近，此处的导数值不至于过小，从而不容易出现梯度弥散现象。这是使用标准化手段受益的一个例子。

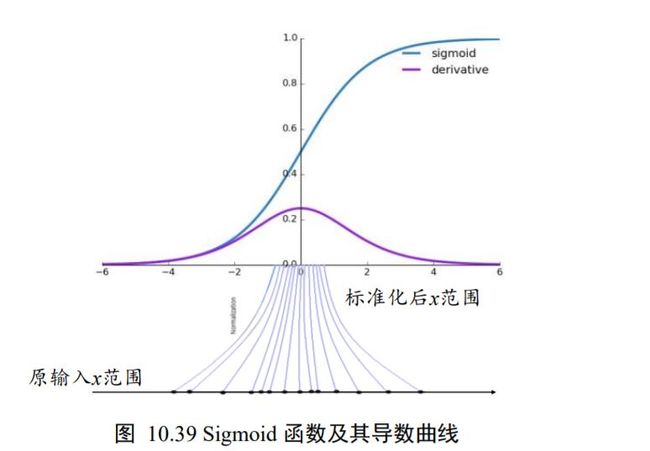
我们再看另一个例子。考虑 2 个输入节点的线性模型，如图 10.40(a)所示：
$$\mathcal{L}=a=x_1{w}_1+x_2{w}_2+b$$
讨论如下 2 种输入分布下的优化问题：
❑ 输入1 ∈[1,10] ，2 ∈[1,10]
❑ 输入1 ∈[1,10] ，2 ∈[100,1000]
由于模型相对简单，可以绘制出 2 种1、2下，函数的损失等高线图，图 10.40(b)是1 ∈
1,10] 、2 ∈[100,1000]时的某条优化轨迹线示意，图 10.40©是1 ∈[1,10] 、2 ∈[1,10]时的某条优化轨迹线示意，图中的圆环中心即为全局极值点。

考虑到

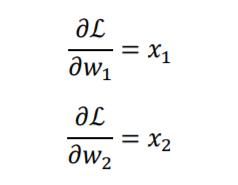
当1、2输入分布相近时，$\frac{\partial \mathcal{L}}{\partial w_1}$、$\frac{\partial \mathcal{L}}{\partial w_2}$偏导数值相当，函数的优化轨迹如图 10.40©所示；
当1、2输入分布差距较大时，比如1 ≪ 2，则
$$\frac{\partial \mathcal{L}}{\partial w_1}\ll \frac{\partial \mathcal{L}}{\partial w_2}$$
损失函数等势线在$w_2$轴更加陡峭，某条可能的优化轨迹如图 10.40(b)所示。对比 2 条优化
线可以观察到，1、2分布相近时图 10.40©中收敛更加快速，优化轨迹更理想。

通过上述的 2 个例子，我们能够经验性归纳出：网络层输入分布相近，并且分布在较小范围内时(如 0 附近)，更有利于函数的优化。那么如何保证输入的分布相近呢？数据标准化可以实现此目的，通过数据标准化操作可以将数据映射到̂:
$$\hat{x}=\frac{x-{\mu }_r}{\sqrt{{\sigma }_r^2+ϵ}}$$
其中${\mu }_r$、2来自统计的所有数据的均值和方差，是为防止出现除 0 错误而设置的较小数字，如 1e − 8。

在基于 Batch 的训练阶段，如何获取每个网络层所有输入的统计数据${\mu }_r$、${\sigma }_r^2$？考虑 Batch 内部的均值${\mu }_B$和方差${\sigma }_B^2$
$${\mu }_B=\frac{1}{m}\sum _{i=1}^m{x}_i$$
$${\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m{\left(x_i-{\mu }_B\right)}^2$$
可以视为近似于${\mu }_r$、${\sigma }_r^2$，其中为 Batch 样本数。因此，在训练阶段，通过
$${\hat{x}}_{\text{train }}=\frac{x_{\text{train }}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}$$
标准化输入，并记录每个 Batch 的统计数据${\mu }_B$和方差${\sigma }_B^2$，用于统计真实的全局${\mu }_r$和方差${\sigma }_r^2$。

在测试阶段，根据记录的每个 Batch 的${\mu }_B$和${\sigma }_B^2$估计出所有训练数据的${\mu }_r$和${\sigma }_r^2$，按着
$${\hat{x}}_{\text{test }}=\frac{x_{\text{test }}-{\mu }_r}{\sqrt{{\sigma }_r^2+ϵ}}$$
将每层的输入标准化。

上述的标准化运算并没有引入额外的待优化变量，${\mu }_r$和${\sigma }_r^2$，${\mu }_B$和${\sigma }_B^2$均由统计得到，不需要参与梯度更新。实际上，为了提高 BN 层的表达能力，BN 层作者引入了“scale and shift”技巧，将̂变量再次映射变换：
$$\tilde{x}=\hat{x}\cdot \gamma +\beta$$

其中参数实现对标准化后的̂再次进行缩放，参数实现对标准化的̂进行平移，不同的是，、参数均由反向传播算法自动优化，实现网络层“按需”缩放平移数据的分布的目的。

下面我们来学习在 TensorFlow 中实现的 BN 层的方法。

10.8.1 前向传播

我们将 BN 层的输入记为，输出记为̃。分训练阶段和测试阶段来讨论前向传播过程。

训练阶段：首先计算当前 Batch 的${\mu }_B$、${\sigma }_B^2$，根据
$${\tilde{x}}_{\text{train }}=\frac{x_{\text{train }}-{\mu }_B}{\sqrt{{\sigma }_B^2+ϵ}}\cdot \gamma +\beta$$
计算 BN 层的输出。

同时按照
$$\begin{array}{c}{\mu }_r\leftarrow \text{ momentum }\cdot {\mu }_r+(1-\text{ momentum })\cdot {\mu }_B\\ {\sigma }_r^2\leftarrow \text{ momentum }\cdot {\sigma }_r^2+(1-\text{ momentum })\cdot {\sigma }_B^2\end{array}$$
迭代更新全局训练数据的统计值${\mu }_r$和${\sigma }_r^2$，其中 momentum 是需要设置一个超参数，用于平衡${\mu }_r$和${\sigma }_r^2$的更新幅度：当momentum =0 时,${\mu }_r$和${\sigma }_r^2$直接被设置为最新一个 Batch 的${\mu }_B$和${\sigma }_B^2$；当momentum =1时,${\mu }_r$和${\sigma }_r^2$保持不变，忽略最新一个 Batch 的${\mu }_B$和${\sigma }_B^2$，在TensorFlow 中，momentum 默认设置为 0.99。

测试阶段：BN 层根据
$${\tilde{x}}_{\text{test }}=\frac{x_{\text{test }}-{\mu }_r}{\sqrt{{\sigma }_r^2+ϵ}}\ast \gamma +\beta$$
计算输出̃，其中${\mu }_r,{\sigma }_r^2,\gamma ,\beta$均来自训练阶段统计或优化的结果,在测试阶段直接使用，并不会更新这些参数。

10.8.2 反向更新

在训练模式下的反向更新阶段，反向传播算法根据损失ℒ求解梯度$\frac{\partial \mathcal{L}}{\partial \gamma }$和$\frac{\partial \mathcal{L}}{\partial \beta }$，并按着梯度更新法则自动优化、参数。

需要注意的是，对于 2D 特征图输入: [b,ℎ, , ]，BN 层并不是计算每个点的${\mu }_B,{\sigma }_B^2$，而是在通道轴上面统计每个通道上面所有数据的${\mu }_B,{\sigma }_B^2$，因此${\mu }_B,{\sigma }_B^2$是每个通道上所有其它维度的均值和方差。以 shape 为 [100,32, 32, 3 ]的输入为例，在通道轴上面的均值计算如下：

# 构造输入
x=tf.random.normal([100,32,32,3])
#将其他维度合并，仅保留通道维度
x=tf.reshape(x,[-1,3])
#计算其他维度的均值
ub=tf.reduce_mean(x,axis=0)
print(ub)

<tf.Tensor: id=62, shape=(3,), dtype=float32, numpy=array([-0.00222636, -
0.00049868, -0.00180082], dtype=float32)>

数据有个通道数，则有个均值产生。

除了在轴上面统计数据${\mu }_B,{\sigma }_B^2$的方式，我们也很容易将其推广至其它维度计算均值的方式，如图 10.41 所示：

❑ Layer Norm：统计每个样本的所有特征的均值和方差
❑ Instance Norm：统计每个样本的每个通道上特征的均值和方差
❑ Group Norm：将通道分成若干组，统计每个样本的通道组内的特征均值和方差

上面提到的 Normalization 方法均由独立的几篇论文提出，并在某些应用上验证了其相当或者优于 BatchNorm 算法的效果。由此可见，深度学习算法研究并非难于上青天，只要多思考、多锻炼算法工程能力，人人都有机会发表创新性成果。

10.8.3 BN 层实现

在 TensorFlow 中，通过 layers.BatchNormalization()类可以非常方便地实现 BN 层：

# 创建 BN 层
layer=layers.BatchNormalization()

与全连接层、卷积层不同，BN 层的训练阶段和测试阶段的行为不同，需要通过设置training 标志位来区分训练模式还是测试模式。

以 LeNet-5 的网络模型为例，在卷积层后添加 BN 层，代码如下：

network=Sequential([
    layers.Conv2D(6,kernel_size=3,strides=1),
    #插入BN层
    layers.BatchNormalization(),
    layers.MaxPooling2D(pool_size=2,strides=2),
    layers.ReLU(),

    layers.Conv2D(16,kernel_size=3,strides=1),
    #插入BN层
    layers.BatchNormalization(),
    layers.MaxPooling2D(pool_size=2,strides=2),
    layers.ReLU(),

    layers.Flatten(),

    layer.Dense(120,activation='relu'),
    #此处也可以插入BN层
    layers.Dense(84,activation='relu'),
    #此处也可以插入BN层
    layers.Dense(10)
])

在训练阶段，需要设置网络的参数 training=True 以区分 BN 层是训练还是测试模型，代码如下：

with tf.GradientTape() as tape:
    # 插入通道维度
    x=tf.expand_dims(x,axis=3)
    # 前向计算，设置计算模式:[b,784]=>[b,10]
    out=network(x,training=True)

在测试阶段，需要设置 training=False，避免 BN 层采用错误的行为，代码如下：

with tf.GradientTape() as tape:
    # 插入通道维度
    x=tf.expand_dims(x,axis=3)
    # 前向计算，设置计算模式:[b,784]=>[b,10]
    out=network(x,training=False)

10.9 经典卷积网络

自 2012 年 AlexNet的提出以来，各种各样的深度卷积神经网络模型相继被提出，其中比较有代表性的有 VGG 系列 ，GoogLeNet 系列，ResNet 系列 ,DenseNet系列等，他们的网络层数整体趋势逐渐增多。

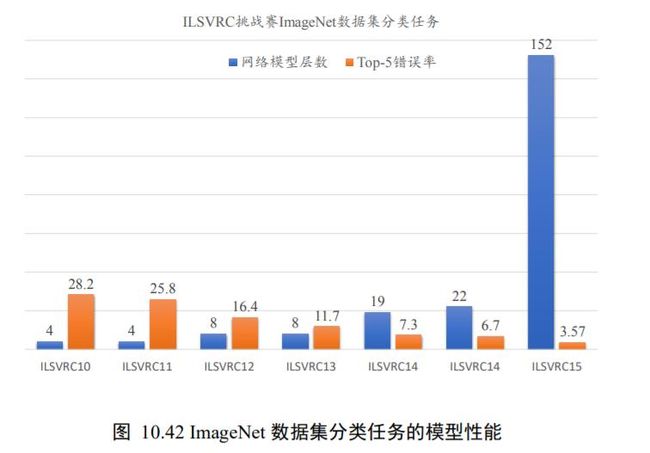
以网络模型在 ILSVRC 挑战赛 ImageNet数据集上面的分类性能表现为例，如图 10.42 所示，在 AlexNet 出现之前的网络模型都是浅层的神经网络，Top-5 错误率均在 25%以上，AlexNet 8 层的深层神经网络将 Top-5 错误率降低至 16.4%，性能提升巨大，后续的 VGG、GoogleNet 模型继续将错误率降低至6.7%；ResNet 的出现首次将网络层数提升至 152 层，错误率也降低至 3.57%。

本节将重点介绍这几种网络模型的特点。

10.9.1 AlexNet

2012 年，ILSVRC12 挑战赛 ImageNet 数据集分类任务的冠军 Alex Krizhevsky 提出了 8层的深度神经网络模型 AlexNet，它接收输入为224 × 224 大小的彩色图片数据，经过五个卷积层和三个全连接层后得到样本属于 1000 个类别的概率分布。
为了降低特征图的维度，AlexNet 在第 1、2、5 个卷积层后添加了 Max Pooling 层，如图 10.43 所示，网络的参数量达到了 6000 万个。为了能够在当时的显卡设备 NVIDIA GTX 580(3GB 显存)上训练模型，Alex Krizhevsky 将卷积层、前 2 个全连接层等拆开在两块显卡上面分别训练，最后一层合并到一张显卡上面，进行反向传播更新。AlexNet 在 ImageNet 取得了 15.3%的 Top-5 错误率，比第二名在错误率上降低了 10.9%。

AlexNet 的创新之处在于：
❑ 层数达到了较深的 8 层。

❑ 采用了 ReLU 激活函数，过去的神经网络大多采用 Sigmoid 激活函数，计算相对复杂，容易出现梯度弥散现象。

❑ 引入 Dropout 层。Dropout 提高了模型的泛化能力，防止过拟合。

10.9.2 VGG 系列

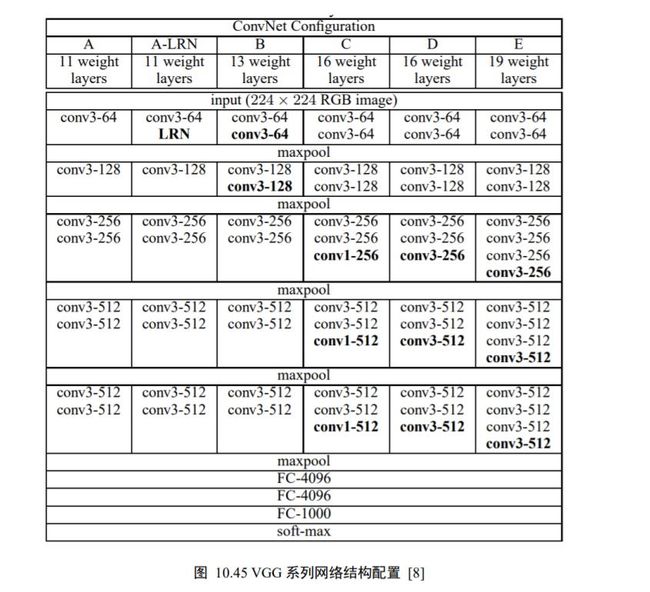
AlexNet 模型的优越性能启发了业界朝着更深层的网络模型方向研究。2014 年，ILSVRC14 挑战赛 ImageNet 分类任务的亚军牛津大学 VGG 实验室提出了 VGG11、VGG13、VGG16、VGG19 等一系列的网络模型(图 10.45)，并将网络深度最高提升至 19层 。

以 VGG16 为例，它接受224 × 224 大小的彩色图片数据，经过 2 个 Conv-ConvPooling 单元，和 3 个 Conv-Conv-Conv-Pooling 单元的叠，最后通过 3 层全连接层输出当前图片分别属于 1000 类别的概率分布，如图 10.44 所示。VGG16 在 ImageNet 取得了7.4%的 Top-5 错误率，比 AlexNet 在错误率上降低了 7.9%。

VGG 系列网络的创新之处在于：
❑ 层数提升至 19 层。

❑ 全部采用更小的3 × 3卷积核，相对于 AlexNet 中 7×7 的卷积核，参数量更少，计算代价更低。

❑ 采用更小的池化层2 × 2窗口和步长 = 2，而 AlexNet 中是步长 = 2、3 × 3的池化窗口。

10.9.3 GoogLeNet

3 × 3的卷积核参数量更少，计算代价更低，同时在性能表现上甚至更优越，因此业界开始探索卷积核最小的情况： 1×1卷积核。如下图 10.46 所示，输入为 3 通道的 5×5 图片，与单个 1×1 的卷积核进行卷积运算，每个通道的数据与对应通道的卷积核运算，得到3 个通道的中间矩阵，对应位置相加得到最终的输出张量。
对于输入 shape 为[b, ℎ, ,$C_{in}$] ，1×1 卷积层的输出为[b, ℎ, ,$C_{out}$] ，其中$C_{in}$为输入数据的通道数，$C_{out}$为输出数据的通道数，也是 1×1 卷积核的数量。 1×1卷积核的一个特别之处在于，它可以不改变特征图的宽高，而只对通道数进行变换。

2014 年，ILSVRC14 挑战赛的冠军 Google 提出了大量采用3 × 3和 1×1 卷积核的网络模型：GoogLeNet，网络层数达到了 22 层。虽然 GoogLeNet 的层数远大于 AlexNet，但是它的参数量却只有 AlexNet 1/12，同时性能也远好于 AlexNet。在 ImageNet 数据集分类任务上，GoogLeNet 取得了 6.7%的 Top-5 错误率，比 VGG16 在错误率上降低了 0.7%。

GoogLeNet 网络采用模块化设计的思想，通过大量堆叠 Inception 模块，形成了复杂的网络结构。如下图 10.47 所示，Inception 模块的输入为，通过 4 个子网络得到 4 个网络输出，在通道轴上面进行拼接合并，形成 Inception 模块的输出。这 4 个子网络是：
❑ 1×1 卷积层。
❑ 1×1 卷积层，再通过一个3 × 3卷积层。
❑ 1×1 卷积层，再通过一个 5×5 卷积层。
❑ 3 × 3最大池化层，再通过 1×1 卷积层。

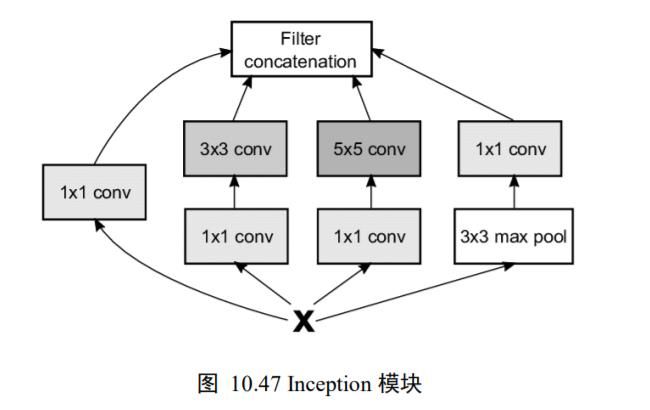
GoogLeNet 的网络结构如图 10.48 所示，其中红色框中的网络结构即为图 10.47的网络结构。

10.10 CIFAR10 与 VGG13 实战

MNIST 是机器学习最常用的数据集之一，但由于手写数字图片非常简单，并且MNIST 数据集只保存了图片灰度信息，并不适合输入设计为 RGB 三通道的网络模型。本节将介绍另一个经典的图片分类数据集：CIFAR10。

CIFAR10 数据集由加拿大 Canadian Institute For Advanced Research 发布，它包含了飞机、汽车、鸟、猫等共 10 大类物体的彩色图片，每个种类收集了 6000 张32 × 32大小图片，共 6 万张图片。其中 5 万张作为训练数据集，1 万张作为测试数据集。每个种类样片如图 10.49 所示。

在TensorFlow中,同样地，不需要手动下载、解析和加载 CIFAR10 数据集，通过datasets.cifar10.load_data()函数就可以直接加载切割好的训练集和测试集。例如：

def preprocess(x, y):
    # [0~1]
    x = 2 * tf.cast(x, dtype=tf.float32) / 255. - 1
    y = tf.cast(y, dtype=tf.int32)
    return x, y


(x,y),(x_test,y_test)=datasets.cifar10.load_data()
#删除y的一个维度，[b,1]=>[b]
y=tf.squeeze(y,axis=1)
y_test=tf.squeeze(y_test,axis=1)
print(x.shape,y.shape,x_test.shape,y_test.shape)
#构建训练集对象，随机打乱，预处理，批量化
train_db=tf.data.Dataset.from_tensor_slices((x,y))
train_db=train_db.shuffle(1000).batch(128).map(preprocess)
#构建测试集对象，预处理，批量化
test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))
test_db=test_db.batch(128).map(preprocess)
# 从训练集中采样一个Batch,并观察
sample=next(iter(train_db))
print('sample:',sample[0].shape,sample[1].shape,tf.reduce_min(sample[0]),tf.reduce_max(sample[0]))

(50000, 32, 32, 3) (50000,) (10000, 32, 32, 3) (10000,)
sample: (128, 32, 32, 3) (128,) tf.Tensor(-1.0, shape=(), dtype=float32) tf.Tensor(1.0, shape=(), dtype=float32)

TensorFlow 会自动将数据集下载在 C:\Users\用户名.keras\datasets 路径下，用户可以查看，也可手动删除不需要的数据集缓存。上述代码运行后，得到训练集的和形状为：(50000, 32, 32, 3)和(50000)，测试集的和形状为(10000, 32, 32, 3)和(10000)，分别代表了图片大小为32 × 32，彩色图片，训练集样本数为 50000，测试集样本数为 10000。

CIFAR10 图片识别任务并不简单，这主要是由于 CIFAR10 的图片内容需要大量细节才能呈现，而保存的图片分辨率仅有32 × 32，使得部分主体信息较为模糊，甚至人眼都很难分辨。浅层的神经网络表达能力有限，很难训练优化到较好的性能，本节将基于表达能力更强的 VGG13 网络，根据我们的数据集特点修改部分网络结构，完成 CIFAR10 图片识别。修改如下：

❑ 将网络输入调整为32 × 32。原网络输入为224 × 224 ，导致全连接层输入特征维度过大，网络参数量过大。
❑ 3 个全连接层的维度调整为 [256,64,10] ，满足 10 分类任务的设定。

图 10.50 是调整后的 VGG13 网络结构，我们统称之为 VGG13 网络模型。

我们将网络实现为 2 个子网络：卷积子网络和全连接子网络。卷积子网络由 5 个子模块构成，每个子模块包含了 Conv-Conv-MaxPooling 单元结构，代码如下：

# 先创建包含多网络层的列表
conv_layers=[
    #Conv-Conv-Pooling单元1
    #64个3*3卷积核，输入输出同大小
    layers.Conv2D(64,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(64,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    #高宽减半
    layers.Maxpool2D(pool_size=[2,2],strides=2,padding='same'),

    #Conv-Conv-Pooling单元2,输出通道提升至128，高宽大小减半
    layers.Conv2D(128,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    layers.Conv2D(128,kernel_size=[3,3],padding='same',activation=tf.nn.relu),
    #高宽减半
    layers.Maxpool2D(pool_size=[2,2],strides=2,padding='same'),

    # Conv-Conv-Pooling单元3,输出通道提升至256，高宽大小减半
    layers.Conv2D(256, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    layers.Conv2D(256, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    # 高宽减半
    layers.Maxpool2D(pool_size=[2, 2], strides=2, padding='same'),

    # Conv-Conv-Pooling单元4,输出通道提升至512，高宽大小减半
    layers.Conv2D(512, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    layers.Conv2D(512, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    # 高宽减半
    layers.Maxpool2D(pool_size=[2, 2], strides=2, padding='same'),

    # Conv-Conv-Pooling单元5，,输出通道提升至512，高宽大小减半
    layers.Conv2D(512, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    layers.Conv2D(512, kernel_size=[3, 3], padding='same', activation=tf.nn.relu),
    # 高宽减半
    layers.Maxpool2D(pool_size=[2, 2], strides=2, padding='same'),
]

# 利用前面创建的层列表构建网络容器
conv_net=Sequential(conv_layers)

全连接子网络包含了 3 个全连接层，每层添加 ReLU 非线性激活函数，最后一层除外。代码如下：

# 创建 3 层全连接层子网络
#创建3层全连接层子网络
fc_net=Sequential([
    layers.Dense(256,activation=tf.nn.relu),
    layers.Dense(128,activation='relu'),
    layers.Dense(10,activation=None),
])

子网络创建完成后，通过如下代码查看网络的参数量：

# build2 个子网络，并打印网络参数信息
conv_net.build(input_shape=[4, 32, 32, 3])
10.11 卷积层变种 41
fc_net.build(input_shape=[4, 512])
conv_net.summary()
fc_net.summary()

卷积网络总参数量约为 940 万个，全连接网络总参数量约为 17.7 万个，网络总参数量约为950 万个，相比于原始版本的 VGG13 参数量减少了很多。

由于我们将网络实现为 2 个子网络，在进行梯度更新时，需要合并 2 个子网络的待优化参数列表。代码如下：

#列表合并，合并2个子网络的参数
variables=conv_net.trainable_varibales+fc_net.trainable_varibales
# 对所有参数求梯度
grads=tape.gradient(loss,variables)
#自动更新
optimizer.apply_gradients(zip(grads,varibales))

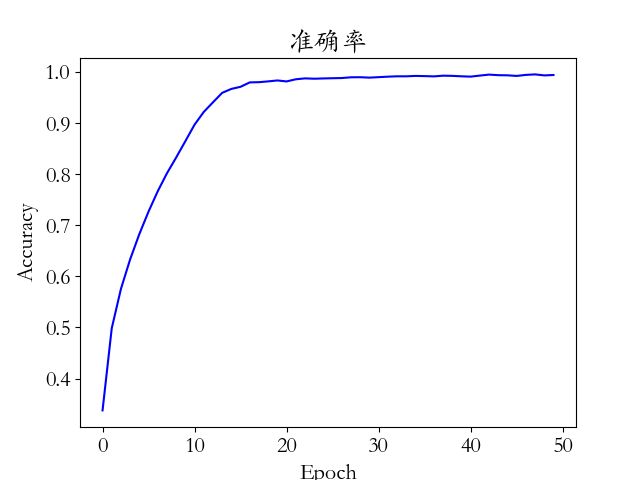
运行 cifar10_train.py 文件即可开始训练模型，在训练完 50 个 Epoch 后，网络的测试准确率达到了 77.5%。

下面我们就用代码总结以下上述知识点。

import os
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import layers,optimizers,datasets,Sequential

plt.rcParams['font.size'] = 16
plt.rcParams['font.family'] = ['STKaiti']
plt.rcParams['axes.unicode_minus'] = False

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
tf.random.set_seed(2345)

os.environ['TF_ENABLE_GPU_GARBAGE_COLLECTION'] = 'false'

# 获取 GPU 设备列表
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
    try:
        # 设置 GPU 为增长式占用
        for gpu in gpus:
            tf.config.experimental.set_memory_growth(gpu, True)
    except RuntimeError as e:
        # 打印异常
        print(e)


def preprocess(x, y):
    # [0~1]
    x = 2 * tf.cast(x, dtype=tf.float32) / 255. - 1
    y = tf.cast(y, dtype=tf.int32)
    return x, y

def load_dataset():
    # 在线下载，加载CIFAR10数据集
    (x,y),(x_test,y_test)=datasets.cifar10.load_data()
    # 删除y的一个维度，[b,1]=>[b]
    y=tf.squeeze(y,axis=1)
    y_test=tf.squeeze(y_test,axis=1)
    # 打印训练集和测试集的形状
    print(x.shape,y.shape,x_test.shape,y_test.shape)
    #构建训练集对象，随机打乱，预处理，批量化
    train_db=tf.data.Dataset.from_tensor_slices((x,y))
    train_db=train_db.shuffle(1000).map(preprocess).batch(128)
    # 构建测试集对象，随机打乱，预处理，批量化
    test_db=tf.data.Dataset.from_tensor_slices((x_test,y_test))
    test_db=test_db.map(preprocess).batch(64)
    # 从训练集中采样一个Batch,并观察
    sample=next(iter(train_db))
    print('sample:', sample[0].shape, sample[1].shape, tf.reduce_min(sample[0]), tf.reduce_max(sample[0]))
    return train_db, test_db

def build_network():
    # 先创建包含多网络层的列表
    conv_layers=[
        # 5 units of conv + max pooling
        # Conv-Conv-Pooling 单元 1
        # 64 个 3x3 卷积核, 输入输出同大小
        layers.Conv2D(64, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.Conv2D(64, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        # 高宽减半
        layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

        # Conv-Conv-Pooling 单元 2,输出通道提升至 128，高宽大小减半
        layers.Conv2D(128, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.Conv2D(128, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

        # Conv-Conv-Pooling 单元 3,输出通道提升至 256，高宽大小减半
        layers.Conv2D(256, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.Conv2D(256, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

        # Conv-Conv-Pooling 单元 4,输出通道提升至 512，高宽大小减半
        layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same'),

        # Conv-Conv-Pooling 单元 5,输出通道提升至 512，高宽大小减半
        layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.Conv2D(512, kernel_size=[3, 3], padding="same", activation=tf.nn.relu),
        layers.MaxPool2D(pool_size=[2, 2], strides=2, padding='same')
    ]

    # 利用前面创建的层列表构建网络容器
    conv_net=Sequential(conv_layers)

    # 创建3层全连接层子网络
    fc_net = Sequential([
        layers.Dense(256, activation=tf.nn.relu),
        layers.Dense(128, activation=tf.nn.relu),
        layers.Dense(10, activation=None),
    ])

    # build 2个子网络，并打印网络参数信息
    conv_net.build(input_shape=[None,32,32,3])
    fc_net.build(input_shape=(None,512))
    conv_net.summary()
    fc_net.summary()

    return conv_net,fc_net

def train(conv_net,fc_net,train_db,optimizer,varibales,epoch):
    for step,(x,y) in enumerate(train_db):
        with tf.GradientTape() as tape:
            #[b,32,32,3]=>[b,1,1,512]
            out=conv_net(x)
            # flatten,=>[b,512]
            out=tf.reshape(out,[-1,512])
            #[b,512]=>[b,10]
            logits=fc_net(out)
            #[b]=>[b,10]
            y_onehot=tf.one_hot(y,depth=10)
            # comput loss
            loss=tf.losses.categorical_crossentropy(y_onehot,logits,from_logits=True)
            loss=tf.reduce_sum(loss)

        # 对所有参数求梯度
        grads=tape.gradient(loss,varibales)
        #自动更新
        optimizer.apply_gradients(zip(grads,varibales))

        if step %100==0:
            print(epoch,step,'loss:',float(loss))

    return conv_net,fc_net

def predict(conv_net,fc_net,test_db,epoch):
    total_num=0
    total_correct=0
    for x,y in test_db:
        out=conv_net(x)
        out=tf.reshape(out,[-1,512])
        logits=fc_net(out)
        prob=tf.nn.softmax(logits,axis=1)
        pred=tf.argmax(prob,axis=1)
        pred=tf.cast(pred,dtype=tf.int32)

        correct=tf.cast(tf.equal(pred,y),dtype=tf.int32)
        correct=tf.reduce_sum(correct)

        total_num+=x.shape[0]
        total_correct+=int(correct)

    acc=total_correct/total_num
    print(epoch,'axx:',acc)
    return acc
def main():
    epoch_num=50

    train_db,test_db=load_dataset()
    conv_net,fc_net=build_network()
    optimizer=optimizers.Adam(lr=1e-4)

    #列表合并，合并2个子网络的参数
    variables=conv_net.trainable_variables+fc_net.trainable_variables

    accs=[]
    for epoch in range(epoch_num):
        conv_net,fc_net=train(conv_net,fc_net,train_db,optimizer,variables,epoch)
        acc=predict(conv_net,fc_net,test_db,epoch)
        accs.append(acc)
    
    x=range(epoch_num)
    plt.title('准确率')
    plt.plot(x,accs,color='blue')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    
    #plt.savefig('cifar10-vgg13-accuracy.png')
    
if __name__=='__main__':
    main() 

10.11 卷积层变种

卷积神经网络的研究产生了各种各样优秀的网络模型，还提出了各种卷积层的变种，本节将重点介绍数种典型的卷积层变种。

10.11.1 空洞卷积

普通的卷积层为了减少网络的参数量，卷积核的设计通常选择较小的 1×1 和3 × 3感受野大小。小卷积核使得网络提取特征时的感受野区域有限，但是增大感受野的区域又会增加网络的参数量和计算代价，因此需要权衡设计。

空洞卷积(Dilated/Atrous Convolution)的提出较好地解决这个问题，空洞卷积在普通卷积的感受野上增加一个 Dilation Rate 参数，用于控制感受野区域的采样步长，如下图10.51 所示：当感受野的采样步长 Dilation Rate 为 1 时，每个感受野采样点之间的距离为1，此时的空洞卷积退化为普通的卷积；当 Dilation Rate 为 2 时，感受野每 2 个单元采样一个点，如图 10.51 中间的绿色方框中绿色格子所示，每个采样格子之间的距离为 2；同样的方法，图 10.51 右边的 Dilation Rate 为 3，采样步长为 3。尽管 Dilation Rate 的增大会使得感受野区域增大，但是实际参与运算的点数仍然保持不变。

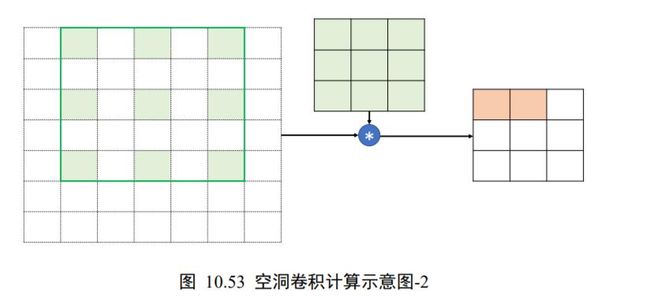
以输入为单通道的 7×7 张量，单个3 × 3卷积核为例，如下图 10.52 所示。在初始位置，感受野从最上、最右位置开始采样，每隔一个点采样一次，共采集 9 个数据点，如图10.52 中绿色方框所示。这 9 个数据点与卷积核相乘运算，写入输出张量的对应位置。

卷积核窗口按着步长为 =1 向右移动一个单位，如图 10.53 所示，同样进行隔点采样，共采样 9 个数据点，与卷积核完成相乘累加运算，写入输出张量对应位置，直至卷积核移动至最下方、最右边位置。需要注意区分的是，卷积核窗口的移动步长和感受野区域的采样步长 Dilation Rate 是不同的概念。

空洞卷积在不增加网络参数的条件下，提供了更大的感受野窗口。但是在使用空洞卷积设置网络模型时，需要精心设计 Dilation Rate 参数来避免出现网格效应，同时较大的Dilation Rate 参数并不利于小物体的检测、语义分割等任务。

在 TensorFlow 中，可以通过设置 layers.Conv2D()类的 dilation_rate 参数来选择使用普通卷积还是空洞卷积。例如：

x = tf.random.normal([1,7,7,1]) # 模拟输入
# 空洞卷积，1 个 3x3 的卷积核
layer = layers.Conv2D(1,kernel_size=3,strides=1,dilation_rate=2)
out = layer(x) # 前向计算
out.shape

TensorShape([1, 3, 3, 1])

当 dilation_rate 参数设置为默认值 1 时，使用普通卷积方式进行运算；当 dilation_rate参数大于 1 时，采样空洞卷积方式进行计算。

10.11.2 转置卷积

转置卷积(Transposed Convolution，或 Fractionally Strided Convolution，部分资料也称之为反卷积/Deconvolution，实际上反卷积在数学上定义为卷积的逆过程，但转置卷积并不能恢复出原卷积的输入，因此称为反卷积并不妥当)通过在输入之间填充大量的 padding 来实现输出高宽大于输入高宽的效果，从而实现向上采样的目的，如图 10.54 所示。我们先介绍转置卷积的计算过程，再介绍转置卷积与普通卷积的联系。

为了简化讨论，我们此处只讨论输入ℎ = ，即输入高宽相等的情况。

+ − 为倍数

考虑输入为2 × 2的单通道特征图，转置卷积核为3 × 3大小，步长 = 2，填充 =0的例子。首先在输入数据点之间均匀插入 −1 个空白数据点，得到3 × 3的矩阵，如图 10.55第 2 个矩阵所示，根据填充量在3 × 3矩阵周围填充相应 − −1 = 3 − 0−1 = 2行/列，此时输入张量的高宽为 7×7 ，如图 10.55 中第 3 个矩阵所示。

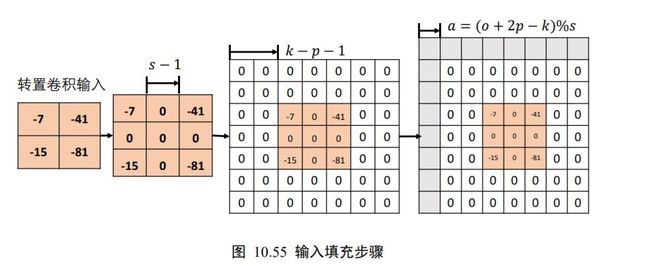
在 7×7 的输入张量上，进行3 × 3卷积核，步长′ =1 ，填充 =0 的普通卷积运算(注意，此阶段的普通卷积的步长′始终为 1，与转置卷积的步长不同)，根据普通卷积的输出计算公式，得到输出大小为：
$$o=|\frac{i+2\ast p-k}{s^{\prime }}\rfloor +1=\lfloor \frac{7+2\ast 0-3}{1}\rfloor +1=5$$
5×5 大小的输出。我们直接按照此计算流程给出最终转置卷积输出与输入关系。在 +
2 − 为 s 倍数时，满足关系
$$o=(i-1)s+k-2p$$
转置卷积并不是普通卷积的逆过程，但是二者之间有一定的联系，同时转置卷积也是基于普通卷积实现的。在相同的设定下，输入经过普通卷积运算后得到 = Conv()，我们将送入转置卷积运算后，得到′ = ConvTranspose()，其中′ ≠ ，但是′与形状相同。我们可以用输入为 5×5 ，步长 = 2，填充 =0 ，3 × 3卷积核的普通卷积运算进行验证演示，如下图 10.56 所示。

可以看到，将转置卷积的输出 5×5 在同设定条件下送入普通卷积，可以得到2 × 2的输出，此大小恰好就是转置卷积的输入大小，同时我们也观察到，输出的2 × 2矩阵并不是转置卷积输入的2 × 2矩阵。转置卷积与普通卷积并不是互为逆过程，不能恢复出对方的输入内容，仅能恢复出等大小的张量。因此称之为反卷积并不贴切。

基于 TensorFlow 实现上述例子的转置卷积运算，代码如下：

#创建X矩阵，高宽各为5*5
x=tf.range(25)+1
# reshape成合法维度的张量
x=tf.reshape(x,[1,5,5,1])
x=tf.cast(x,tf.float32)
# 创建固定内容的卷积核矩阵
w=tf.constant([[-1,2,-3.],[4,-5,6],[-7,8,-9]])
# 调整为合法维度的张量
w=tf.expand_dims(w,axis=2)
w=tf.expand_dims(w,axis=3)
# 进行普通卷积运算
out=tf.nn.conv2d(x,w,strides=2,padding='VALID')
print(out)

<tf.Tensor: id=14, shape=(1, 2, 2, 1), dtype=float32, numpy=
array([[[[ -67.],
 [ -77.]],
 [[-117.],
 [-127.]]]], dtype=float32)>

现在我们将普通卷积的输出作为转置卷积的输入，验证转置卷积的输出是否为 5×5 ，代码如下:

# 普通卷积的输出作为转置卷积的输入，进行转置卷积运算
xx = tf.nn.conv2d_transpose(out, w, strides=2,padding='VALID',output_shape=[1,5,5,1])
# 输出的高宽为 5x5

<tf.Tensor: id=117, shape=(5, 5), dtype=float32, numpy=
array([[ 67., -134., 278., -154., 231.],
[ -268., 335., -710., 385., -462.],
[ 586., -770., 1620., -870., 1074.],
[ -468., 585., -1210., 635., -762.],
[ 819., -936., 1942., -1016., 1143.]], dtype=float32)>

可以看到，转置卷积能够恢复出同大小的普通卷积的输入，但转置卷积的输出并不等同于普通卷积的输入。

+ − 不为倍数

让我们更加深入地分析卷积运算中输入与输出大小关系的一个细节。考虑卷积运算的输出表达式：
$$o=\lfloor \frac{i+2\ast p-k}{s}\rfloor +1$$
当步长s > 时,$\lfloor \frac{i+2\ast p-k}{s}\rfloor$向下取整运算使得出现多种不同输入尺寸对应到相同的输出尺寸上。举个例子，考虑输入大小为 6×6 ，卷积核大小为3 × 3，步长为1的卷积运算，代码如下：

x=tf.random.normal([1,6,6,1])
# 6*6的输入经过普通卷积
out=tf.nn.conv2d(x,w,strides=2,padding='VALID')
print(out)

<tf.Tensor: id=21, shape=(1, 2, 2, 1), dtype=float32, numpy=
array([[[[ 20.438847 ],
[ 19.160788 ]],
[[ 0.8098897],
[-28.30303 ]]]], dtype=float32)>

此种情况也能获得2 × 2大小的卷积输出，与图 10.56 中可以获得相同大小的输出。因此，不同输入大小的卷积运算可能获得相同大小的输出。考虑到卷积与转置卷积输入输出大小关系互换，从转置卷积的角度来说，输入尺寸经过转置卷积运算后，可能获得不同的输出大小。因此通过在图 10.55 中填充行、列来实现不同大小的输出，从而恢复普通卷积不同大小的输入的情况，其中关系为：
$$a=(o+2p-k)\%s$$
此时转置卷积的输出变为：
$$o=(i-1)s+k-2p+a$$
在 TensorFlow 中间，不需要手动指定参数，只需要指定输出尺寸即可，TensorFlow会自动推导需要填充的行列数，前提是输出尺寸合法。例如：

xx=tf.nn.conv2d_transpose(out,w,strides=2,padding='VALID',output_shape=[1,6,6,1])
print(xx)

<tf.Tensor: id=23, shape=(1, 6, 6, 1), dtype=float32, numpy=
array([[[[ -20.438847 ],
[ 40.877693 ],
[ -80.477325 ],
[ 38.321575 ],
[ -57.48236 ],
[ 0. ]],...

通过改变参数 output_shape=[1,5,5,1]也可以获得高宽为 × 的张量。

矩阵角度

转置卷积的转置是指卷积核矩阵产生的稀疏矩阵′在计算过程中需要先转置$w^{\prime T}$，再进行矩阵相乘运算，而普通卷积并没有转置′的步骤。这也是它被称为转置卷积的名字由来。

考虑普通 Conv2d 运算：和，需要根据 strides 将卷积核在行、列方向循环移动获取参与运算的感受野的数据，串行计算每个窗口处的“相乘累加”值，计算效率极低。为了加速运算，在数学上可以将卷积核根据 strides 重排成稀疏矩阵′，再通过′@′一次完成运算(实际上，′矩阵过于稀疏，导致很多无用的 0 乘运算，很多深度学习框架也不是通过这种方式实现的)。

以 4 行 4 列的输入，高宽为3 × 3，步长为 1，无 padding 的卷积核的卷积运算为例，首先将打平成′，如图 10.57 所示。

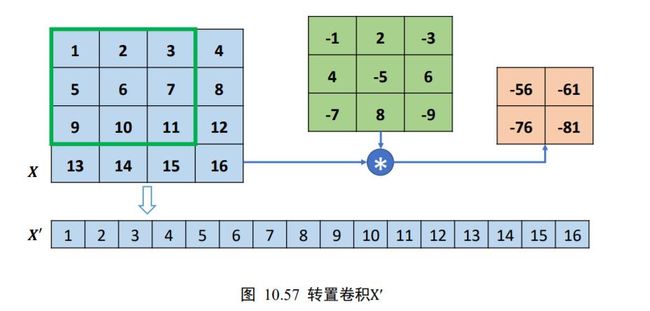
然后将卷积核转换成稀疏矩阵′，如图 10.58 所示。

此时通过一次矩阵相乘即可实现普通卷积运算：
$${\mathbf{O}}^{\prime }={\mathbf{W}}^{\prime }@{\mathbf{X}}^{\prime }$$
如果给定，希望能够生成与同形状大小的张量，怎么实现呢？将′转置后与图 10.57
方法重排后的′完成矩阵相乘即可：
$${\mathbf{X}}^{\prime }={\mathbf{W}}^{\prime \mathrm{T}}@{\mathbf{O}}^{\prime }$$
得到的′通过 Reshape 操作变为与原来的输入尺寸一致，但是内容不同。例如′的 shape为[4,1] ，′T的 shape 为[16,4] ，矩阵相乘得到′的 shape 为[16,1]，Reshape 后即可产生[4,4] 形状的张量。由于转置卷积在矩阵运算时，需要将′转置后才能与转置卷积的输入′矩阵相乘，故称为转置卷积。

转置卷积具有“放大特征图”的功能，在生成对抗网络、语义分割等中得到了广泛应用，如 DCGAN 中的生成器通过堆叠转置卷积层实现逐层“放大”特征图，最后获得十分逼真的生成图片。

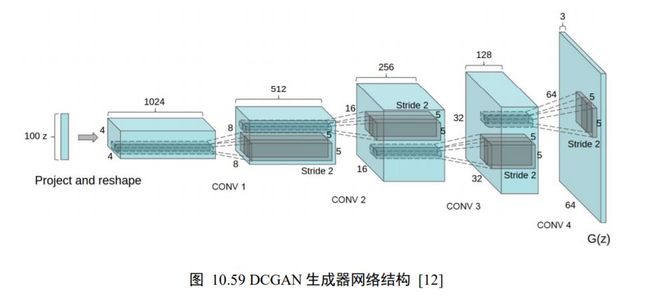
转置卷积实现

在 TensorFlow 中，可以通过 nn.conv2d_transpose 实现转置卷积运算。我们先通过nn.conv2d 完成普通卷积运算。注意转置卷积的卷积核的定义格式为 [ , ,$c_{out}$,$c_{in}$ ]。例如：

#创建4*4大小的输入
x=tf.range(16)+1
x=tf.reshape(x,[1,4,4,1])
#x=tf.cast(x,tf.float32)
#创建3*3卷积核
w=tf.constant([[-1,2,-3],[4,-5,6],[-7,8,-9]])
w=tf.expand_dims(w,axis=2)
w=tf.expand_dims(w,axis=3)
# 普通卷积运算
out=tf.nn.conv2d(x,w,strides=1,padding='VALID')
print(out)

<tf.Tensor: id=42, shape=(1,2,2,1), dtype=float32, numpy=
array([[-56., -61.],
 [-76., -81.]], dtype=float32)>

在保持 strides=1，padding=’VALID’，卷积核不变的情况下，我们通过卷积核 w 与输出 out 的转置卷积运算尝试恢复与输入 x 相同大小的高宽张量，代码如下：

xx=tf.nn.conv2d_transpose(out,w,strides=1,padding='VALID',output_shape=[1,4,4,1])
xx=tf.squeeze(xx)
print(xx)

<tf.Tensor: id=44, shape=(4, 4), dtype=float32, numpy=
array([[ 56., -51., 46., 183.],
 [-148., -35., 35., -123.],
 [ 88., 35., -35., 63.],
 [ 532., -41., 36., 729.]], dtype=float32)>

可以看到，转置卷积生成了 × 的特征图，但特征图的数据与输入 x 并不相同。

在使用 tf.nn.conv2d_transpose 进行转置卷积运算时，需要额外手动设置输出的高宽。tf.nn.conv2d_transpose 并不支持自定义 padding 设置，只能设置为 VALID 或者 SAME。

当设置 padding=’VALID’时，输出大小表达为：
$$o=(i-1)s+k$$
当设置 padding=’SAME’时，输出大小表达为：
$$o=i\cdot s$$
如果读者对转置卷积的原理细节暂时无法理解，可以牢记上述两个表达式即可。例如，2 × 2的转置卷积输入与3 × 3的卷积核运算，strides=1，padding=’VALID’时，输出大小为：
$$h^{\prime }=w^{\prime }=(2-1)\cdot 1+3=4$$
2 × 2的转置卷积输入与3 × 3的卷积核运算，strides=3，padding=’SAME’时，输出大小为：
$$h^{\prime }=w^{\prime }=2\cdot 3=6$$
转置卷积也可以和其他层一样，通过 layers.Conv2DTranspose 类创建一个转置卷积层，然后调用实例即可完成前向计算：

# 创建转置卷积类
layer = layers.Conv2DTranspose(1,kernel_size=3,strides=1,padding='VALID')
xx2 = layer(out) # 通过转置卷积层
xx2

<tf.Tensor: id=130, shape=(1, 4, 4, 1), dtype=float32, numpy=
array([[[[ 9.7032385 ],
[ 5.485071 ],
[ -1.6490463 ],
[ 1.6279562 ]],...

10.11.3 分离卷积

这里以深度可分离卷积(Depth-wise Separable Convolution)为例。普通卷积在对多通道输入进行运算时，卷积核的每个通道与输入的每个通道分别进行卷积运算，得到多通道的特征图，再对应元素相加产生单个卷积核的最终输出，如图 10.60 所示。

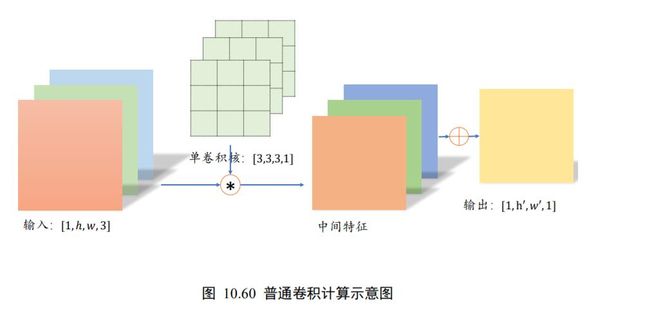
分离卷积的计算流程则不同，卷积核的每个通道与输入的每个通道进行卷积运算，得到多个通道的中间特征，如图 10.61 所示。这个多通道的中间特征张量接下来进行多个 1×1 卷积核的普通卷积运算，得到多个高宽不变的输出，这些输出在通道轴上面进行拼接，从而产生最终的分离卷积层的输出。可以看到，分离卷积层包含了两步卷积运算，第一步卷积运算是单个卷积核，第二个卷积运算包含了多个卷积核。

那么采用分离卷积有什么优势呢？一个很明显的优势在于，同样的输入和输出，采用Separable Convolution的参数量约是普通卷积的1/3。考虑上图中的普通卷积和分离卷积的例
子。普通卷积的参数量是
$$3\cdot 3\cdot 3\cdot 4=108$$
分离卷积的第一部分参数量是
$$3\cdot 3\cdot 3\cdot 1=27$$
第二部分参数量是
$$1\cdot 1\cdot 3\cdot 4=14$$
分离卷积的总参数量只有39，但是却能实现普通卷积同样的输入输出尺寸变换。分离卷积在 Xception 和 MobileNets 等对计算代价敏感的领域中得到了大量应用。

10.12 深度残差网络

AlexNet、VGG、GoogLeNet 等网络模型的出现将神经网络的发展带入了几十层的阶段，研究人员发现网络的层数越深，越有可能获得更好的泛化能力。但是当模型加深以后，网络变得越来越难训练，这主要是由于梯度弥散和梯度爆炸现象造成的。在较深层数的神经网络中，梯度信息由网络的末层逐层传向网络的首层时，传递的过程中会出现梯度接近于 0 或梯度值非常大的现象。网络层数越深，这种现象可能会越严重。

那么怎么解决深层神经网络的梯度弥散和梯度爆炸现象呢？一个很自然的想法是，既然浅层神经网络不容易出现这些梯度现象，那么可以尝试给深层神经网络添加一种回退到浅层神经网络的机制。当深层神经网络可以轻松地回退到浅层神经网络时，深层神经网络可以获得与浅层神经网络相当的模型性能，而不至于更糟糕。

通过在输入和输出之间添加一条直接连接的 Skip Connection可以让神经网络具有回退的能力。以 VGG13 深度神经网络为例，假设观察到 VGG13 模型出现梯度弥散现象，而10 层的网络模型并没有观测到梯度弥散现象，那么可以考虑在最后的两个卷积层添加 Skip Connection，如图 10.62 中所示。通过这种方式，网络模型可以自动选择是否经由这两个卷积层完成特征变换，还是直接跳过这两个卷积层而选择 Skip Connection，亦或结合两个卷积层和 Skip Connection 的输出。

2015 年，微软亚洲研究院何凯明等人发表了基于 Skip Connection 的深度残差网络(Residual Neural Network，简称 ResNet)算法，并提出了 18 层、34 层、50 层、101层、152 层的 ResNet-18、ResNet-34、ResNet-50、ResNet-101 和 ResNet-152 等模型，甚至成功训练出层数达到 1202 层的极深层神经网络。ResNet 在 ILSVRC 2015 挑战赛 ImageNet数据集上的分类、检测等任务上面均获得了最好性能，ResNet 论文至今已经获得超 25000的引用量，可见 ResNet 在人工智能行业的影响力。

10.12.1 ResNet 原理

ResNet 通过在卷积层的输入和输出之间添加 Skip Connection 实现层数回退机制，如下图 10.63 所示，输入通过两个卷积层，得到特征变换后的输出ℱ()，与输入进行对应元素的相加运算，得到最终输出ℋ()：
$$\mathcal{H}(x)=x+\mathcal{F}(x)$$
ℋ()叫作残差模块(Residual Block，简称 ResBlock)。由于被 Skip Connection 包围的卷积神经网络需要学习映射ℱ() = ℋ() − ，故称为残差网络。

为了能够满足输入与卷积层的输出ℱ()能够相加运算，需要输入的 shape 与ℱ()的shape 完全一致。当出现 shape 不一致时，一般通过在 Skip Connection 上添加额外的卷积运算环节将输入变换到与ℱ()相同的 shape，如图 10.63 中identity()函数所示，其中identity()以 1×1 的卷积运算居多，主要用于调整输入的通道数。

下图 10.64 对比了 34 层的深度残差网络、34 层的普通深度网络以及 19 层的 VGG 网络结构。可以看到，深度残差网络通过堆叠残差模块，达到了较深的网络层数，从而获得了训练稳定、性能优越的深层网络模型。

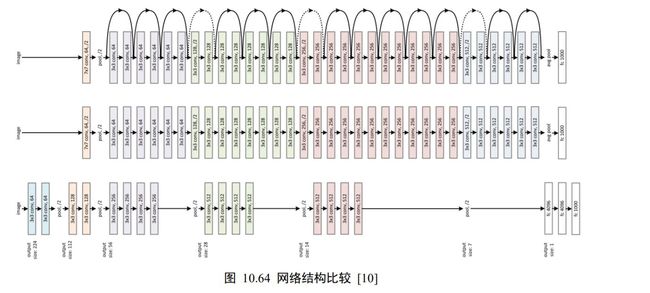
10.12.2 ResBlock 实现

深度残差网络并没有增加新的网络层类型，只是通过在输入和输出之间添加一条 Skip Connection，因此并没有针对 ResNet 的底层实现。在 TensorFlow 中通过调用普通卷积层即可实现残差模块。

首先创建一个新类，在初始化阶段创建残差块中需要的卷积层、激活函数层等，首先新建ℱ()卷积层，代码如下：

class BasicBlock(layers.Layer):
    # 残差模块类
    def __init__(self,filter_num,stride=1):
        super(BasicBlock,self).__init__()
        #f(x)包含了2个普通卷积层，创建卷积层1
        self.conv1=layers.Conv2D(filter_num,(3,3),strides=stride,padding='same')
        self.bn1=layers.BatchNormalzation()
        self.relu=layers.Activation('relu')
        # 创建卷积层2
        self.conv2=layers.Conv2D(filter_num,(3,3),strides=1,padding='same')
        self.bn2=layers.BatchNormalzation()

当ℱ()的形状与不同时，无法直接相加，我们需要新建identity()卷积层，来完成的形状转换。紧跟上面代码，实现如下：

        if stride!=1:#插入identify层
            self.downsample=Sequential()
            self.downsample.add(layers.Conv2D(filter_num,(1,1),strides=stride))
        else:# 否则，直接连接
            self.downsample=lambda x:x

在前向传播时，只需要将ℱ()与identity()相加，并添加 ReLU 激活函数即可。前向计算函数代码下：

    def call(self,inputs,training=None):
        out=self.conv1(inputs)
        out=self.bn1(out)
        out=self.relu(out)
        out=self.conv2(out)
        out=self.bn2(out)
        #输入通过identify()转换
        identify=self.downsample(inputs)
        # f(x)+x运算
        output=layers.add([out,identify])
        # 再通过激活函数并返回
        output=tf.nn.relu(output)
        return output

10.13 DenseNet

Skip Connection 的思想在 ResNet 上面获得了巨大的成功，研究人员开始尝试不同的Skip Connection 方案，其中比较流行的就是 DenseNet 。DenseNet 将前面所有层的特征图信息通过 Skip Connection 与当前层输出进行聚合，与 ResNet 的对应位置相加方式不同，DenseNet 采用在通道轴维度进行拼接操作，聚合特征信息。

如下图 10.65 所示，输入$X_0$ 通过$H_1$卷积层得到输出$X_1$，$X_1$与$X_0$ 在通道轴上进行拼接，得到聚合后的特征张量，送入$H_2$卷积层，得到输出$X_2$，同样的方法，2与前面所有层的特征信息$X_1$与$X_0$进行聚合，再送入下一层。如此循环，直至最后一层的输出$X_4$和前面所有层的特征信息：${\left\{{\mathbf{X}}_{\mathbf{i}}\right\}}_{i=0,1,2,3}$进行聚合得到模块的最终输出。这样一种基于 SkipConnection 稠密连接的模块叫做 Dense Block。

DenseNet 通过堆叠多个 Dense Block 构成复杂的深层神经网络，如图 10.66 所示。

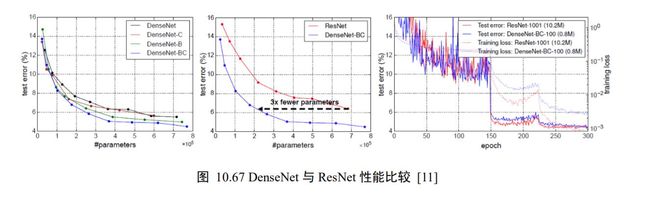
图 10.67 比较了不同版本的 DenseNet 的性能、DenseNet 与 ResNet 的性能比较，以及DenseNet 与 ResNet 训练曲线。

10.14 CIFAR10 与 ResNet18 实战

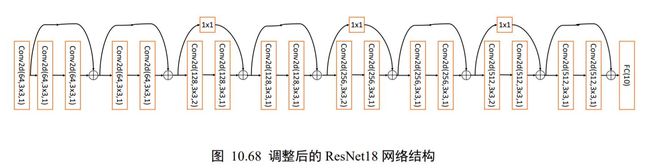
本节我们将实现 18 层的深度残差网络 ResNet18，并在 CIFAR10 图片数据集上训练与测试。并将与 13 层的普通神经网络 VGG13 进行简单的性能比较。

标准的 ResNet18 接受输入为224 × 224 大小的图片数据，我们将 ResNet18 进行适量调整，使得它输入大小为32 × 32，输出维度为 10。调整后的 ResNet18 网络结构如图 10.68所示。

首先实现中间两个卷积层，Skip Connection 1x1 卷积层的残差模块。代码如下：

class BasicBlock(layers.Layer):
    # 残差模块
    def __init__(self,filter_num,stride=1):
        super(BasicBlock,self).__init__()
        #第一个卷积单元
        self.conv1=layers.Conv2D(filter_num,(3,3),strides=stride,padding='same')
        self.bn1=layers.BatchNormalization()
        self.relu=layers.Activation('relu')
        #第二个卷积单元
        self.conv2=layers.Conv2D(filter_num,(3,3),strides=1,padding='same')
        self.bn2=layers.BatchNormalization()

        if stride!=1:#通过1*1卷积完成shape匹配
            self.downsample=Sequential()
            self.downsample.add(layers.Conv2D(filter_num,(1,1),strides=stride))
        else:# shape匹配，直接短接
            self.downsample=lambda x:x


    def call(self,inputs,training=None):
        #前向计算函数
        #[b,h,w,c],通过第一个卷积单元
        out=self.conv1(inputs)
        out=self.bn1(out)
        out=self.relu(out)
        #通过第二个卷积单元
        out=self.conv2(out)
        out=self.bn2(out)
        #通过identify模块
        identify=self.downsample(inputs)
        #2条路径输出直接相加
        output=layers.add([out,identify])
        output=tf.nn.relu(output)#激活函数
        
        return output

在设计深度卷积神经网络时，一般按照特征图高宽ℎ/逐渐减少，通道数逐渐增大的经验法则。可以通过堆叠通道数逐渐增大的 Res Block 来实现高层特征的提取，通过build_resblock 可以一次完成多个残差模块的新建。代码如下：

     def build_resblock(self,filter_num,blocks,stride=1):
        # 辅助函数，堆叠filter_num个BasicBlock
        res_blocks=Sequential()
        #只有第一个BasicBlock的步长可能不为1，实现下采样
        res_blocks.add(BasicBlock(filter_num,stride))
        
        for _ in range(1,blocks):#其他BasicBlock步长都为1
            res_blocks.add(BasicBlock(filter_num,stride=1))
            
        return res_blocks

下面我们来实现通用的 ResNet 网络模型。代码如下：

class ResNet(keras.Model):

    def build_resblock(self, filter_num, blocks, stride=1):
        # 辅助函数，堆叠filter_num个BasicBlock
        res_blocks = Sequential()
        # 只有第一个BasicBlock的步长可能不为1，实现下采样
        res_blocks.add(BasicBlock(filter_num, stride))

        for _ in range(1, blocks):  # 其他BasicBlock步长都为1
            res_blocks.add(BasicBlock(filter_num, stride=1))

        return res_blocks

    # 通用的ResNet实现类
    def __init__(self,layer_dims,num_classes=10):
        super(ResNet,self).__init__()
        #根网络，预处理
        self.stem=Sequential([
            layers.Conv2D(64,(3,3),strides=(1,1)),
            layers.BatchNormalization(),
            layers.Activation('relu'),
            layers.MaxPool2D(pool_size=(2,2),strides=(1,1),padding='same')
        ])
        #堆叠4个Block,每个Block包含了多个BasicBlock,设置步长不一样
        self.layer1=self.build_resblock(64,layer_dims[0])
        self.layer2=self.build_resblock(128,layer_dims[1],strifdes=2)
        self.layer3=self.build_resblock(256,layer_dims[2],strides=2)
        self.layer4=self.build_resblock(512,layer_dims[3],strides=2)

        #通过Pooling层将高宽降低为1*1
        self.avgpool=layers.GlobalAveragePooling2D()
        self.fc=layers.Dense(num_classes)

    def call(self,inputs,training=None):
        # 前向计算：通过根网络
        x=self.stem(inputs)
        # 一次通过4个模块
        x=self.layer1(x)
        x=self.layer2(x)
        x=self.layer3(x)
        x=self.layer4(x)

        #通过池化层
        x=self.avgpool(x)
        #通过全连接层
        x=self.fc(x)

通过调整每个 Res Block 的堆叠数量和通道数可以产生不同的 ResNet，如通过 64-64-128-128-256-256-512-512 通道数配置，共 8 个 Res Block，可得到 ResNet18 的网络模型。每个ResBlock 包含了 2 个主要的卷积层，因此卷积层数量是8 ∙ 2 =16，加上网络末尾的全连接层，共 18 层。创建 ResNet18 和 ResNet34 可以简单实现如下：

 def resnet18():
        #通过调整模块内部BasicBlock的数量和配置实现不同的ResNet
        return ResNet([2,2,2,2])

 def resnet34():
       #通过调整模块内部BasicBlock的数量和配置实现不同的ResNet
       return ResNet([3,4,6,3])

下面完成 CIFAR10 数据集的加载工作，代码如下：

(x,y), (x_test, y_test) = datasets.cifar10.load_data() # 加载数据集
y = tf.squeeze(y, axis=1) # 删除不必要的维度
y_test = tf.squeeze(y_test, axis=1) # 删除不必要的维度
print(x.shape, y.shape, x_test.shape, y_test.shape)
train_db = tf.data.Dataset.from_tensor_slices((x,y)) # 构建训练集
# 随机打散，预处理，批量化
train_db = train_db.shuffle(1000).map(preprocess).batch(512)
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test)) #构建测试集
# 随机打散，预处理，批量化
test_db = test_db.map(preprocess).batch(512)
第 10 章 卷积神经网络 58
# 采样一个样本
sample = next(iter(train_db))
print('sample:', sample[0].shape, sample[1].shape,
 tf.reduce_min(sample[0]), tf.reduce_max(sample[0]))

数据的预处理逻辑比较简单，直接将数据范围映射到 − 区间。这里也可以基于ImageNet 数据图片的均值和标准差做标准化处理。代码如下：

def preprocess(x, y):
 # 将数据映射到-1~1
 x = 2*tf.cast(x, dtype=tf.float32) / 255. - 1
 y = tf.cast(y, dtype=tf.int32) # 类型转换
 return x,y

网络训练逻辑和普通的分类网络训练部分一样，固定训练 50 个 Epoch。代码如下：

 for epoch in range(50): # 训练 epoch
 for step, (x,y) in enumerate(train_db):
 with tf.GradientTape() as tape:
 # [b, 32, 32, 3] => [b, 10],前向传播
 logits = model(x)
 # [b] => [b, 10],one-hot 编码
 y_onehot = tf.one_hot(y, depth=10)
 # 计算交叉熵
 loss = tf.losses.categorical_crossentropy(y_onehot, logits,
from_logits=True)
 loss = tf.reduce_mean(loss)
 # 计算梯度信息
 grads = tape.gradient(loss, model.trainable_variables)
 # 更新网络参数
 optimizer.apply_gradients(zip(grads, model.trainable_variables))

ResNet18 的网络参数量共 1100 万个，经过 50 个 Epoch 后，网络的准确率达到了79.3%。我们这里的实战代码比较精简，在精挑超参数、数据增强等手段加持下，准确率可以达到更高。