【NIOIP2016提高】天天爱跑步(LCA+树上差分)
近几年复赛最难的树上问题了。
几个月前做是参照题解的方法,用了可持久化线段树在树上无脑维护和统计。
当时的做法早已忘记,于是回过来自己做了做,其实远没有那么难做,只要发现一些奇妙的性质。
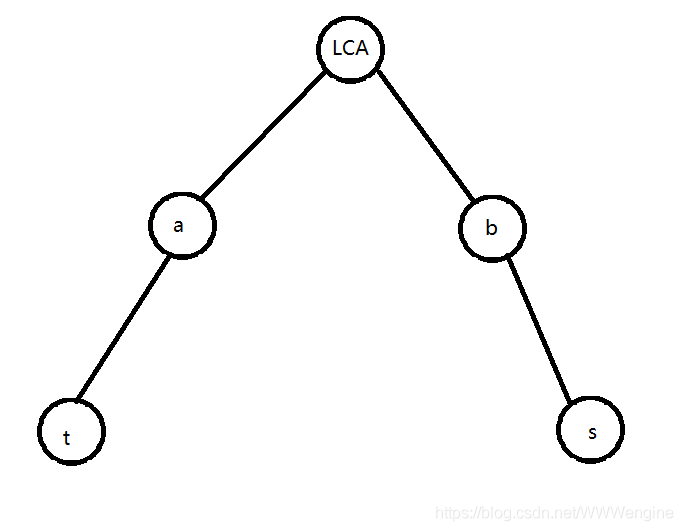
对于一个玩家s->t,如图。
对于图中a点的观察员存在这样一个式子:w(a)=dep(a)-dep(lca)+dep(s)-dep(lca)。
对于图中b点的观察员存在这样一个式子:w(b)=(dep(s)-dep(lca))-(dep(b)-dep(lca))。
转化一下,对于a,有:w(a)-dep(a)=dep(s)-2*dep(lca)。也就是对于lca往下走的路径上的点满足这个性质。
对于b,有:w(b)+dep(b)=dep(s)。也就是对于s往上走的路径上的点满足这个性质。
于是看似很麻烦的统计问题被化简了:等式左端只与点i本身有关,右端对于每个玩家是一个定值,“时间”的影响被去掉了。
于是统计的话,就是s->t这条路径上所有满足上式的a,b。
可以想见,统计答案就是走到一个点i,然后统计目前已有多少个“w(i)-dep(i)”,以及多少个“w(i)+dep(i)”。
利用差分的思想,对于从lca往下走的路径,在t处将“dep(s)-2*dep(lca)”的计数加一,在lca处将其计数减一,那么这一段路上遍
历到每个节点时,满足上述式子的加上对应的计数即可。
同理,对于从s往上走的路径,在s处将“dep(s)”的计数加一,在lca处将其计数减一。
开三个变长数组,一个名为work,用于存所有从v往lca走的“dep(s)-2*dep(lca)”以及lca,一个名为work2,用于存所有从s往上走
到lca的“dep(s)”以及lca。
最后一个名为del,用于存当前节点需要把哪一个值的计数减一。
以work2为例,我们后序遍历整棵树,假如现在遍历到了i,我们先遍历它的一个儿子j,然后当儿子j递归回来后,i的答案加
上“w(i)+dep(i)”和“w(i)-dep(i)”遍历j前后计数之差。
然后将i的所有del进行操作,并把i的del清空。接下来遍历下一个儿子。进行类似的操作。
当所有的儿子遍历完,再来对i的work2操作,每次依然是加上对应计数前后之差,并且每操作一个work2,就在对应的lca的del加
入本次操作的值,等回到lca时就执行del操作。
work与此完全一致,之所以要分开统计,是为了避免“w(i)-dep(i)”与“w(i)+dep(i)”相同的情况。
特殊情况:若lca满足”w(lca)+dep(lca)=dep(s)“和“w(lca)-dep(lca)=dep(s)-2*dep(lca)”中的一个,那么必然两个都满足,所以在加入
work和work2时要特判减一。
注:此代码用了树剖求LCA,理论上可以节约时间空间。
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=300005;
int N,M;
int np=0;
int w[MAXN];
int fa[MAXN];
int son[MAXN];
int top[MAXN];
int dep[MAXN];
int size[MAXN];
int last[MAXN];
int ans[MAXN];
int cnt[MAXN<<2];
struct edge{
int to,pre;
}E[MAXN<<1];
struct data{
int v,to;
};
vectorwork[MAXN];
vectorwork2[MAXN];
vectordel[MAXN];
char c,num[20];int ct;
void scan(int &x){
for(c=getchar();c<'0'||c>'9';c=getchar());
for(x=0;c>='0'&&c<='9';c=getchar())x=x*10+c-'0';
}
void print(int x){
ct=0;
if(!x)num[ct++]='0';
while(x){num[ct++]=x%10+'0',x/=10;}
while(ct--)putchar(num[ct]);
putchar(' ');
}
void add(int u,int v){
E[++np]=(edge){v,last[u]};
last[u]=np;
}
void dfs1(int x){
size[x]=1;
for(int p=last[x];p;p=E[p].pre){
int j=E[p].to;
if(j==fa[x])continue;
dep[j]=dep[x]+1; fa[j]=x;
dfs1(j); size[x]+=size[j];
if(size[j]>size[son[x]])son[x]=j;
}
}
void dfs2(int x,int tp){
top[x]=tp;
if(!son[x])return;
dfs2(son[x],tp);
for(int p=last[x];p;p=E[p].pre){
int j=E[p].to;
if(j==fa[x]||j==son[x])continue;
dfs2(j,j);
}
}
int LCA(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]dep[v])swap(u,v);
return u;
}
void calc(int x,int f){
int sz;
int ct1=cnt[w[x]-dep[x]+MAXN];//ct1是对应计数上一次的数量
for(int p=last[x];p;p=E[p].pre){
int j=E[p].to;
if(j==f)continue;
calc(j,x);//先遍历
ans[x]+=cnt[w[x]-dep[x]+MAXN]-ct1;//加上前后之差
sz=del[x].size();//执行del操作
for(int i=0;i