算法与数据结构-第二章:算法
1.什么是算法
算法是解决特定问题求解的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
1.1算法的特性
算法的五个基本特性 : 输入、输出 、 有穷性、确定性和可行性。
1.1.1 输入、输出
算法具有零个或多个输入,因为某些算法并不需要输入,比如hello World。
1.1.2 有穷性
有穷性:指算法在执行有限的步骤之后,自动结束而不会出现无限循环,并且每一个步骤在可接受的时间内完成。
1.1.3 确定性
确定性:算法的每一步骤都具有确定的含义 , 不会出现二义性 。
1.1.4 可行性
可行性:算法的每一步都必须是可行的 , 也就是说,每一步都能够通过执行有限
次数完成。
1.2.算法设计的要求
1.2.1正确性
正确性:算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。
正确性又分为4个层次:
1. 算法程序没有语法错误。
2. 算法程序对于合法的输入数据能够产生满足要求的输出结果。
3. 算法程序对于非法的输入数据能够得出满足规格说明的结果。
4 . 算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输 出结果。
对于这四层含义,层次 1 要求最低,但是仅仅没有语法错误实在谈环上是好算法 。 这就如同仅仅解决温饱, 不能算是生活幸福一样。 而层次 4 是最困难的,我们几乎不可能逐一验证所有的输入都得到正确的结果 。
因此算法的正确性在大部分情况下都不可能用程序来证明,而是用数学方法证明的。证明一个复杂算法在所4寄层次上都是正确的,代价非常昂贵。所以一般情况下,我们把层次 3 作为一个算法是否正确的标准。
1.2.2 可读性
可读性 : 算法设计的另一目的是为了便于阅读、 理解和交流。
1.2.3 健壮性
健壮性:当输入数据不合法时,算法也能做出相关处理, 而不是产生异常或莫名
其妙的结果。
1.2.4 时间效率高和存储量低
时间效率指的是算法的执行时间 , 对于同一个问题,如果有多个算法能够解决 ,执行时间短的算法效率高,执行时间长的效率低。 存储量需求指的是算法在执行过程中需要的最大存储空间, 主要指算法程序运行时所占用的内存或外部硬盘存储空间。
设计算法应该尽量满足时间效率高和存储量低的需求.
2. 算法效率的度量方法
2.1 事后统计法
该方法缺陷过多,不予采用。
2.2事前分析估算方法
事前分析估算方法:在计算机程序编制前,依据统计方法对算法进行估算。
一个用高级程序语言编写的程序在计算机上运行时所消耗
的时 间取决于下列因素:
1. 算法采用的策略、 方法。
2 . 编译产生的代码质量 。
3 . 问题的输入规模。
4. 机器执行指令的速度。
第 1 条当然是算法好坏的根本,第 2 条要 由软件来支持 , 第 4 条要看硬件性能。
也就是说 , 抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间,依赖于
算法的好坏和问题的输入规模。 所谓问题输入规模是指输入量的多少。
直接上代码,看例子:
package demo;
public class demo_suanfa {
public static void main(String[] args) {
int i,sum=0,n=100; //执行一次
for (i = 0; i <= n; i++) { //进入循环,执行了n+1次
sum=sum+i; //执行n次
}
System.out.println(sum); //执行一次
第二种算法:
int sum1=0,n1=100; //执行一次
sum1=(1+n)*n/2; //执行一次
System.out.println(sum1); //执行一次
}
}第一种算法,执行了 1+ ( n+1 ) +n+1 次 =2n+3 次 ; 而第二种算法,是
1+1+1=3 次。事实上两个算法的第一条和最后一条语句是一样的,所以我们关注的代码其实是中间的那部分,我们把循环看作一个整体 , 忽略头尾循环判断的开销, 那么这两个算法其实就是 n 次与 1 次的差距。算法好坏显而易见。
再用一个例子:
package demo;
public class demo_suanfa {
public static void main(String[] args) {
int i, j, x = 0, sum = 0, n = 100; // 一次
for (i = 0; i <= n; i++) { // 进入循环
for (j = 1; j <= n; j++) {
x++; //循环块,执行n*n次
sum = sum + x;
}
}
System.out.println(sum); //一次
}
}这个例子中, i 从 1 到 100 ,每次都要让 j 循环 100 次,而当中的 x++和 sum =
sum + x ; 其实就是 1+2+3+…+10000 ,也就是 100² 次,所以这个算法当中,循环部
分的代码整体需要执行 n² (忽略循环体头尾的开销)次。
显然这个算法的执行次数对于同样的输入规模 n = 100 , 要多于前面两种算法,这个算法的执行时间随着 n 的增加也将远远多于前面两个。
不用关心编写程序所用的程序设计语言是什么,也不关心这些程序将跑在什么样的计算机中,我们只关心它所实现的算法。这样,不计那些循环索引的递增和循环终止条件、 变量声明、打印结果等操作, 最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
2.3函数的渐进增长
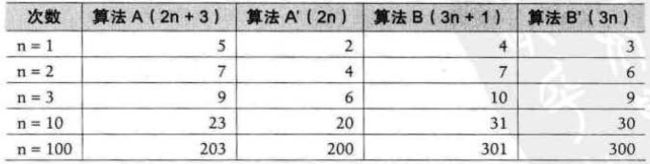
现在来判断一下,两个算法 A 和 B 哪个更好。 假设两个算法的输入规模都是n ,算法 A 要做 2 n + 3 次操作,可以理解为先有一个 n 次的循环 ,执行完成后,再有一于 n 次循环,最后有三次赋值或运算,共 2n + 3 次操作。 算法 B 要做 3n + 1 次操作。 你觉得它们谁更快呢?
准确说来,答案是不一定的(如下图所示)。
当 n = 1 时,算法 A 效率不如算法 B (次数比算法 B 要多一次)。 而当 n = 2 时,两者效率相同 i 当 n>2 时,算法 A 就开始优于算法 B 了,随着 n 的增加,算法 A 比算法 B 越来越好了: (执行的次数比 B 要少)。于是我们可以得出结论,算法 A 总体上要好过算法 B 。
得出这样的定义,输入规模 n 在没有限制的情况下,只要超过一个数值N ,这个函数就总是大于另一个函数,就称函数是渐近增长的。
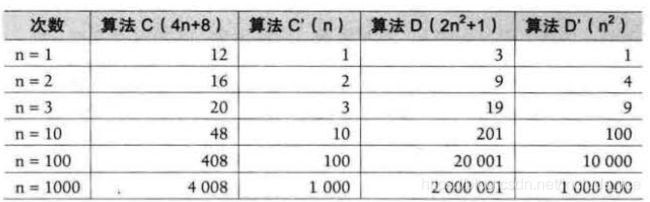
看第二个例子:
由表中数据得出,随着次数的增长,与最高次项相乘的常数并不重要,常数阶对结果影响就更小了。
判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项)的阶数。
基本就可以分析出:某个算法,随着 n 的增大,宫会越来越优于另一算法,或者越来越羞于另 一算法。这其实就是事前估算方法的理论依据 , 通过算法时间复杂度来估算算法时间效率。
3.时间复杂度
其实简单来说,就是执行完某个算法所使用的时间长短。
在进行算法分析时 , 语旬总的执行次撞 T ( n )是关子问题规模 n的函数,进而分析 T ( n )随 n 的变化情况并确定T(n)的数量级算法的时间复杂度.也就是算法的时闽量度,
记 作: T ( n )=O(f(n))。
用大写 O()来体现算法时间复杂度的记法,称之为大 0 记法。
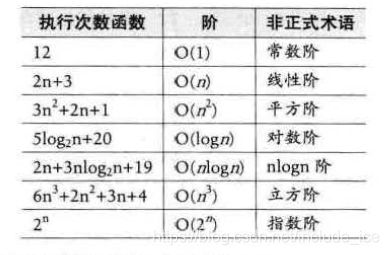
3.1 推导大O阶方法
推导大 O 阶 :
1.用常数 1 取代运行时间中的所有加法常数 。
2 .在修改后的运行次数函数中,只保留最高阶项 。
3.如果最高阶项存在且不是 1 ,则去除与这个项相乘的常敢 。
得到的结果就是大 O 阶。
3.1.1 常数阶
例子:
int sum=0,n=100; //1次
sum= (1+n)*n/2; //1次
System.out.println(sum); //1次这个算法的运行次数函数是f(n)=3,根据推导大O法,第一步就是将常数改为1,在它没有最高阶,或者最高阶就是常数,所以这个算法的时间复杂度为O(1)。
3.1.2 线性阶
线性阶的循环结构会复杂很多。要确定阶次,需要确定语句运行的次数,所以分析算法的复杂度,关键就是要分析循环结构的运行情况。
例子:
int i;
for (i=0;i上面例子时间复杂度为O(n)。
3.1.3 对数阶
例子:
int count = 1;
while (count < n) {
count = count * 2;
// 时间复杂皮为 O(1) 的程序步骤序列
}每次count*2 就会离n更近一分,也就是说 2X=n,得到x=log2n,所以时间复杂度为O(logn)。
3.1.4 平方阶
例子:
下面为一个嵌套循环,之前讲过的,也就是O(n)。
int i,j;
for ( i=0; i内部循环复杂度为O(n),外部循环复杂度也为O(n),所以整个算法复杂度为O(n²)。