算法导论 第十四章：区间树

区间树是一种对动态集合进行维护的红黑树，具体设计如下：

step1:基础数据结构

   我们选择的基础数据结构式红黑树，其中每个节点x包含一个区间域x.int,x的关键字为区间的低端点 x.int.low.

step2:附加信息

    每个节点x除了区间信息外，还包含一个值x.max，即以x为根的的子树中所有区间的断点的最大值

step3:对信息维护

   必须验证对含有n个节点的区间树的插入和删除都能在O(lgn)时间内完成，给定区间x.int 和 x.max 则有：x.max = max(x.int.high,x.left.max,x.right.max)

step4:设计新的操作

   我们唯一需要的新操作是INTERVAL-SEARCH(T，i),用以找出树T中覆盖区间i的那个节点。伪代码如下：

运行时间：O(lgn).

构建的区间树可以表示成如下：

完整代码如下：

#include
#include
using namespace std;
#define BLACK 0
#define RED 1

typedef struct interval{
	int low;
	int high;
	}interval;

typedef struct IntervalTNode{
	int key;
	bool color;
	IntervalTNode *parent;
	IntervalTNode *left;
	IntervalTNode *right;

	interval inte;  //additional information
	int max;        //additional information

	}IntervalTNode;

typedef struct IntervalTree{
	IntervalTNode *root;
	}IntervalTree;

//init sentine NIL
interval interval0={-1,-1};
IntervalTNode NILL={-1,BLACK,NULL,NULL,NULL,interval0,-1};
IntervalTNode *NIL=&NILL;          

/*-----------------------------------------------------------------------*/
int Max(int a,int b,int c)
{
	if(a>b)
		return a>c ? a:c;
	else
		return b>c ? b:c;
	}
bool Overlap(interval a,interval b)
{
	if(a.high < b.low || a.low > b.high)     // a & b do not overlap
		return 0;
	return 1;
	}
IntervalTNode *IntervalT_Search(IntervalTree *T,interval i)
{
	IntervalTNode *x=T->root;
	while(x!=NIL && !Overlap(i,x->inte))
	{ 
		if(x->left !=NIL && x->left->max>= i.low)
			x=x->left;
		else
			x=x->right;
		}
	return x;
}
/*-----------------------------------------------------------------------*/


void IntervalT_InorderWalk(IntervalTNode *x)
{
	if(x!=NIL)
 	 {  
		IntervalT_InorderWalk(x->left);
		cout<<"["<inte.low<inte.high<<"  ]";
		if(x->color==1)
			cout<<"     Red       "<max<max<right);
 		} 

	}

IntervalTNode *IntervalT_Minimum(IntervalTNode *x)
{
	while(x->left != NIL)
		x=x->left;
	return x;
	}

IntervalTNode *IntervalT_Successor(IntervalTNode *x)
{
     if(x->right != NIL)
         return IntervalT_Minimum(x->right);
     IntervalTNode *y = x->parent;
      while(y != NIL && x  == y->right){
         x = y;
         y = y->parent;
	    }
     return y;
	}

void Left_Rotate(IntervalTree *T,IntervalTNode *x)
{
	IntervalTNode *y=x->right;    //set y

	x->right=y->left;       //turn y's left subtree into x's right subtree
	if(y->left!=NIL)
		y->left->parent=x;

	y->parent=x->parent;     //link x's parent to y;
	if(x->parent == NIL)
		T->root=y;
	else if(x==x->parent->left)
		x->parent->left=y;
	else
		x->parent->right=y;

	y->left=x;               //put x on y's left
	x->parent=y;
	
	//maitaining additional information
	y->max=x->max;
	x->max=Max(x->inte.high,x->left->max,x->right->max);
	}

void Right_Rotate(IntervalTree *T,IntervalTNode *x)
{
	IntervalTNode *y=x->left;      //set y
	
	x->left=y->right;   //link x's left tree into y's right subtree;
	if(y->right !=NIL)
		y->right->parent=x;
	
	y->parent=x->parent;    //link x's parent to y
	if(x->parent == NIL)
		T->root=y;
	else if(x == x->parent->left)
		x->parent->left=y;
	else
		x->parent->right=y;
	
	y->right=x;         //put x on y's right
	x->parent=y;

	//Maintaining additional information
	y->max=x->max;
	x->max=Max(x->inte.high,x->left->max,x->right->max);

	}
void IntervalT_InsertFixup(IntervalTree *T,IntervalTNode *z)
{
	while(z->parent->color==RED)
	{
		if(z->parent == z->parent->parent->left)    
		{
			IntervalTNode *y=z->parent->parent->right;   
			if(y->color==RED)
			{  
				z->parent->color=BLACK;            //case 1
				y->color=BLACK;                    //case 1
				z->parent->parent->color=RED;      //case 1
				z=z->parent->parent;               //case 1
				}
			else
			{
			   	if(z==z->parent->right)
				{ 
					z=z->parent;                    //case 2
					Left_Rotate(T,z);               //case 2
				 	}
				z->parent->color=BLACK;             //case 3
				z->parent->parent->color=RED;       //case 3
				Right_Rotate(T,z->parent->parent);  //case 3
		 		} 
		 	}
		else
		{//a me as then clause with "right" and "left" exchanged  
			IntervalTNode *y=z->parent->parent->left;
			if(y->color==RED)
			{
				z->parent->color==BLACK;
				y->color=BLACK;
				z->parent->parent->color=RED;
				z=z->parent->parent;
		 	 	}
			else
			{
				if(z==z->parent->left)
				{
					z=z->parent;
					Right_Rotate(T,z);
			 	 	}
				z->parent->color=BLACK;
				z->parent->parent->color=RED;
				Left_Rotate(T,z->parent->parent);
			  	} 
			} 
		}   
	T->root->color=BLACK;      //turn the root to BLACK
	}
void IntervalT_Insert(IntervalTree *T,interval inte)
{
	IntervalTNode *z=new IntervalTNode();
	z->key=inte.low;
	z->max=inte.high;
	z->inte=inte;
	z->color =RED;   
	z->parent=NIL;
	z->left=NIL;
	z->right=NIL;

	IntervalTNode *y=NIL;        //y is the parent of x
	IntervalTNode *x=T->root;
	while(x != NIL)
	{ 
		x->max=max(x->max,z->max);     //Maintaining the max value of each node from z up to root
		y=x;
		if(z->key < x->key)
			x=x->left;
		else
			x=x->right;
		}   
	z->parent=y;   //link new node's parent node to y(y's child is NIL)
	if(y==NIL)
		T->root=z;
	else if(z->key < y->key)
		y->left=z;
	else
		y->right =z;
	IntervalT_InsertFixup(T,z);
	}

void IntervalT_DeleteFixup(IntervalTree *T,IntervalTNode *x)
{
	IntervalTNode *w;
	while(x!=T->root && x->color==BLACK)
	{
		if(x==x->parent->left)
	 	{
			w=x->parent->right;  //set w to x's sibling
			if(w->color==RED)      //case 1:x's sibling w is red
			{
				w->color=BLACK;
				x->parent->color=RED;
				Left_Rotate(T,x->parent);
				w=x->parent->right;
	 			}
			if(w->left->color==BLACK && w->right->color==BLACK)  
			{ //case 2:x's sibling w is black and both of w's children are black
				w->color=RED;
				x=x->parent;
				}
			else
			{ 
				if(w->right->color==BLACK)     
				{//case 3:x's sibling w is black,w's left child is red, and w's right child is black
					w->left->color=BLACK;
					w->color=RED;
					Right_Rotate(T,w);
					w=x->parent->right;
			 		}
				w->color=x->parent->color;      //case 4: x's sibling w is black,and w's right child is red
				x->parent->color=BLACK;         //.
				w->right->color=BLACK;         // .
				Left_Rotate(T,x->parent);      // .
				x=T->root;                     //case 4
				}
			}
		else
		{//Same as then clause with "right" and "left" exchanged
			w=x->parent->left;
			if(w->color==RED)
			{
				w->color=BLACK;
				x->parent->color=RED;
				Right_Rotate(T,x->parent);
				w=x->parent->left;
				} 
			if(w->left->color==BLACK && w->right->color==BLACK)
			{ 
				w->color=RED;
				x=x->parent;
				}
			else
			{
				if(w->left->color==BLACK)
				{
					w->right->color=BLACK;
					w->color=RED;
					Left_Rotate(T,w);
					w=x->parent->left;
			 	 	}
				w->color=x->parent->color;
				x->parent->color=BLACK;
				w->left->color=BLACK;
				Right_Rotate(T,x->parent);
				x=T->root;
	 			} 
	 		}
  		}
 	x->color=BLACK;
	}
void IntervalT_Delete(IntervalTree *T,IntervalTNode *z)
{
	IntervalTNode *x=NULL,*y=NULL,*g=NULL;
	
	if(z->left == NIL || z->right==NIL)
		y=z;
	else
		y=IntervalT_Successor(z);

	//maintaining additional information
	g=y->parent;
	g->max=g->inte.high;
	g=g->parent;
	while(g->max==y->max)
	{            
		g->max=Max(g->max,g->left->max,g->right->max);
		g=g->parent;
		}
	//delete y node
	if(y->left !=NIL)
		x=y->left;
	else
		x=y->right;
	x->parent=y->parent;

	if(y->parent==NIL)
		T->root=x;
	else if(y==y->parent->left)
		y->parent->left=x;
	else
		y->parent->right=x;

	if(y != z)
		z->key=y->key;

	if(y->color==BLACK)
		IntervalT_DeleteFixup(T,x);
	}


int main()
{
	interval A[]={{16,21},{8,9},{25,30},{5,8},{15,23},{17,19},{26,26},{0,3},{6,10},{19,20}};
	int n=sizeof(A)/sizeof(interval);
	
	cout<<"/*---------------------Create Interval Tree-------------------*/"<root=NIL;
	for(int i=0;iroot);
	cout<<"The root of the tree is:"<root->inte.low<<"   "<root->inte.high<>sInt.low>>sInt.high;
	IntervalTNode *sITNode=NIL;
	sITNode=IntervalT_Search(T,sInt);
	if(sITNode==NIL)
		cout<<"The searching interval doesn't exist in the tree."<inte.low<<"  "<inte.high<<"]";
		if(sITNode->color==0)
			cout<<"   color:RED     ";
		else
			cout<<"   color:BLACK   ";
		cout<<"Max:"<max<>dInt.low>>dInt.high;
	IntervalTNode  *dITNode=NIL;
	dITNode=IntervalT_Search(T,dInt);
	if(dITNode==NIL)
		cout<<"The deleting interval doesn't exist in the tree."<root);
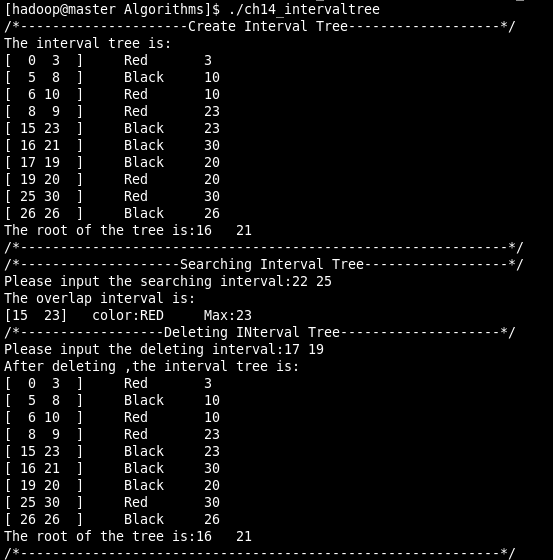
		cout<<"The root of the tree is:"<root->inte.low<<"   "<root->inte.high<

运行结果:

【注：若有错误，请指正~~~】