数据结构(Java实现)-详谈树与二叉树结构
1、树
1.1树的基本介绍
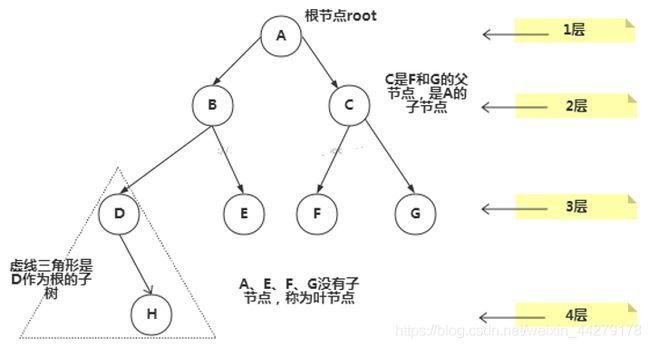
树(tree)是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
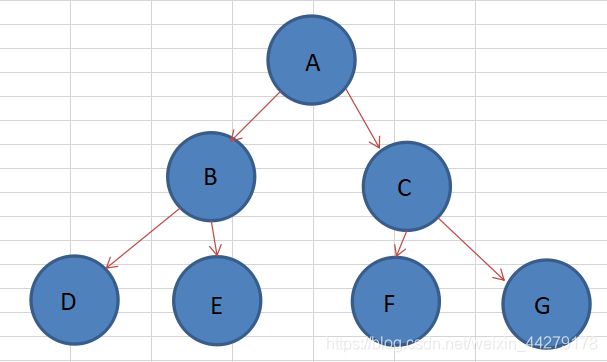
①、节点:上图的圆圈,比如A,B,C等都是表示节点。节点一般代表一些实体,在java面向对象编程中,节点一般代表对象。
②、边:连接节点的线称为边,边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在Java当中通常表示引用。
1.2树的常用术语
- 路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”。
- 根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
- 子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
- 叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的H、E、F、G都是叶子节点。
- 子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
- 节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
1.3为什么需要树这种结构
数组存储方式分析:
- 优点:通过下标可以直接访问元素,速度快。对于有序数组还可以使用二分查找提高检索速度。
- 缺点:如果要检索某个具体的值,或者插入值(按一定的顺序)会整体移动,效率较低(数组在创建的时候就已经确定了容量,如果超出了容量还要进行扩容操作)
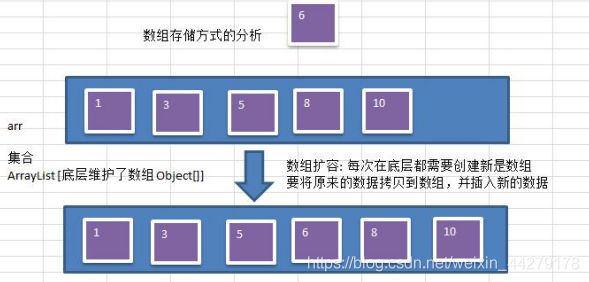
链式存储方式分析:
- 优点:在一定程度上对数组存储方式有了优化(比如:插入一个数值节点,只需要将待插入节点直接链接到链表中即可,删除效率也很高)
- 缺点:在进行检索时,效率仍然很低(比如检索某个特定的值,需要从头节点开始往后一个一个遍历)
树存储方式分析:
在数组和链式的存储方式上都有了一定的优化,能提高数据存储,读取的效率。(比如利用二叉排序树,既可以保证数据的检索速度,同时又保证了数据的插入、删除、修改的速度)
2、二叉树
2.1二叉树的基本介绍
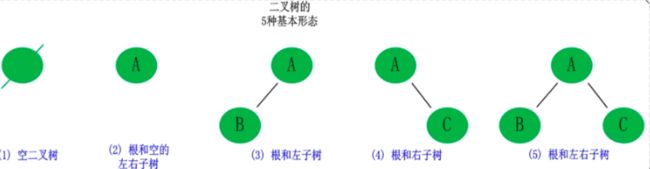
二叉树: 树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。二叉树的子节点分为左节点和右节点。
二叉树的五种基本形态:
二叉树的性质:
- 性质1:二叉树第i层上的结点数目最多为2^(i-1) (i>=1)
- 性质2:深度为k的二叉树至多有2^k-1个结点(k>=1)
- 性质3:包含n个结点的完全二叉树的深度至少为(log2^n)+1
- 性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
2.2满二叉树和完全二叉树
满二叉树:从形象上来说满二叉树是一个绝对的三角形,也就是说它的最后一层全部是叶子节点,其余各层全部是非叶子节点,如果用数学公式表示那么其节点数n=2^k-1其中k表示深度,也就是层数。也就是说满二叉树的节点数是一系列固定的数,比如说,1,3,7,15…如果节点数不是这个序列中的数,那么他肯定不是满二叉树,当然了,反之,是不成立的。
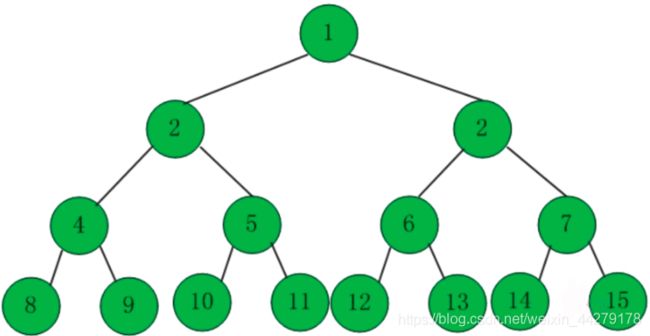
由于满二叉树的节点数必须是一个确定的数,而非任意数,他的使用受到了某些限制,为了打破另一个限制,我们定义一种特殊的满二叉树——完全二叉树。
完全二叉树:完全二叉树的节点个数是任意的,从形式上来说他是一个可能有缺失的三角形,但所缺部分肯定是右下角的某个连续部分。这样说不玩整,更准确来说,我们可以说他和满二叉树的区别是,他的最后一行可能不是完整的,但绝对是右方的连续部分缺失。可能听起来有点乱,用数学公式讲,对于K层的完全二叉树,其节点数的范围是2 ^ (k-1)-1
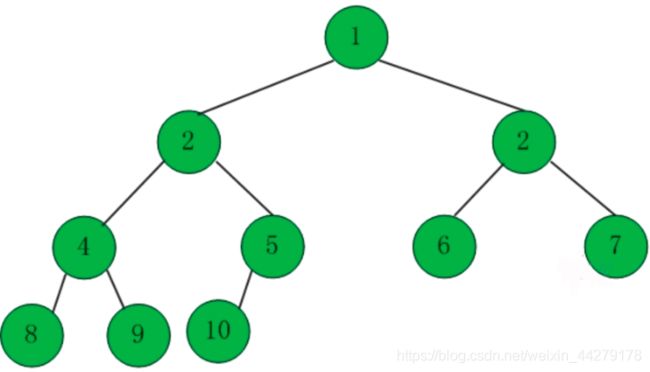
2.3二叉树的遍历
二叉树的遍历:
使用前序、中序和后序对二叉树进行遍历
- 前序遍历: 先输出父节点,再遍历左子树和右子树
- 中序遍历: 先遍历左子树,再输出父节点,再遍历右子树
- 后序遍历: 先遍历左子树,再遍历右子树,最后输出父节点
(看输出父节点的顺序,就确定是前序,中序还是后序)
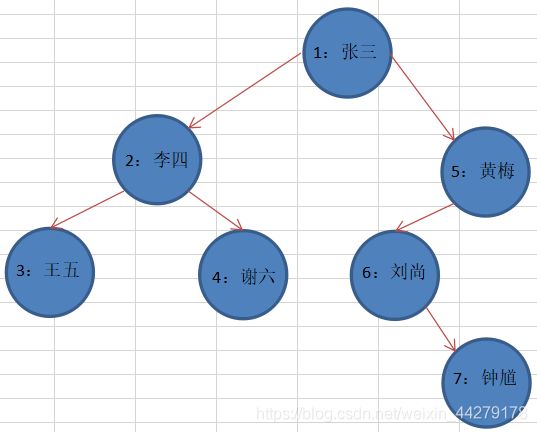
案例:创建学生节点(包含学生ID和姓名),将节点创建为以下二叉树并进行遍历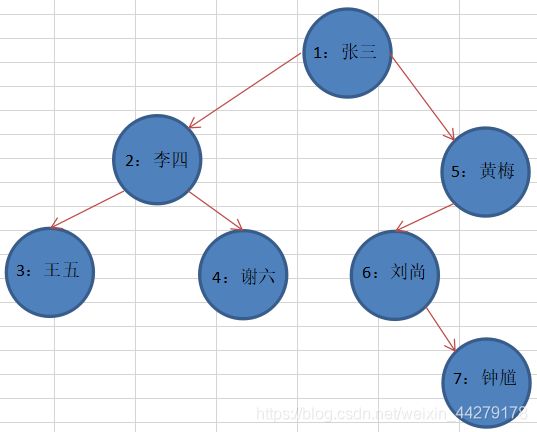
package com.zhukun;
//先创建StudentNode 结点类
class StudentNode {
private int no;//学生ID
private String name;//学生姓名
private StudentNode left; //默认null
private StudentNode right; //默认null
public StudentNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public StudentNode getLeft() {
return left;
}
public void setLeft(StudentNode left) {
this.left = left;
}
public StudentNode getRight() {
return right;
}
public void setRight(StudentNode right) {
this.right = right;
}
@Override
public String toString() {
return "StudentNode [no=" + no + ", name=" + name + "]";
}
//编写前序遍历的方法
public void preOrder() {
System.out.println(this); //先输出父结点
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//中序遍历方法
public void infixOrder() {
//递归向左子树中序遍历
if(this.left != null) {
this.left.infixOrder();
}
//输出父结点
System.out.println(this);
//递归向右子树中序遍历
if(this.right != null) {
this.right.infixOrder();
}
}
//后序遍历方法
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private StudentNode root;
public void setRoot(StudentNode root) {
this.root = root;
}
//前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
}
public class test{
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
StudentNode root = new StudentNode(1, "张三");
StudentNode node2 = new StudentNode(2, "李四");
StudentNode node3 = new StudentNode(3, "王五");
StudentNode node4 = new StudentNode(4, "谢六");
StudentNode node5 = new StudentNode(5, "黄梅");
StudentNode node6 = new StudentNode(6, "刘尚");
StudentNode node7 = new StudentNode(7, "钟馗");
//根据上面的二叉树图手动创建该二叉树
binaryTree.setRoot(root);
root.setLeft(node2);
root.setRight(node5);
node2.setLeft(node3);
node2.setRight(node4);
node5.setLeft(node6);
node6.setRight(node7);
//测试遍历
System.out.println("前序遍历"); // 1、2、3、4、5、6、7
binaryTree.preOrder();
System.out.println("中序遍历");//3、2、4、1、6、7、5
binaryTree.infixOrder();
System.out.println("后序遍历");//3、4、2、7、6、5、1
binaryTree.postOrder();
}
前序遍历
StudentNode [no=1, name=张三]
StudentNode [no=2, name=李四]
StudentNode [no=3, name=王五]
StudentNode [no=4, name=谢六]
StudentNode [no=5, name=黄梅]
StudentNode [no=6, name=刘尚]
StudentNode [no=7, name=钟馗]
中序遍历
StudentNode [no=3, name=王五]
StudentNode [no=2, name=李四]
StudentNode [no=4, name=谢六]
StudentNode [no=1, name=张三]
StudentNode [no=6, name=刘尚]
StudentNode [no=7, name=钟馗]
StudentNode [no=5, name=黄梅]
后序遍历
StudentNode [no=3, name=王五]
StudentNode [no=4, name=谢六]
StudentNode [no=2, name=李四]
StudentNode [no=7, name=钟馗]
StudentNode [no=6, name=刘尚]
StudentNode [no=5, name=黄梅]
StudentNode [no=1, name=张三]
2.3二叉树查找指定节点
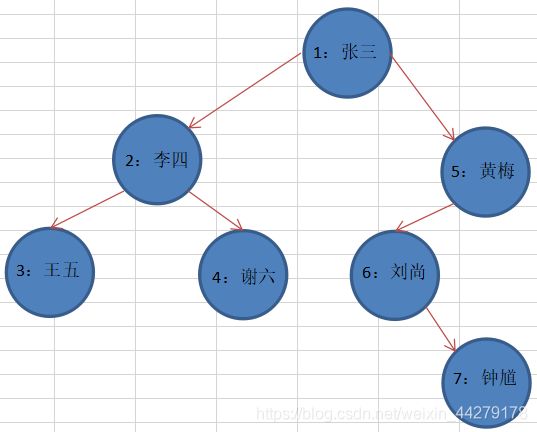
案例要求:
编写前序查找,中序查找和后序查找的方法。分别使用三种查找方法,查找no = 5的节点,并分析各种查找方式,分别比较了几次。
思路分析:
使用前序,中序,后序的方式来查询指定的结点
前序查找思路:
1.先判断当前结点的no是否等于要查找的
2.如果是相等,则返回当前结点
3.如果不等,则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
4.如果左递归前序查找,找到结点,则返回,否则继续判断当前结点的右子节点是否为空,如果不空,则继续向右递归前序查找.
中序查找思路:
1.判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
2.如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点,否则继续进行右子节点的递归中序查找
3.如果右子节点的递归中序查找找到,就直接返回,否则返回null
后序查找思路:
1.判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
2.如果找到,就返回,如果没有找到,就判断当前结点的右子节点是否为空,如果不为空,则右递归进行后序查找,如果找到,就返回
3.如果没找到,最后和当前结点进行,比如,如果是则返回,否则返回null
package com.zhukun;
//先创建StudentNode 结点
class StudentNode {
private int no;
private String name;
private StudentNode left; //默认null
private StudentNode right; //默认null
public StudentNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public StudentNode getLeft() {
return left;
}
public void setLeft(StudentNode left) {
this.left = left;
}
public StudentNode getRight() {
return right;
}
public void setRight(StudentNode right) {
this.right = right;
}
@Override
public String toString() {
return "StudentNode [no=" + no + ", name=" + name + "]";
}
//前序查找
/**
*
* @param no 查找no
* @return 如果找到就返回该Node ,如果没有找到返回 null
*/
public StudentNode preOrderSearch(int no) {
System.out.println("进入前序查找");
//比较当前结点是不是
if(this.no == no) {
return this;
}
//1.否则判断当前结点的左子节点是否为空,如果不为空,则递归前序查找
//2.如果左递归前序查找,找到结点,则返回
StudentNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {
//说明我们左子树找到
return resNode;
}
//1.左递归前序查找,找到结点,则返回,否继续判断,
//2.当前的结点的右子节点是否为空,如果不空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序遍历查找
public StudentNode infixOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归中序查找
StudentNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入中序查找");
//如果找到,则返回,如果没有找到,就和当前结点比较,如果是则返回当前结点
if(this.no == no) {
return this;
}
//否则继续进行右递归的中序查找
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//后序遍历查找
public StudentNode postOrderSearch(int no) {
//判断当前结点的左子节点是否为空,如果不为空,则递归后序查找
StudentNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {
//说明在左子树找到
return resNode;
}
//如果左子树没有找到,则向右子树递归进行后序遍历查找
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("进入后序查找");
//如果左右子树都没有找到,就比较当前结点是不是
if(this.no == no) {
return this;
}
return resNode;
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private StudentNode root;
public void setRoot(StudentNode root) {
this.root = root;
}
//前序查找
public StudentNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序查找
public StudentNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//后序查找
public StudentNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
}
public class test{
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
StudentNode root = new StudentNode(1, "张三");
StudentNode node2 = new StudentNode(2, "李四");
StudentNode node3 = new StudentNode(3, "王五");
StudentNode node4 = new StudentNode(4, "谢六");
StudentNode node5 = new StudentNode(5, "黄梅");
StudentNode node6 = new StudentNode(6, "刘尚");
StudentNode node7 = new StudentNode(7, "钟馗");
//先手动创建该二叉树,后面用递归的方式创建二叉树
binaryTree.setRoot(root);
root.setLeft(node2);
root.setRight(node5);
node2.setLeft(node3);
node2.setRight(node4);
node5.setLeft(node6);
node6.setRight(node7);
//测试查找
//前序查找
//前序查找比较的次数 :5
System.out.println("前序查找~~~");
StudentNode resNode1 = binaryTree.preOrderSearch(5);
if (resNode1 != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode1.getNo(), resNode1.getName());
} else {
System.out.printf("没有找到 no = %d 的学生", 5);
}
//中序遍历查找
//中序遍历7次
System.out.println("中序遍历方式~~~");
StudentNode resNode2 = binaryTree.infixOrderSearch(5);
if (resNode2 != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode2.getNo(), resNode2.getName());
} else {
System.out.printf("没有找到 no = %d 的学生", 5);
}
//后序遍历查找
//后序遍历查找的次数 6次
System.out.println("后序遍历方式~~~");
StudentNode resNode3 = binaryTree.postOrderSearch(5);
if (resNode3 != null) {
System.out.printf("找到了,信息为 no=%d name=%s\n", resNode3.getNo(), resNode3.getName());
} else {
System.out.printf("没有找到 no = %d 的学生", 5);
}
}
}
前序查找~~~
进入前序查找
进入前序查找
进入前序查找
进入前序查找
进入前序查找
找到了,信息为 no=5 name=黄梅
中序遍历方式~~~
进入中序查找
进入中序查找
进入中序查找
进入中序查找
进入中序查找
进入中序查找
进入中序查找
找到了,信息为 no=5 name=黄梅
后序遍历方式~~~
进入后序查找
进入后序查找
进入后序查找
进入后序查找
进入后序查找
进入后序查找
找到了,信息为 no=5 name=黄梅
2.3二叉树删除指定节点
要求:
- 如果删除的节点是叶子节点,则删除该节点
- 如果删除的节点是非叶子节点,则删除该子树.
思路分析:
首先先处理:
考虑如果树是空树root,如果只有一个root结点,则等价将二叉树置空
//然后进行下面步骤
1.因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否是需要删除节点,而不能去判断当前这个结点是不是需要删除的节点.
2.如果当前节点的左子节点不为空,并且左子结点就是要删除结点,就将his.left=null; 并且返回(结束递归删除)
3.如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this.right=null;并且返回(结束递归删除)
4.如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
5.如果第4步也没有删除结点,则应当向右子树进行递归删除.
//先创建StudentNode 结点
class StudentNode {
private int no;
private String name;
private StudentNode left; //默认null
private StudentNode right; //默认null
public StudentNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public StudentNode getLeft() {
return left;
}
public void setLeft(StudentNode left) {
this.left = left;
}
public StudentNode getRight() {
return right;
}
public void setRight(StudentNode right) {
this.right = right;
}
@Override
public String toString() {
return "StudentNode [no=" + no + ", name=" + name + "]";
}
public void preOrder() {
System.out.println(this); //先输出父结点
//递归向左子树前序遍历
if(this.left != null) {
this.left.preOrder();
}
//递归向右子树前序遍历
if(this.right != null) {
this.right.preOrder();
}
}
//递归删除结点
//1.如果删除的节点是叶子节点,则删除该节点
//2.如果删除的节点是非叶子节点,则删除该子树
public void delNode(int no) {
//思路
/*
* 1. 因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除结点,而不能去判断当前这个结点是不是需要删除结点.
2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
3. 如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
4. 如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
5. 如果第4步也没有删除结点,则应当向右子树进行递归删除.
*/
//2. 如果当前结点的左子结点不为空,并且左子结点 就是要删除结点,就将this.left = null; 并且就返回(结束递归删除)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3.如果当前结点的右子结点不为空,并且右子结点 就是要删除结点,就将this.right= null ;并且就返回(结束递归删除)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4.我们就需要向左子树进行递归删除
if(this.left != null) {
this.left.delNode(no);
}
//5.则应当向右子树进行递归删除
if(this.right != null) {
this.right.delNode(no);
}
}
}
//定义BinaryTree 二叉树
class BinaryTree {
private StudentNode root;
public void setRoot(StudentNode root) {
this.root = root;
}
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉树为空,无法遍历");
}
}
//删除结点
public void delNode(int no) {
if(root != null) {
//如果只有一个root结点, 这里立即判断root是不是就是要删除结点
if(root.getNo() == no) {
root = null;
} else {
//递归删除
root.delNode(no);
}
}else{
System.out.println("空树,不能删除~");
}
}
}
public class test{
public static void main(String[] args) {
//先需要创建一颗二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的结点
StudentNode root = new StudentNode(1, "张三");
StudentNode node2 = new StudentNode(2, "李四");
StudentNode node3 = new StudentNode(3, "王五");
StudentNode node4 = new StudentNode(4, "谢六");
StudentNode node5 = new StudentNode(5, "黄梅");
StudentNode node6 = new StudentNode(6, "刘尚");
StudentNode node7 = new StudentNode(7, "钟馗");
//先手动创建该二叉树,后面用递归的方式创建二叉树
binaryTree.setRoot(root);
root.setLeft(node2);
root.setRight(node5);
node2.setLeft(node3);
node2.setRight(node4);
node5.setLeft(node6);
node6.setRight(node7);
//删除前
System.out.println("删除前,前序遍历");
binaryTree.preOrder();
//删除
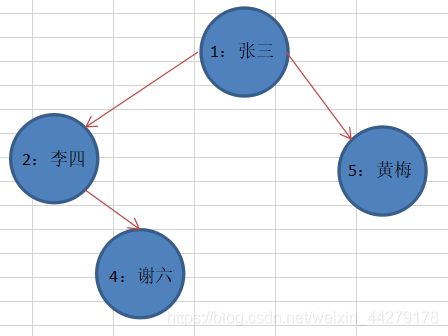
System.out.println("删除no=3的节点和no=6子树");
binaryTree.delNode(3);
binaryTree.delNode(6);
//删除后
System.out.println("删除后,前序遍历");
binaryTree.preOrder();
}
}
删除前,前序遍历
StudentNode [no=1, name=张三]
StudentNode [no=2, name=李四]
StudentNode [no=3, name=王五]
StudentNode [no=4, name=谢六]
StudentNode [no=5, name=黄梅]
StudentNode [no=6, name=刘尚]
StudentNode [no=7, name=钟馗]
删除no=3的节点和no=6子树
删除后,前序遍历
StudentNode [no=1, name=张三]
StudentNode [no=2, name=李四]
StudentNode [no=4, name=谢六]
StudentNode [no=5, name=黄梅]
欢迎持续关注!
个人博客站:jQueryZK Blog