数据结构笔记（六）——散列（Hash Table）之开放定址法（3）

前一篇讲了分离链接法，它的实现简单易懂，但是分离链接法需要指针，需要实现链表，给新单元分配地址也需要时间，因此速度有所下降。这一节的开放定址法不用链表来解决冲突，而是当遇到冲突时，尝试选择其他位置，直到找到一个空位置。，且F(0)=0.函数F为冲突解决方法。可以看到，数据将会被全部放入表中（不会有一个额外的链表用来存储数据），装填因子λ应该低一点（<0.5），这样出现冲突的可能会稍低一点。

对于F（i）的选择有很多种，比如就是线性探测法，就是平方探测法。

线性探测法就是冲突函数为线性的探测方法。通过计算公式可以看出，我们从hash函数计算的位置处开始逐个遍历查看是否有空位置，只要还有空位置，我们就可以找到放置X的地方，但当表差不多满了的时候，找空位置的代价就是N了。甚至当表相对比较空的时候，占据的单元也会形成一个区块（称为一次聚集），我们想要找到下一个空位置就先要跳过（查找过）这些聚集的地方。可以证明，不成功的查找和成功的查找需要的探测次数分别为1/2(1+1/(1-λ)^2)和1/2(1+1/(1-λ）)，分析表明，如果表有多于一半被填满的话，探测的次数就太多了。λ=0.5时，插入的平均探测次数为2.5，成功的插入需要1.5次，λ=0.75时平均就需要8.5次，所以在用线性探测法时，应使λ<0.5.

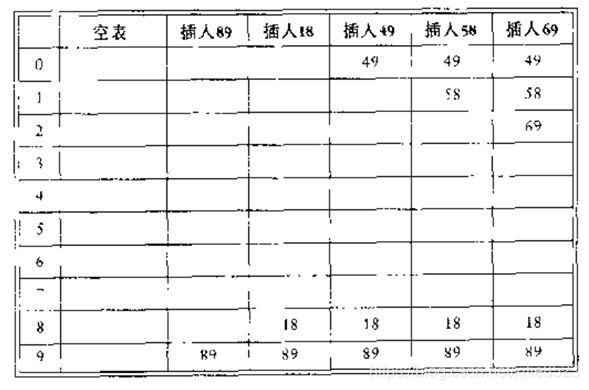
                    线性探测法，hash（x）=X mod 10，F(i)=i，依次插入89,18,49,58,69

平方探测法是冲突函数为二次函数的探测方法。同样，当表中被填充的位置超过一半时，其性能也会迅速下降，由于平方探测是以1,4,9,16为间隔探测空位置的，有时即使表中有空位，我们却无法找到也无法插入某个新元素。但是当表中至少一半为空，且表的大小为素数时，我们可以保证总能插入一个新元素。哪怕比表的一半多一个的位置被填满，我们就无法保证可以成功插入了。

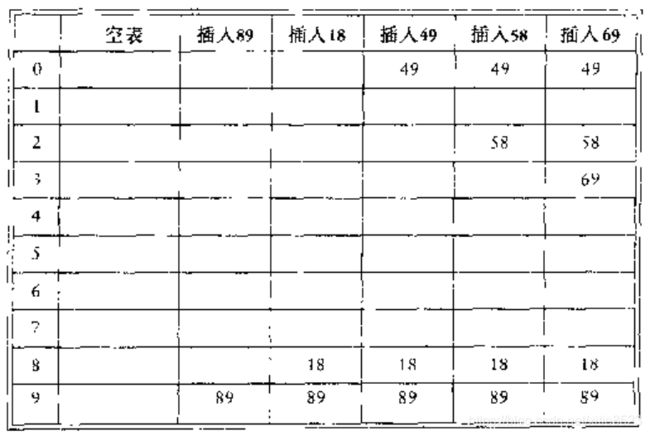
                 平方探测法，hash（x）=X mod 10，F(i)=i*i，依次插入89,18,49,58,69

另外，我们想删除某个元素也不是很容易了，如果我们删除89，那么当我们查找49的时候，第一个探测的位置是9，这个位置为空，程序将会返回未查找到这个结果，所以我们需要懒惰删除，额外添加一个标记，标记89为删除了的而不删掉它，这样可以使各个程序正常运行。

代码：

HashAdr.h

#pragma once
#include
#define MINSIZE 5
using namespace std;
typedef int ElementType;
typedef unsigned int Index;
typedef Index Position;
struct HashAdr;
typedef HashAdr *HashTb;
HashTb initialize(int size);
void insert(HashTb ht, ElementType e);
Position find(HashTb ht, ElementType e);
void deleteX(HashTb ht, ElementType e);
void destory(HashTb ht);

enum kind{Legitimate,Empty,Deleted};
struct Cell 
{
	ElementType element;
	enum kind info;
};
struct HashAdr 
{
	Cell* table;
	int table_size;
};
int nextPrime(int x);
int hashFunc(int x, int table_size);

HashAdr.cpp

#include "stdafx.h"
#include "HashAdr.h"
HashTb initialize(int size)
{
	if (sizetable_size = nextPrime(size);
	ht->table = (Cell*)malloc(sizeof(Cell)*ht->table_size);
	if (ht->table==nullptr)
	{
		free(ht);
		cerr << "out of space";
		return nullptr;
	}
	for (int i=0;itable_size;++i)
	{
		ht->table[i].info = Empty;
	}
	return ht;
}
void insert(HashTb ht, ElementType e)
{
	Position pos = find(ht, e);
	if (ht->table[pos].info!=Legitimate)
	{
		ht->table[pos].element = e;
		ht->table[pos].info = Legitimate;
	}
}
Position find(HashTb ht, ElementType e)
{
	Position pos = hashFunc(e,ht->table_size);
	int i = 0;
	while (ht->table[pos].info != Empty&&ht->table[pos].element!=e)//判断为空在前
	{
		pos += (2 * ++i - 1);//f(i)-f(i-1)=2i-1
		if (pos>=ht->table_size)
		{
			pos -= ht->table_size;
		}
	}
	return pos;
}
void deleteX(HashTb ht, ElementType e)
{
	Position pos = find(ht, e);
	if (ht->table[pos].info==Legitimate)
	{
		ht->table[pos].info = Deleted;
	}
}
void destory(HashTb ht)
{
	if (ht!=nullptr)
	{
		if (ht->table != nullptr)
		{
			free(ht->table);
		}
		free(ht);
	}
	

}
int nextPrime(int x)
{
	if (x % 2 == 0)
	{
		x++;//变成奇数
	}
	for (;; x += 2)//偶数不是素数
	{
		bool flag = true;
		for (int i = 3; i*i <= x; i += 2)
		{
			if (x%i == 0)
			{
				flag = false;
				break;
			}
		}
		if (flag)
		{
			return x;
		}
	}
	return 0;
}
int hashFunc(int x, int table_size)
{
	return x%table_size;
}

test.cpp

// HashTable.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "HashAdr.h"
#include
int main()
{
	HashTb ht = initialize(26);
	int input;
	cout << "input: " << endl;
	cin >> input;
	while (input!=-1)
	{
		insert(ht, input);
		cin >> input;
	}
	cout << "table size:" << ht->table_size << endl;
	if (find(ht,33))
	{
		cout << "yes" << endl;
		deleteX(ht, 33);
	}
	else
	{
		cout << "no" << endl;
	}
	destory(ht);
    return 0;
}

结果：