机器学习2 分类与逻辑回归

​ 分类问题和线性回归问题很像，只是在分类问题中我们预测的 y y 值包含在一个小的离散数据集里。首先，认识一下二元分类(binary classification)，在二元分类中， y y 的取值只能是 0 和 1。例如，我们要做一个垃圾邮件分类器，则 x(i) x ( i ) 为邮件的特征，而对于 y y ，当它为1，则为垃圾邮件，为0 则表示邮件为正常邮件。所以 0 称之为负类（negative class），1为正类（positive class） 。

逻辑回归

​ 我们知道线性回归问题只能预测连续的值，而分类问题，往往是分成几个类，或者是某一类（ y=1 y = 1 ），不是某一类（ y=0 y = 0 ）。对于后者，若已知 y∈{0,1} y ∈ { 0 , 1 } ，则 hθ(x) h θ ( x ) 大于1，或者小于0都是没有意义的。To fix this，我们选择：

hθ(x)=g(θTx)=11+eθTx h θ ( x ) = g ( θ T x ) = 1 1 + e θ T x

g(z)=11+ez g ( z ) = 1 1 + e z

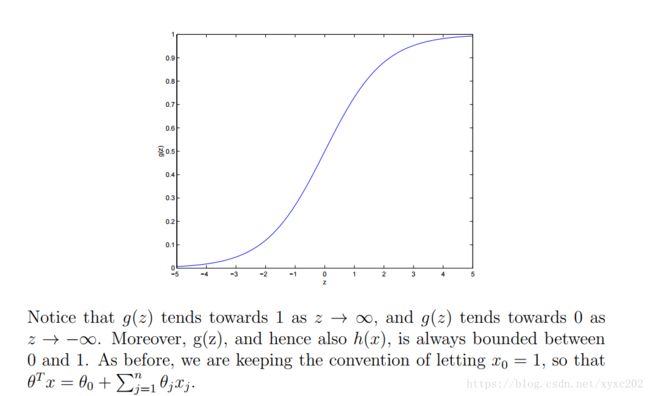
g(z) g ( z ) 是逻辑函数，或者叫==sigmoid函数== ，如下图所示。

​ 虽然其他平滑函数，只要能使 hθ(x) h θ ( x ) 的值限制到 [0,1] 也是可以的，其实选择sigmoid函数是很自然的，具体将在 讲GLM 算法的时候讲。

​ g(z) g ( z ) 的导数有个很重要的属性：

g(z)′====ddz11+eze−z(1+e−z)211+e−z−1(1+e−z)2g(z)[1−g(z)](119)(120)(121)(122) (119) g ( z ) ′ = d d z 1 1 + e z (120) = e − z ( 1 + e − z ) 2 (121) = 1 1 + e − z − 1 ( 1 + e − z ) 2 (122) = g ( z ) [ 1 − g ( z ) ]

​ 那么，给定逻辑回归模型，我们如何拟合出合适的 θ θ ? 根据由最大似然估计得到 LSR，我们赋予分类模型一组概率假设，然后通过最大似然函数得到合适的参数。

p(y=1|x;θ)p(y=0|x;θ)==hθ(x)1−hθ(x)(123)(124) (123) p ( y = 1 | x ; θ ) = h θ ( x ) (124) p ( y = 0 | x ; θ ) = 1 − h θ ( x )

​ 合并起来可以写成下面的形式：

p(y|x;θ)=(hθ(x))y(1−hθ(x))1−y p ( y | x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y

​ 假设 m m 个训练样本是独立的，则参数的似然函数如下：

L(θ)===p(y⃗ |X;θ)∏i=1mp(y(i)|x(i);θ)∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)(125)(126)(127) (125) L ( θ ) = p ( y → | X ; θ ) (126) = ∏ i = 1 m p ( y ( i ) | x ( i ) ; θ ) (127) = ∏ i = 1 m ( h θ ( x ( i ) ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i )

ℓ(θ)==lnL(θ)∑i=1m[y(i)lnhθ(x(i))+(1−y(i))ln(1−hθ(x(i)))](31)(32) (31) ℓ ( θ ) = l n L ( θ ) (32) = ∑ i = 1 m [ y ( i ) l n h θ ( x ( i ) ) + ( 1 − y ( i ) ) l n ( 1 − h θ ( x ( i ) ) ) ]

​ 最大化似然函数的方法有两种。一种和线性回的推导相似，梯度上升的方法；另一种是牛顿法。

（1）梯度上升法

​ 用向量来表示的话 ，我们可以用下式来更新参数：

θ:=θ+α∇θℓ(θ) θ := θ + α ∇ θ ℓ ( θ )

​ 需要注意的是，这里是 + 不是 - ，因为是最大化似然函数。下面先假设只有一个训练样本 (x,y) ( x , y ) ，使用随机梯度上升规则。

∂ℓ(θ)∂θj=====∂∂θj[ylnhθ(x)+(1−y)ln(1−hθ(x))][y1hθ(x)−(1−y)11−hθ(x)]∂hθ(x)∂θj[y1g(θTx)−(1−y)11−g(θTx)]g(θTx)(1−g(θTx))∂θTx∂θj(y(1−g(θTx))−(1−y)g(θTx))xj(y−hθ(x))xj(33)(34)(35)(36)(37) (33) ∂ ℓ ( θ ) ∂ θ j = ∂ ∂ θ j [ y l n h θ ( x ) + ( 1 − y ) l n ( 1 − h θ ( x ) ) ] (34) = [ y 1 h θ ( x ) − ( 1 − y ) 1 1 − h θ ( x ) ] ∂ h θ ( x ) ∂ θ j (35) = [ y 1 g ( θ T x ) − ( 1 − y ) 1 1 − g ( θ T x ) ] g ( θ T x ) ( 1 − g ( θ T x ) ) ∂ θ T x ∂ θ j (36) = ( y ( 1 − g ( θ T x ) ) − ( 1 − y ) g ( θ T x ) ) x j (37) = ( y − h θ ( x ) ) x j

⇒θ:=θ+α(y−hθ(x))xj ⇒ θ := θ + α ( y − h θ ( x ) ) x j

​ 如果我们将其与LMS更新规则进行比较，我们会发现它看起来差不多; 但这不是相同的算法，因为 hθ(x(i)) h θ ( x ( i ) ) 现在被定义为 θTx(i) θ T x ( i ) 的非线性函数。 尽管如此，我们最终得到了相同的更新规则以获得相当不同的算法和学习问题。这是巧合吗，具体原因请移步GLM Model。

（1 12 1 2 ）插叙：感知学习算法

​ 我们现在离题谈论一个具有一定历史意义的算法， 考虑修改逻辑回归的方法以“强制”它输出0或1或精确值。 要做到这一点，将 g g 的定义更改为阈值函数似乎很自然：

g(z)={10(ifz≥0)(ifz<0) g ( z ) = { 1 ( i f z ≥ 0 ) 0 ( i f z < 0 )

​ 同样，令 hθ(x)=g(θTx) h θ ( x ) = g ( θ T x ) ， g g 的定义如上式（22），同样用更新规则：

θ:=θ+α(y−hθ(x))xj θ := θ + α ( y − h θ ( x ) ) x j ，这样便得到了==感知学习算法== （perceptron learning algorithm）

​ 在20世纪60年代，这种“感知机”被认为是解释大脑中各个神经元如何工作的粗略模型。尽管感知器可能在美学上与我们所讨论的其他算法相似，但它实际上是一种非常不同类型的算法，而不是逻辑回归和LSR。

（2）牛顿法

​ 回到逻辑回归，另一种最大化似然函数的方法是==牛顿法== (Newton’s method)。

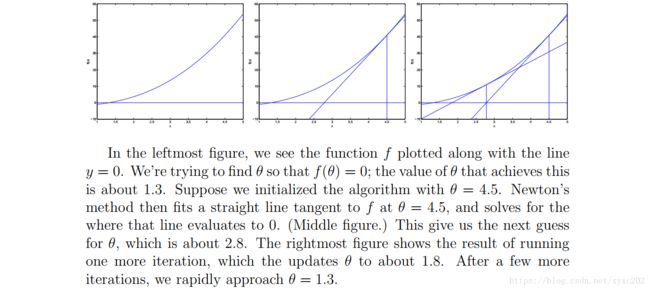
​ 牛顿法的核心思想是找 0。假设有函数 f:R↦R f : R ↦ R . 我们要找到一个 θ θ 使得 f(θ)=0 f ( θ ) = 0 成立， θ∈R θ ∈ R ，是一个实数。此时牛顿法的更新规则如下：

θ:=θ−f(θ)f′(θ) θ := θ − f ( θ ) f ′ ( θ )

​ 这种方法有一个自然的解释，我们可以把它看作是通过线性函数逼近函数 f f ，线性函数在当前猜测 θ θ 处与 f f 相切，求解线性函数等于零的位置，并让 θ θ 的下一个猜测 θ θ 成为线性函数为零的地方。下面是牛顿法的图解：

​ 牛顿方法给出了一种获得 f(θ)=0 f ( θ ) = 0 的方法。如果我们想用它来最大化函数 ℓ ℓ 该怎么办呢？函数 ℓ ℓ 的最大值对应其一阶导数 ℓ′ ℓ ′ 为零的点。 因此，可以令

f(θ)=ℓ′(θ) f ( θ ) = ℓ ′ ( θ ) 。我们同样用更新规则的方式最大化 ℓ ℓ ：

θ:=θ−ℓ′(θ)ℓ′′(θ) θ := θ − ℓ ′ ( θ ) ℓ ″ ( θ )

​ 最后，在我们的逻辑回归数据中， θ θ 是向量，因此我们需要将牛顿方法推广到这些数据上。 牛顿法对这种多维数据的推广（称为==Newton-Raphson法==）由下式给出：

θ:=θ−H−1∇θℓ(θ) θ := θ − H − 1 ∇ θ ℓ ( θ )

​ H H 是 n×n n × n 的矩阵（实际上，如果加上截距项，则大小为 (n+1)×(n+1) ( n + 1 ) × ( n + 1 ) ）。 H H called ==Hessian== , 它的项的形式如下：

Hij=∂2ℓ(θ)∂θi∂θj H i j = ∂ 2 ℓ ( θ ) ∂ θ i ∂ θ j

​ 牛顿法通常比 (batch) gradient descent更快收敛，并且需要更少的迭代次数就能达到非常接近最小值。 然而，牛顿法的一次迭代可能比一次梯度下降迭代代价更昂贵，因为它需要找到一个 n×n n × n 的Hessian矩阵，并求逆。但只要 n n 不是太大，整体通常要快得多。牛顿方法用于最大化逻辑回归对数似然函数 ℓ(θ) ℓ ( θ ) 时，称为Fisher scoring 。

分类和逻辑回归(Classification and logistic regression)
斯坦福机器学习课程Lecture 1（cs229-notes1）