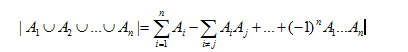Leetcode-1201丑数III
请你帮忙设计一个程序,用来找出第 n 个丑数。
丑数是可以被 a 或 b 或 c 整除的 正整数。
示例 1:
输入:n = 3, a = 2, b = 3, c = 5
输出:4
解释:丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。
示例 2:
输入:n = 4, a = 2, b = 3, c = 4
输出:6
解释:丑数序列为 2, 3, 4, 6, 8, 9, 12... 其中第 4 个是 6。
示例 3:
输入:n = 5, a = 2, b = 11, c = 13
输出:10
解释:丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。
示例 4:
输入:n = 1000000000, a = 2, b = 217983653, c = 336916467
输出:1999999984
提示:
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/ugly-number-iii
解题思路:
在[0, k]内,能被数a整除的数的个数是k/a. 那么同时能被a、b整除的个数呢?答案是 k/a + k/b - k/(ab最小公倍数). 那么能被a||b||c整除的呢?答案是 k/a + k/b + k/c - k/(ab最小公倍数) - k/(ac最小公倍数) - k/(bc最小公倍数) + k/(abc最小公倍数).
既然能求出能被a、b、c整除的个数,那么我们就可以使用二分进行求解,二分的目标就是所求答案,true条件为能被a、b、c整除的个数达到n个。
那么求a、b的最小公倍数怎么做?答案是用 a * b / ab最大公约数。
那么求a、b、c的最小公倍数怎么做?答案是用 a * bc最小公倍数 / (a、bc最小公倍数 的最大公约数)。
求最大公约数的函数是 __gcd(a, b);
代码如下
class Solution {
public:
int nthUglyNumber(int n, int a, int b, int c) {
int a_b = __gcd(a, b);
int b_c = __gcd(b, c);
int a_c = __gcd(a, c);
long ab = (long)a * b / a_b;
long bc = (long)b * c / b_c;
long ac = (long)a * c / a_c;
long abc = (long)a * bc / __gcd((long)a, bc);
int l = min(min(a, b), c);
int r = INT_MAX;
while (l < r) {
int mid = l + (r-l)/2;
int numA = mid /a;
int numB = mid / b;
int numC = mid / c;
int numAB = mid / ab;
int numAC = mid / ac;
int numBC = mid / bc;
int numABC = mid / abc;
if (numA + numB + numC - numAB - numBC - numAC + numABC >= n) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
};