一、高斯(分布)过程(随机过程)是什么?
| 一维高斯分布 | 多维高斯分布 | 无限维高斯分布 |
| 高斯网络 | 高斯过程 |
简单的说,就是一系列关于连续域(时间或空间)的随机变量的联合,而且针对每一个时间或是空间点上的随机变量都是服从高斯分布的。
举个例子:倘若你人生的每一个时刻看做一个随机变量,且都是满足高斯分布,那么你的人生就可以看做一个高斯过程,既有很多确定的东西,确定的是mean和kernel,如你的人生中你起点决定的你人生的大致范围,又有极大地不确定性,本质还是随机变量的整体,就像你可以凭借自身的努力改变很多东西,这就是属于你的高斯过程。
二、高斯过程有什么用?--->高斯过程回归
简单的说,由于它性质完美,计算简单,形式漂亮,所以可以被广泛应用在各种统计建模中,包括一些非线性的预测推断问题
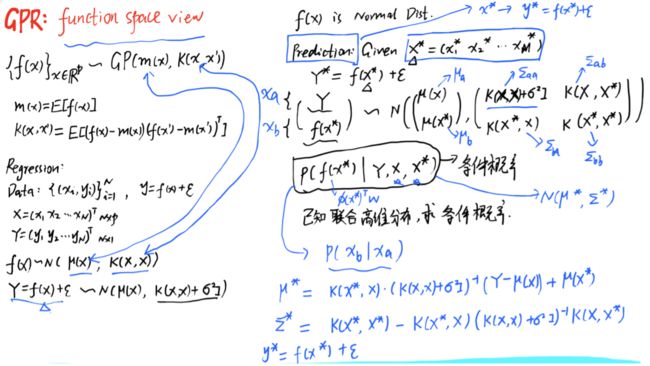
1、weight-space角度
先来回顾贝叶斯线性回归(Bayesian Linear Regression),分为两部分(1)Inference(2)预测
如果线性回归问题本身不是线性的,就要进行非线性转换,
2、weighted-space角度 ---> function-space 角度
3、function-space角度
三、高斯过程回归怎么用?
因为高斯分布在自然界无比常见,所以把原来的n个y看成服从高斯分布,来了一个新的Xn+1,这n+1个y还是服从一个联合正态分布的。
已知n个点的(xa,ya),想知道在任意一个新的点xb,对应的yb是怎么样的。可以用来进行贝叶斯优化。
其中,xa和xb,yb为观察到的值,ya为需要预测的值
要点:
1.简单来说,高斯过程可以看成是一个函数,函数的输入是x,函数的输出是高斯分布的均值和方差。
2.y的相关性取决于x,然后由x到y用高斯核函数表示其相关性
3.Y之间的分布用协方差矩阵表示
4、有噪声时把噪声加到对角线上
四、核函数如何选取?
对于上面的协方差矩阵K,其中k(x,y)表示核函数,那么这个核函数如选取?
1、高斯核函数
RBF(高斯核函数,也叫做径向基函数)
2、Matern核
参考文献:
【1】浅析高斯过程回归(Gaussian process regression)附代码
【2】高斯过程回归GPR
【3】浅谈高斯过程回归