计数排序（CountingSort）

一. 背景知识与目的
1、进行计数排序练习。
2、计数排序说明：
计数排序只适用于整数的排序。
3、实现原理：
1）假设整数带排序数组A[1..N]从0…K中的任意整数的数组。建立计数数组C[0…K],元素初始为0
2）然后计算A[j]元素值的个数，放在计数数组中，计算方法遍历A[1…N],C[A[j]]=C[A[j]]+1。
3)由于C[0…N]标识每个位置上的元素的个数，前一个元素加当前元素即为元素i的值的位置。相同元素占用相同位置，则计数减一依次输出。
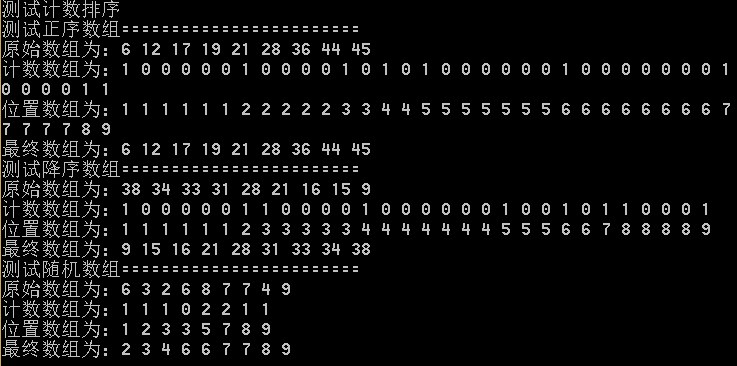
4）举例：
a)在0-5上的数组{1,3,1,2,4,0,2},C[0…5]={0,0,0,0,0,0}
b)C[A[0]]=C[A[0]]+1=1;C[A[2]]=C[A[2]]+1=2;即元素1存在两个元素。
C)计数数组为C[0…5]={1,2,2,1,1,0}
D)位置数组为C[0…5]={1,3,5,6,7,7},解释该数组，计数数组元素5对应计数为0，位置为7，依次不输出。元素4对应计数1，位置7，因此最后一个元素为4,只输出1次。依次3。元素2对应计数2，位置5，因此第4位第5位都为2…

二. 代码实现
实现代码

        //计数排序
        //计数排序只针对整数数组排序。
        void CountingSort(T testArray[], int nSize){
            LogInfo log = LogInfo();
            log.ShowState("原始数组为：");
            log.ShowArray(testArray, nSize);
            int k(0);
            //一次遍历获取最大值与最小值
            T TMax = testArray[0], TMin = testArray[0];
            for (int i = 0; i < nSize; i++){
                if (testArray[i]>TMax){
                    TMax = testArray[i];
                }
                else if (testArray[i] < TMin){
                    TMin = testArray[i];
                }
            }
            //定义数组的范围，K一般是最大值与最小值的差值，可以超过这个值。最小值默认为0
            k = TMax - TMin + 1;
            //初始化计数器
            T* Count = new int[k];
            for (int i = 0; i < k; i++)
                Count[i] = T(0);
            //计算每个计数器位置的元素个数
            for (int i = 0; i < nSize; i++){
                Count[testArray[i] - TMin] ++;
            }
            log.ShowState("计数数组为：");
            log.ShowArray(Count, k);
            //计算位置前置和
            for (int i = 1; i < k; i++)
                Count[i] = Count[i]+Count[i-1];
            log.ShowState("位置数组为：");
            log.ShowArray(Count, k);
            //定义输出数组
            T* testOut = new T[nSize];
            for (int i = nSize - 1; i >= 0; i--){
                testOut[Count[testArray[i] - TMin]-1] = testArray[i];
                Count[testArray[i] - TMin]--;
            }
            log.ShowState("最终数组为：");
            log.ShowArray(testOut, nSize);
            delete[] testOut, Count;
        }

调用代码

int main()
{
    using namespace Test;
    using namespace MyAlgorithm;
    using namespace std;

    LogInfo<int> log = LogInfo<int>();
    Sort<int> sortTest = Sort<int>();
    log.ShowState("测试计数排序");
    log.ShowLine();
    log.ShowState("测试正序数组========================");
    log.ShowLine();
    TestDataCreator<int, N_MAX> testArray = TestDataCreator<int, N_MAX>(PositiveArray);
    sortTest.CountingSort(testArray.GetArray(), testArray.GetSize());
    log.ShowState("测试降序数组========================");
    log.ShowLine();
    testArray = TestDataCreator<int, N_MAX>(NegativeArray);
    sortTest.CountingSort(testArray.GetArray(), testArray.GetSize());
    log.ShowState("测试随机数组========================");
    log.ShowLine();
    testArray = TestDataCreator<int, N_MAX>(RandomArray);
    sortTest.CountingSort(testArray.GetArray(), testArray.GetSize());
    int nWait;
    cin >> nWait;
    return 0;
}

结果输出

三. 遇到问题
1、需要输出计数数组与位置数组因此Count定义为T*
2、由于位置从1开始，因此放在数组中需要-1
3、无法确定K值，因此一次遍历获取最大值与最小值。
四. 经验总结
1、计数排序算法稳定。空间复杂度O(N+K),时间复杂度为O(N+K)，对于本例时间复杂度为O(2*N+K)
2、计数排序不用比较元素的大小，基于位置计数。是一种线性复杂度的排序算法。
3、最坏情况下，任何比较排序复杂度都至少需要Nlog2(N)次比较。
五. 后续计划
1、进行基数排序与桶排序练习。

六. 参考文献
1、算法导论
2、 八大排序算法 http://blog.csdn.net/abcbig/article/details/42774333
3、计数排序http://www.cnblogs.com/kaituorensheng/archive/2013/02/23/2923877.html