瓶颈
如何理解树状数组?
这个结构的思想和线段树有些类似:用一个大节点表示一些小节点的信息,进行查询的时候只需要查询一些大节点而不是更多的小节点。
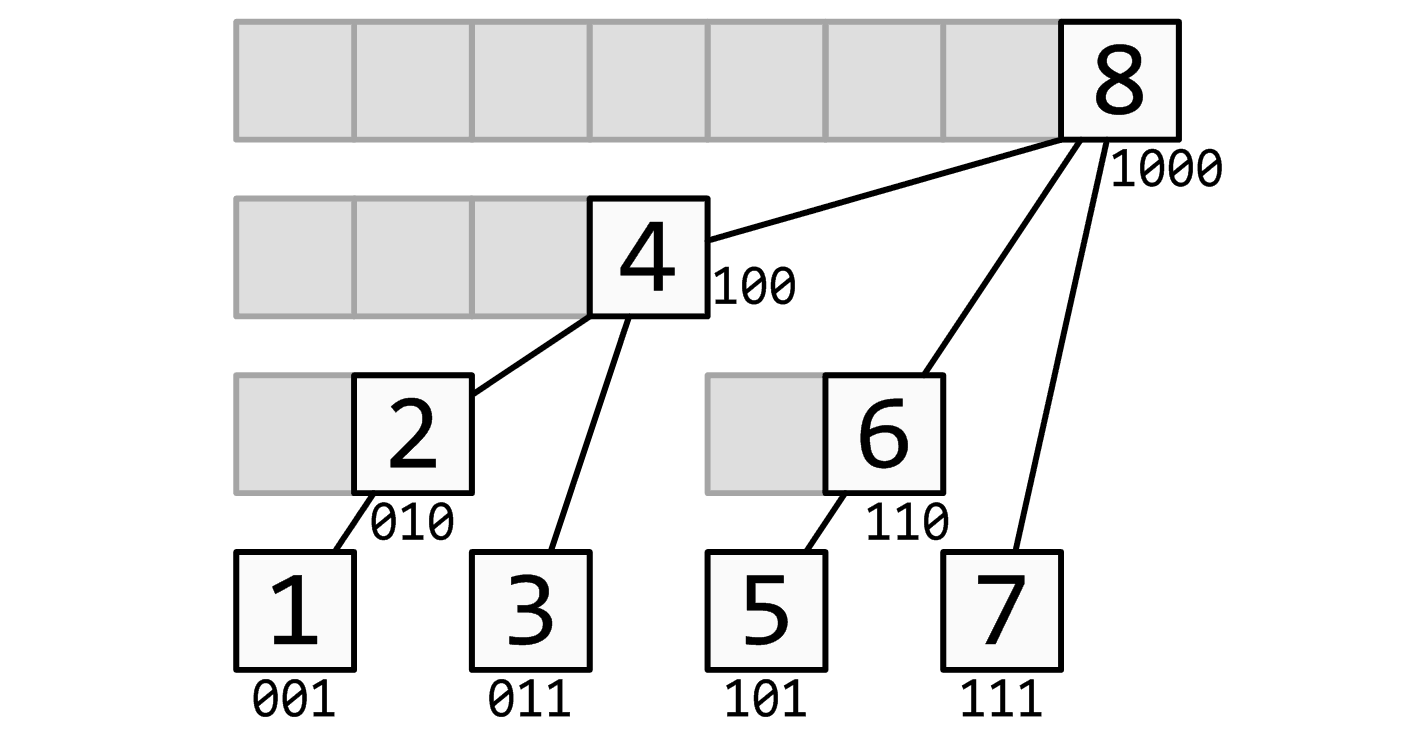
最下面的八个方块就代表存入 a 中的八个数,现在都是十进制。
他们上面的参差不齐的剩下的方块就代表 a 的上级—— c 数组。
很显然看出: c2 管理的是 a1 & a2 ; c4 管理的是 a1 & a2 & a3 & a4 ; c6 管理的是 a5 & a6 ;c8 则管理全部 8 个数。
所以,如果你要算区间和的话,比如说要算 a51 ~ a91 的区间和,暴力算当然可以,那上百万的数,那就 TLE 喽。
——————摘自oi-wiki.org
初看这些文字,你可能会想:
“啊这这这???你讲这些我们怎么听得懂啊,这树状数组是啥,咋用,我们还是懵的啊”
当然,为了解决问题而书写算法的话,我们不需要去理解这个结构的原理到底是啥,我们只需要知道这个东西
用在哪?
怎么用?
就足够了
用在哪?
我们都知道:
一般的普通数组单点操作的时间复杂度的O(1)、区间操作的时间复杂度是O(n)。
而我们树状数组的和普通数组的区别就在于:
单点操作和区间操作的时间复杂度都是O(log n),而且
单点修改和区间操作(加、求和)都需要用函数实现。
那么这么说我们大概能理解一点了,那就是:
一旦遇到大规模使用区间求和的问题,我们就可以考虑使用树状数组。
怎么用?
总得来说就是三个函数:lowbit、添加函数,求和函数
lowbit
int lowbit(int x) {
/*
算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数
简单说就是用位运算改变了查找操作,以契合上述的时间复杂度
*/
return x & -x;
}
单点修改
void add(int x, int k) { //在i位置加上k
while (x <= n) { // 不能越界
c[x] = c[x] + k;
x = x + lowbit(x);
}
}
区间求和
int sum(int x) { // 返回a[1]……a[x]的和
int ans = 0;
while (x >= 1) {
ans = ans + c[x];
x = x - lowbit(x);
}
return ans;
}
就这??就这??
啊啊,看似就这,那我们来找一道模板题做一做,深化一下理解吧。
例题:Acwing 788 逆序对的数量
题面
给定一个长度为n的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对;否则不是。
输入
第一行包含整数n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出
输出一个整数,表示逆序对的个数。
PS: 1≤n≤1000001≤n≤100000
输入样例:
6
2 3 4 5 6 1
输出样例:
5
解题过程
“逆序对”的计算需要用到大量的区间运算,在这个时候我们的树状数组就发挥了很大的用处了,
对于这道题的核心思想,即是:
用数组的值作为下标,每次出现逆序对则给该下标对应值加一,最后求和
代码如下
#include#include #include #include using namespace std; typedef long long LL; const int N = 100010; int n; int a[N]; int tr[N]; int lowbit(int x) { return x & -x; } void add(int x, int k) { for (int i = x; i < N - 1; i += lowbit(i)) tr[i] += k; } LL sum(int x) { LL res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } int main() { scanf("%d", &n); for (int i = 0; i < n; i ++) scanf("%d", &a[i]); LL ans = 0; for (int i = n - 1; i >= 0; i --) {//倒序读入 int t = a[i];//读入的值作为下标 ans += sum(t - 1);//若比a[i]小的值在其之前被读入,即出现了逆序对 add(t, 1);//记录逆序对 } printf("%lld\n", ans); return 0; }
emmm,样例过了,提交!
诶怎么wa了,还是段错误?
看了看测试数据,原来是我们将数据当作下标,而数据的大小超过了数组大小的限制,而且也造成了空间的冗余,这个时候,我们想到一个方法:
离散化
离散化,即是将对象之间的关系模糊化,在不改变数据相对大小的条件下,对数据进行相应的缩小。
什么意思呢?
比如说:
在{ 1、 2、 99999、 3 }之间判断逆序对和在{ 1、 2、 4、 3}之间判断逆序对在基本流程上无差别,而如果不进行离散化,则花费了99999个空间,为了节省空间,也为了消除数组越界的风险,我们使用离散化优化一下代码。
#include#include #include #include using namespace std; typedef long long LL; const int N = 100010; int n; int a[N], backup[N];//backup即是离散化之后的序列 LL tr[N]; int lowbit(int x) { return x & -x; } void add(int x, int k) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += k; } LL sum(int x) { LL res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } int find(int k) {//查找(利用了二分的思想) int l = 0, r = n - 1; while (l < r) { int mid = l + r + 1 >> 1; if (backup[mid] <= k) l = mid; else r = mid - 1; } return r + 1; } //排好序存储进来的序列,其每个元素的对应下标就是其离散化之后的“大小” int main() { scanf("%d", &n); for (int i = 0; i < n; i ++) scanf("%d", &a[i]); memcpy(backup, a, sizeof a); sort(backup, backup + n);//进行排序 LL ans = 0; for (int i = n - 1; i >= 0; i --) { int t = find(a[i]); ans += sum(t - 1); add(t, 1); } printf("%lld\n", ans); return 0; }
最后,我们得到了AC!!!
希望我的抛砖引玉能引起更多的思考! (蒟蒻鞠躬)。