Love_marginal

[文献提炼] 车联网中资源分配的问题建模又三篇

前言

摘录和分析看过的论文中 SYSTEM MODEL / PROBLEM FORMULATION 的部分，关注论文的关键词为 UUDN V2X RL。

本文为第二期，第一期链接：https://blog.csdn.net/m0_37495408/article/details/107546431

Model-Free Ultra Reliable Low Latency Communication (URLLC): a Deep Reinforcement Learning Framework

这是一个2019年来自ICC的文章

链路的表示：考虑单一基站覆盖下的场景，其中存在N个用户和K个可用的RB。每个用户有其独立的速率、可靠性、延迟需求。本文不对包到达及包长度做任何假设。

下行传输速率为：

$\LARGE r_{i}(t)=\sum_{j=1}^{K} \rho_{i j}(t) B \log _{2}\left(1+\frac{p_{i j}(t) h_{i j}(t)}{\sigma^{2}}\right)$

其中B为带宽，h为时变的 V2I 瑞丽衰落信道增益，p 为下行传输功率， $\LARGE \rho$ 为RB分配。

可靠性表示：可靠性 $\LARGE \gamma_i(t)$ 定义其为时延超过预定义阈值 $\LARGE D_i^{max}$ 的概率，时延分成传输时延和排队时延两部分。

传输速率约束于包尺寸、包到达率、可靠性： $\LARGE r_{i}(t)>\phi\left(\lambda_{i}(t), \beta(t), \gamma_{i}, D_{i}^{\max }\right)>\lambda_{i}(t) \beta_{i}(t)$

其中 $\LARGE \beta$ 是包尺寸、 $\LARGE \lambda$ 是包的平均到达速率、 $\LARGE \phi$ 表征传输速率和速率、包到达率、可靠性的一个映射（函数）。

目标是在保证可靠性、延迟、速率的前提下最小化BS的平均下行功率：

约束于

3b：用包延迟描述的可靠性约束（D_i是i号用户的包延迟）
3c、3d：可行性条件

整个资源分配分两个步骤：1.根据可靠性决定每个用户的传输速率；2.分配功率和RB到每个用户。

根据排队论可得3b中的可靠性为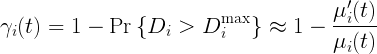： $\LARGE \gamma_{i}(t)=1-\operatorname{Pr}\left\{D_{i}>D_{i}^{\max }\right\} \approx 1-\frac{\mu_{i}^{\prime}(t)}{\mu_{i}(t)}$ ， $\LARGE \mu'$ 是用户i 在slot内延迟超限的包的数量， $\LARGE \mu$ 是用户在slot内传输的包的总数量。当\mu增大，上式将近似收敛于 (3b) 中的可靠性。

Learn to Compress CSI and Allocate Resources in Vehicular Networks

2020年来自 IEEE TRANSACTIONS ON COMMUNICATIONS 的文章

链路表示：考虑一个有N个蜂窝用户、K对D2D链路、单一BS覆盖下的车联网，D2D交换安全信息，蜂窝用户使用V2I来支持大流量的应用。为保证蜂窝用户的QoS，假设V2I使用正交的频谱资源，并且其上行传输时仅占用一个信道。V2V与V2I分享频谱。

V2I的SINR的表示： $\LARGE \gamma_{n}^{c}[n]=\frac{P_{n}^{c} g_{n}[n]}{\sum_{k=1}^{K} \rho_{k}[n] P_{k}^{d} h_{k, B}[n]+\sigma^{2}}$ ，其中g[n]为CU(蜂窝用户)在n号信道到基站的信道增益，h为来自k号V2V的干扰，P为发射功率， $\LARGE \sigma^2$ 表示噪声功率， $\LARGE \rho$ 表示信道分配。我们假设每个D2D对进展用一个信道。

V2I信道容量的表示： $\LARGE C_{n}^{c}[n]=B \log _{2}\left(1+\gamma_{n}^{c}[n]\right)$ ，B为信道带宽。

V2V链路的SINR和信道容量的计算类似： $\LARGE \gamma_{k}^{d}[n]=\frac{\rho_{k}[n] P_{k}^{d} h_{k}[n]}{I_{k}[n]+\sigma^{2}}$ ， $\LARGE I_{k}[n]=\sum_{l \neq k}^{K} \rho_{l}[n] P_{l}^{d} h_{l, k}[n]+P_{n}^{c} g_{n, k}[n]$

$\LARGE C_{k}^{d}[n]=B \log _{2}\left(1+\gamma_{k}^{d}[n]\right)$

奖励设计： $\LARGE R=\lambda_{c} \sum_{n=1}^{N} C_{n}^{c}[n]+\lambda_{d} \sum_{k=1}^{K} C_{k}^{d}$ ，两项分别表示V2I和V2V的信道容量

自变量： $\LARGE a = \{\rho_1, ...,\rho_k, ...,\rho_K \}$ 表示对于 k号V2V链路的信道分配向量。

Intelligent Resource Management Based on Reinforcement Learning for Ultra-Reliable and Low-Latency IoV Communication Networks

链路的表示：场景中存在K个蜂窝用户，M个 D2D-V2V 对，使用OFDMA (正交频分多址)以服务多个UE，考虑上行链路，存在N (>K) 个正交的RB，假设每个蜂窝用户只能占用一个RB，并且该RB最多被D2D重用一次。

SINR的表示： $\LARGE h_k ,h_m$ 分别表示蜂窝用户和D2D对的信道增益， $\LARGE g_{k, m}, g_{k, m, B}$ 分别表示蜂窝用户与D2D对之间的干扰、D2D对对BS在k号RB上的干扰。假设上述的量都是由PL，大尺小尺构成的。

D2D对有三种模式可以选择：

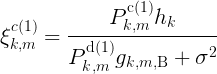
重用模式：D2D对可以使用蜂窝用户占用的RB，此时k号蜂窝用户的SINR为： $\LARGE \xi_{k, m}^{c(1)}=\frac{P_{k, m}^{\mathrm{c}(1)} h_{k}}{P_{k, m}^{\mathrm{d}(1)} g_{k, m, \mathrm{B}}+\sigma^{2}}$
分子的 $\LARGE \sigma^2$ 为噪声功率，并且我们蜂窝用户的噪声功率都相等。
D2D对的上行SINR为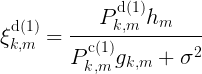： $\LARGE \xi_{k, m}^{\mathrm{d}(1)}=\frac{P_{k, m}^{\mathrm{d}(1)} h_{m}}{P_{k, m}^{\mathrm{c}(1)} g_{k, m}+\sigma^{2}}$
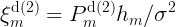
专用模式：一个RB块仅分配给一个D2D对，此时D2D对的上行SINR为： $\LARGE \xi_{m}^{\mathrm{d}(2)}=P_{m}^{\mathrm{d}(2)} h_{m} / \sigma^{2}$
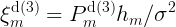蜂窝模式（用蜂窝作中继）：当D2D对相距过远时，可以使用BS做中继。此时每个UE视作一个普通的蜂窝用户，其各自占用一个RB，此RB规定不被别人使用。所以D2D对的SINR为： $\LARGE \xi_{m}^{\mathrm{d}(3)}=P_{m}^{\mathrm{d}(3)} h_{m} / \sigma^{2}$ 。

一般来讲，当蜂窝用户的RB没有被重用时，其上行SINR为 $\LARGE \xi_{k}^{\mathrm{c}(2)}=P_{k}^{\mathrm{c}(2)} h_{k} / \sigma^{2}$

蜂窝用户的总数据率：

$\LARGE \begin{aligned} R_{k}^{\mathrm{c}}=& x_{k, m}^{\mathrm{d}(1)} \log _{2}\left(1+\xi_{k, m}^{\mathrm{c}(1)}\right) \\ &+\left(1-\sum_{m \in \mathcal{M}} x_{k, m}^{\mathrm{d}(1)}\right) \log _{2}\left(1+\xi_{k}^{\mathrm{c}(2)}\right) \end{aligned}$

D2D链路的总数据率：

$\LARGE \begin{aligned} R_{m}^{\mathrm{d}}=& \sum_{k \in \mathcal{K}}\left(x_{k, m}^{\mathrm{d}(1)} \log _{2}\left(1+\xi_{k, m}^{\mathrm{d}(1)}\right)\right) \\ &+x_{m}^{\mathrm{d}(2)} \log _{2}\left(1+\xi_{m}^{\mathrm{d}(2)}\right)+x_{m}^{\mathrm{d}(3)} \log _{2}\left(1+\xi_{m}^{\mathrm{d}(3)}\right) \end{aligned}$

约束构建：通信服务分作两个场景：1.单播场景（传递交通安全类信息，对URLLC要求严格但对数据率要求宽松）；2.普通场景（要求大数据速率）。

普通场景下的最小数据速率约束： $\LARGE R_{k}^{\mathrm{c}} \geq R_{k}^{\mathrm{c}, \mathrm{tar}}, \forall k, \text { and }, R_{m}^{\mathrm{d}, \mathrm{nor}} \geq R_{m}^{\mathrm{d}, \mathrm{nor}, \mathrm{tar}}, \forall m$ ，其中 $\LARGE d^{d, nor}_m$ 表示通常场景下D2D对的数据率，加上tar角标的是最小数据率阈值。

传输延迟的表示： $\LARGE T_{tx} = \tau_{mac}+\tau_{data}$ ，前者时物理层三次握手的时延、后者是数据传输时延。

对于单播场景下的D2D链路，其延迟约束为： $\LARGE p_{m}^{\mathrm{dclay}}=\operatorname{Pr}\left\{T_{\mathrm{tx}} \geq T_{\max }\right\} \leq p_{\max }^{\mathrm{delay}}$

可靠性约束为： $\LARGE p_{m}^{\text {outage }}=\operatorname{Pr}\left\{R_{m}^{\mathrm{d}, \mathrm{uni}} \leq R_{m}^{\mathrm{d}, \mathrm{uni}, \operatorname{tar}}\right\} \leq p_{\max }^{\text {outage }}$

问题构建：

$\LARGE \begin{array}{l} \max _{\mathbf{x}, \mathbf{P}}\left\{\sum_{k \in \mathcal{K}} R_{k}^{\mathrm{c}}+\sum_{m \in \mathcal{M}_{\mathrm{nor}}} R_{m}^{\mathrm{d}, \mathrm{nor}}\right\} \\ \text { s.t. }(8),(9),(10) ; x_{k, m}^{\mathrm{d}(1)}, x_{m}^{\mathrm{d}(2)}, x_{m}^{\mathrm{d}(3)} \in\{0,1\}, \forall m \end{array}$

$\LARGE \begin{array}{l} \sum_{m \in \mathcal{M}} x_{k, m}^{\mathrm{d}(1)} \leq 1, \forall k \\ \sum_{k \in \mathcal{K}} x_{k, m}^{\mathrm{d}(1)}+x_{m}^{\mathrm{d}(2)}+x_{m}^{\mathrm{d}(3)} \leq 1, \forall k \\ \sum_{m \in \mathcal{M}} x_{m}^{\mathrm{d}(2)}+\sum_{m \in \mathcal{M}} x_{m}^{\mathrm{d}(3)} \leq N_{\mathrm{U}} \\ \sum_{k \in \mathcal{K}}\left(x_{k, m}^{\mathrm{d}(1)} P_{k, m}^{\mathrm{d}(1)}\right)+x_{m}^{\mathrm{d}(2)} P_{m}^{\mathrm{d}(2)} \\ \quad+x_{m}^{\mathrm{d}(3)} P_{m}^{\mathrm{d}(3)} \leq P_{\max }^{\mathrm{d}}, \forall m \\ x_{k, m}^{\mathrm{d}(1)} P_{k, m}^{\mathrm{c}(1)}+\left(1-\sum_{m \in \mathcal{M}} x_{k, m}^{\mathrm{d}(1)}\right) P_{k}^{\mathrm{c}(2)} \leq P_{\max }^{\mathrm{c}}, \forall k \end{array}$

其中 $\LARGE x = \{x^{(1)},x^{(2)},x^{(3)}\}$ 表征模式选择和RB分配，P表示发射功率矩阵， $\LARGE M_{nor}$ 表示通常场景下的D2D对。

奖励函数：

$\LARGE $\begin{aligned} r=& c_{1}\left(\sum_{k \in \mathcal{K}} R_{k}^{\mathrm{c}}+\sum_{m \in \mathcal{M}_{\mathrm{nor}}} R_{m}^{\mathrm{d}, \mathrm{nor}}\right) \\ &-c_{2}\left(\sum_{m\in\mathcal{M}_{uni}}(p_m^{delay}+p_m^{outage})\right) \\ &-c_{3}\left(\sum_{k\in\mathcal{M}_{\mathrm{uni}}}\left(R_{k}^{c,tar}+R_{k}^{c}\right)+\sum_{m\in\mathcal{M}_{nor}}(R_m^{d, nor,tar}-R_m^{d,nor}))\right) \end{aligned}$$

动作空间构建： $\LARGE $a=\left\{\beta_{\mathrm{ms}}, \beta_{\mathrm{rb}}, \beta_{\mathrm{po}}\right\}$$ 通信模式选择、RB分配决策、功率等级选择。(动作选择需要满足原优化问题的约束)

总结

论文	论文1	论文2	论文3
资源分配的对象	传输速率用户的功率和RB分配	$\LARGE a = \{\rho_1, ...,\rho_k, ...,\rho_K \}$ 表示对于 k号V2V链路的信道分配向量	通信模式选择、RB分配决策、功率等级选择。(动作选择需要满足原优化问题的约束)
优化目标	$\LARGE \min _{p_{i j}, \rho_{i j}} \lim _{t \rightarrow \infty} \frac{1}{t} \sum_{\tau=1}^{t} \sum_{i=1}^{N} \sum_{j=1}^{K} p_{i j}(\tau)$	$\LARGE R=\lambda_{c} \sum_{n=1}^{N} C_{n}^{c}[n]+\lambda_{d} \sum_{k=1}^{K} C_{k}^{d}$	$\LARGE $\begin{aligned} r=& c_{1}\left(\sum_{k \in \mathcal{K}} R_{k}^{\mathrm{c}}+\sum_{m \in \mathcal{M}_{\mathrm{nor}}} R_{m}^{\mathrm{d}, \mathrm{nor}}\right) \\ &-c_{2}\left(\sum_{m\in\mathcal{M}_{uni}}(p_m^{delay}+p_m^{outage})\right) \\ &-c_{3}\left(\sum_{k\in\mathcal{M}_{\mathrm{uni}}}\left(R_{k}^{c,tar}+R_{k}^{c}\right)+\sum_{m\in\mathcal{M}_{nor}}(R_m^{d, nor,tar}-R_m^{d,nor}))\right) \end{aligned}$$
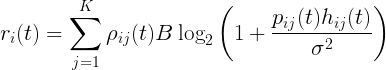信道容量	$\LARGE r_{i}(t)=\sum_{j=1}^{K} \rho_{i j}(t) B \log _{2}\left(1+\frac{p_{i j}(t) h_{i j}(t)}{\sigma^{2}}\right)$	V2I $\LARGE \gamma_{n}^{c}[n]=\frac{P_{n}^{c} g_{n}[n]}{\sum_{k=1}^{K} \rho_{k}[n] P_{k}^{d} h_{k, B}[n]+\sigma^{2}}$ $\LARGE C_{n}^{c}[n]=B \log _{2}\left(1+\gamma_{n}^{c}[n]\right)$ V2V $\LARGE \gamma_{k}^{d}[n]=\frac{\rho_{k}[n] P_{k}^{d} h_{k}[n]}{I_{k}[n]+\sigma^{2}}$ ， $\LARGE I_{k}[n]=\sum_{l \neq k}^{K} \rho_{l}[n] P_{l}^{d} h_{l, k}[n]+P_{n}^{c} g_{n, k}[n]$ $\LARGE C_{k}^{d}[n]=B \log _{2}\left(1+\gamma_{k}^{d}[n]\right)$	蜂窝： $\LARGE \begin{aligned} R_{k}^{\mathrm{c}}=& x_{k, m}^{\mathrm{d}(1)} \log _{2}\left(1+\xi_{k, m}^{\mathrm{c}(1)}\right) \\ &+\left(1-\sum_{m \in \mathcal{M}} x_{k, m}^{\mathrm{d}(1)}\right) \log _{2}\left(1+\xi_{k}^{\mathrm{c}(2)}\right) \end{aligned}$ D2D： $\LARGE \begin{aligned} R_{m}^{\mathrm{d}}=& \sum_{k \in \mathcal{K}}\left(x_{k, m}^{\mathrm{d}(1)} \log _{2}\left(1+\xi_{k, m}^{\mathrm{d}(1)}\right)\right) \\ &+x_{m}^{\mathrm{d}(2)} \log _{2}\left(1+\xi_{m}^{\mathrm{d}(2)}\right)+x_{m}^{\mathrm{d}(3)} \log _{2}\left(1+\xi_{m}^{\mathrm{d}(3)}\right) \end{aligned}$
约束	$\LARGE \begin{array}{l} \operatorname{Pr}\left\{D_{i}>D_{i}^{\max }\right\}<1-\gamma_{i}^{*}, \quad \forall i \in \mathcal{N} \\ p_{i j}(t) \geq 0, \quad \rho_{i j}(t) \in\{0,1\} \\ \forall i \in \mathcal{N}, \quad \forall j \in \mathcal{K}, \quad \forall t (3c))\\ \sum_{i} \rho_{i j}(t)=1, \quad \forall j \in \mathcal{K}, \quad \forall t \end{array}$ 3b：用包延迟描述的可靠性约束（D_i是i号用户的包延迟） 3c、3d：可行性条件		通常场景： $\LARGE R_{k}^{\mathrm{c}} \geq R_{k}^{\mathrm{c}, \mathrm{tar}}, \forall k, \text { and }, R_{m}^{\mathrm{d}, \mathrm{nor}} \geq R_{m}^{\mathrm{d}, \mathrm{nor}, \mathrm{tar}}, \forall m$

【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
Hadoop 傲雪凌霜，松柏长青后端大数据 hadoop 大数据分布式
ApacheHadoop是一个开源的分布式计算框架，主要用于处理海量数据集。它具有高度的可扩展性、容错性和高效的分布式存储与计算能力。Hadoop核心由四个主要模块组成，分别是HDFS（分布式文件系统）、MapReduce（分布式计算框架）、YARN（资源管理）和HadoopCommon（公共工具和库）。1.HDFS（HadoopDistributedFileSystem）HDFS是Hadoop生
二十四、k8s 资源管理繁华依在 k8s kubernetes 容器云原生
目录一、资源配置范围管理LimitRange介绍1、LimitRange可以做什么：2、资源限制和请求的约束3、创建LimitsRange对象4、示例：创建一个pod5、测试用例测试1：测试2：测试3：二、资源服务质量管理（RequestsQos）1、Qos级别分类：1.1、Guaranteed：1.2、BestEffort：1.3、Burstable：2、Qos的工作特点3、示例三、资源配额管理
埃隆·马斯克表示特斯拉“没有必要”授权 xAI 模型喜好儿网人工智能 AIGC 马斯克
埃隆·马斯克近日在社交媒体上对《华尔街日报》的一篇报道进行了反驳。该报道指出，马斯克旗下的电动汽车公司特斯拉可能与人工智能初创公司xAI达成了一项收入分享协议，以便特斯拉能够使用xAI的人工智能模型。据称，这些模型将被集成到特斯拉的全自动驾驶（FSD）软件中，并可能用于开发特斯拉汽车的语音助手以及人形机器人擎天柱的软件。喜好儿网然而，马斯克否认了这一说法，他在社交媒体平台上表示，尽管特斯拉确实与x
（k8s）Kubernetes 从0到1容器编排之旅道不贱卖，法不轻传 kubernets kubernetes 容器云原生
一、引言在当今数字化的浪潮中，Kubernetes如同一艘强大的航船，引领着容器化应用的部署与管理。它以其卓越的灵活性、可扩展性和可靠性，成为众多企业和开发者的首选。然而，要真正发挥Kubernetes的强大威力，仅仅掌握基本操作是远远不够的。本文将带你深入探索Kubernetes使用过程中的奇技妙法，为你开启一段优雅的容器编排之旅。二、高级资源管理之精妙艺术1.资源配额与限制：雕琢资源之美•Ku
2022-03-01 薇薇林
为什么企业人力资源管理师证书没有用？人力资源管理，俗称HR，是个人就能做吗？在普罗大众的刻板印象里，HR人事就是招招人，发发工资，五点准时下班，闲得很，技术门槛为零。但人力资源管理是包含了六大模块的，说人话就是会定KPI、会做培训体系，上能在招聘宣传中娓娓道来，下能狠心开除问题员工，对内可甜，对外可盐。优秀的大公司都把人力看做第一资源。在汇丰银行，HR是有一票否决权的，即使你通过部门主管的面试、部
详解 Flink 的常见部署方式文刀小桂 Flink flink 大数据
一、常见部署模式分类1.按是否依赖外部资源调度1.1Standalone模式独立模式(Standalone)是独立运行的，不依赖任何外部的资源管理平台，只需要运行所有Flink组件服务1.2Yarn模式Yarn模式是指客户端把Flink应用提交给Yarn的ResourceManager,Yarn的ResourceManager会在Yarn的NodeManager上创建容器。在这些容器上，Flink
Microsoft Defender SmartScreen 阻止了无法识别的应用启动。运行此应用可能会导致你的电脑存在风险。开心呆哥 microsoft
你提到的情况可能是由于Windows的安全策略导致的。当你运行批处理文件（.bat）时，Windows可能会弹出一次提示，询问是否允许该文件执行。这是为了确保用户不会意外地运行潜在的恶意脚本。有几种方法可以解决这个问题：解锁文件：在文件资源管理器中，找到你的.bat文件。右键单击文件，选择"属性"。在"常规"选项卡中，如果有一个"解锁"复选框，请勾选它。确定并尝试重新运行文件。以管理员身份运行：右
边缘计算在现代数据中心的应用 666IDCaaa 边缘计算人工智能
当今数字化时代，数据中心扮演着至关重要的角色，而边缘计算的出现为现代数据中心带来了新的机遇和挑战。一、边缘计算的概念与特点边缘计算是一种将计算和数据存储靠近数据源或用户的分布式计算模式。与传统的集中式云计算相比，边缘计算具有以下特点：低延迟：由于数据处理在靠近数据源的地方进行，减少了数据传输的距离和时间，从而实现了更低的延迟。这对于实时性要求高的应用，如工业自动化、自动驾驶、虚拟现实等至关重要。高
一切皆是映射：AI的去中心化：区块链技术的融合 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
一切皆是映射：AI的去中心化：区块链技术的融合作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming关键词：AI，区块链，去中心化，智能合约，共识机制，数据安全，隐私保护，分布式账本技术，机器学习，数据隐私1.背景介绍1.1问题的由来随着人工智能（AI）技术的快速发展，其在各个领域的应用越来越广泛，从自动驾驶、智能医疗到金融服务，AI正在改变着我们的生活。
操作sqlserver 抛出异常 CMemoryException weixin_30484247 数据库
恭喜一下自己，还在内存中打转；并且短时间出不来了。说打开sqlserver就发现内存一直涨没有停下来的势头，怀疑是sqlserver有内存泄露——其实这是sqlserver的机制，只要内存不大于设定的最大内存，sqlserver就不释放。那么为什么会出现CMemoryException？打开资源管理器，注意到此时sqlserver占1.6G，远程管理占700M，windows自身占1G，本身的数据
[C++11] 移动语意和移动构造函数图王大胜计算机学科基础开发语言 c++移动语意移动构造函数
说明：移动语义（MoveSemantics）是C++11引入的一个重要概念，旨在提高大型对象（特别是那些涉及资源管理的对象）的复制效率。移动语义允许资源从一个对象“移动”到另一个对象，而不是进行昂贵的复制操作。这种机制通过右值引用（right-valuereference）和移动构造函数（moveconstructor）以及移动赋值操作符（moveassignmentoperator）来实现。而移
深入解析Java的四种引用 Y雨何时停T Java java
引言：为什么需要理解Java的引用类型？在Java中，对象的管理是通过引用来实现的。垃圾回收器（GarbageCollector，简称GC）自动管理内存，但有时候我们希望更精细地控制对象的生命周期，这就引出了不同类型的引用：强引用、软引用、弱引用和虚引用。通过这些引用类型，开发者可以在内存敏感的场景中优化应用程序的性能和资源管理。Java中的四种引用类型Java中的引用类型定义在java.lang
快捷方式指向的驱动器或网络连接不可用元凌丶 windows
由于电脑固态硬盘有问题换了个盘，数据丢失了有些软件就暂时存到了C盘。装回来之后发现任务栏的快捷方式图标显示不正确。有相关解决办法是说把【appdata】路径下的【Iconcache.db】删除然后让Windows资源管理器重启。但是这种方法有和我情况相似的同学可能解决不了。需要把快捷方式的目标路径改一下。（我只解决了自己的问题，不确定是否一样，大家举一反三应该可以找到）1，首先要找到丢失图标的快捷
【ShuQiHere】探索人工智能核心：机器学习的奥秘 ShuQiHere 人工智能机器学习
【ShuQiHere】什么是机器学习？机器学习（MachineLearning,ML）是人工智能（ArtificialIntelligence,AI）中最关键的组成部分之一。它使得计算机不仅能够处理数据，还能从数据中学习，从而做出预测和决策。无论是语音识别、自动驾驶还是推荐系统，背后都依赖于机器学习模型。机器学习与传统的编程不同，它不再依赖于人类编写的固定规则，而是通过数据自我改进模型，从而更灵活
端到端的自动驾驶论文与代码整理大别山伧父自动驾驶
LearningbyCheatinggithubcodearxivpaperconferenceonrobotlearning最新进展(May2021)Checkoutourlatestfollow-upwork:WorldonRails(2020)Checkoutoursubmissiontothe2020CARLAChallenge!pass
机器学习与深度学习的区别 eqa11 机器学习
文章目录机器学习与深度学习的区别一、引言二、机器学习概述1、机器学习定义1.1、机器学习的应用2、机器学习算法三、深度学习概述1、深度学习定义1.1、深度学习的应用2、深度学习算法四、机器学习与深度学习的区别1、学习方法2、数据需求3、应用领域五、总结机器学习与深度学习的区别一、引言在人工智能的浪潮中，机器学习和深度学习无疑是最耀眼的两颗明星。它们在许多领域都取得了令人瞩目的成就，从自动驾驶汽车到
使用c++编写com组件实现windows外壳扩展（自定义右键上下文菜单扩展）小码ssim c++windows 开发语言
一、作用允许在Windows文件资源管理器中，当用户在文件、文件夹或空白处右键点击时，根据一定的逻辑显示自定义的菜单项二、原理COM组件微软开发的一种软件架构模型，主要用于在不同编程语言之间实现二进制级别的可重用性和互操作性。它可以作为独立的模块分发，并能够在应用程序之间共享，广泛应用于Windows操作系统中的许多服务和应用程序中。（C++和C#是开发COM组件的主要语言。C++提供了最直接的访
陈茹-中原焦点团队讲师6期坚持分享第912天20210304 陈妍羽2018
珍惜生命最好的办法是管理情绪(2)我们一直低估了身体的智慧人体里有着一套精密的免疫系统我这里说的免疫系统，不仅是西医所说的狭义的免疫能力，还包含自我诊断、人体资源管理、自我修复及再生。当我们产生各种各样的情绪的时候，最先被攻击到的是身体的免疫系统。70％以上的人会以攻击自己身体器官的方式来消化自己的情绪，这是导致出现病症的最大原因之一。不同情绪会攻击不同的器官，我国中医的古老智慧就曾提出：肾主恐惧
GaN HEMT：未来功率半导体 David WangYang 硬件工程
硅基金属氧化物自1960年代以来，硅基金属氧化物半导体场效应晶体管（MOSFET）一直是电力电子应用的标准。尽管如此，各种技术的发展（尤其是在汽车和消费电子领域）给寻求以越来越小的外形尺寸提供更高效率和更大功率密度的开发人员带来了新的挑战。从大型数据中心和墙壁插座交流适配器到汽车车载充电站，各种用途的电源都需要高电压，同时尽可能少地占用宝贵的电路板空间。自动驾驶汽车还需要更高效的能量分配，以运行越
Python编码系列—Python团队开发工作流：高效协作的艺术学步_技术 Python编码 python 团队开发开发语言
欢迎来到我的技术小筑，一个专为技术探索者打造的交流空间。在这里，我们不仅分享代码的智慧，还探讨技术的深度与广度。无论您是资深开发者还是技术新手，这里都有一片属于您的天空。让我们在知识的海洋中一起航行，共同成长，探索技术的无限可能。探索专栏：学步_技术的首页——持续学习，不断进步，让学习成为我们共同的习惯，让总结成为我们前进的动力。技术导航：人工智能：深入探讨人工智能领域核心技术。自动驾驶：分享自动
大模型实战—Ollama 本地部署大模型猫猫姐大模型大模型
Ollama本地部署大模型在当今的科技时代，AI已经成为许多领域的关键技术。AI的应用范围广泛，从自动驾驶汽车到语音助手，再到智能家居系统，都有着AI的身影，而随着Facebook开源LLama2更让越来越多的人接触到了开源大模型。今天我们推荐的是一条命令快速在本地运行大模型，在GitHub超过22KStar的开源项目：ollama随着围绕着Ollama的生态走向前台，更多用户也可以方便地在自己电
以人力资源管理理论为切入点分析杨甦宏三分法汉塞哥
1.大学课堂存在问题大学课程是我们本科专业人才培养的基础，每一个优秀大学在其发展的征途中无不留下独特的追求卓越的课程哲学脚印。大学的核心内容就是大学课堂，然而，细致考查当下的国内大学课程，我们却不得不经常面对我国大学课程建设落后的尴尬。比如，一段时间以来不少高校开设的通识课程和专业课程却屡屡沦落为“水课”，有关单位在调查中发现大约有80%同学上课时光是在手机和睡梦中渡过来。这种常态也不断地刺激我们
五款好用的设计软件帮你提升设计水平办公室的一块砖
大学四年里因为基本没什么课，为了兴趣，在网上浏览了不少大牛的设计作品和经验分享，开始接触设计行业，掌握了一些设计软件，从而转行进入设计行业。今天就根据我的自学经验，和大家一起分享下这也适合新手尝试的设计软件吧！Pixso这是国内有名的软件公司万兴科技筹备了一年多推出的在线设计软件。我个人觉得是非常适合新手的，集原型，设计，交付，协作和资源管理于一体，UI设计功能方面可以说已经比较全面了，具备矢量网
Spark运行时架构 tooolik spark 架构大数据
目录一，Spark运行时架构二，YARN集群架构（一）YARN集群主要组件1、ResourceManager-资源管理器2、NodeManager-节点管理器3、Task-任务4、Container-容器5、ApplicationMaster-应用程序管理器6，总结（二）YARN集群中应用程序的执行流程三、SparkStandalone架构（一）client提交方式（二）cluster提交方式四、
信息安全国内外现状及技术要求示例（R155/R156） mini积木信息安全安全 mcu
国际政策、法规的现状与趋势鉴于对交通安全、社会安全甚至国家安全的重要影响，汽车网络安全、数据安全得到各相关国家和地区的高度重视，纷纷出台相关法规、标准。信息安全法规R155法规适用范围覆盖了乘用车及商用车，适用于M类、N类车型，装备了至少一个ECU的O类车型，以及具备L3及以上自动驾驶功能的L6和L7类车型。此法规适合于1958协议国（包括欧洲、日本、俄罗斯、澳大利亚等）。根据欧盟要求，从2022
探秘3D UNet-PyTorch：高效三维图像分割利器鲍凯印Fox
探秘3DUNet-PyTorch：高效三维图像分割利器在医学影像处理、计算机视觉和自动驾驶等领域，三维图像的理解与分析至关重要。而是一个基于PyTorch实现的深度学习模型，专为三维图像分割任务设计。本文将深入剖析该项目的技术细节，应用场景及特性，以期吸引更多的开发者和研究人员参与其中。项目简介3DUNet是2DUNet的三维扩展，其结构保持了卷积神经网络的对称性，采用跳跃连接的方式保留了不同尺度
Unity 热更之【YooAsset 热更】Unity 可以进行热更的资源管理系统，并【Android 端简单实现·案例热更】仙魁XAN Unity 进阶 unity YooAsset yoo Android 热更
Unity热更之【YooAsset热更】Unity可以进行热更的资源管理系统，并【Android端简单实现·案例热更】目录Unity热更之【YooAsset热更】Unity可以进行热更的资源管理系统，并【Android端简单实现·案例热更】一、简单介绍二、YooAsset引入工程三、Sample案例Android端热更四、Python服务器简单构建一、简单介绍Unity的资源管理系统不断发展，以适
Windows和Mac命令窗快速打开文件夹奔跑的呱呱牛 windows macos
Windowsexplorer.和macOSopen.命令详解1.Windowsexplorer.explorer是Windows上的文件资源管理器，用于通过命令行打开文件夹或文件。常用命令格式：explorer[选项][目标路径].表示当前目录，explorer.打开当前工作目录的文件资源管理器。常用参数：explorerC:\path\to\folder：打开指定的文件夹。explorerC:
基本数据类型和引用类型的初始值 3213213333332132 java基础
package com.array; /** * @Description 测试初始值 * @author FuJianyong * 2015-1-22上午10:31:53 */ public class ArrayTest { ArrayTest at; String str; byte bt; short s; int i; long
摘抄笔记--《编写高质量代码：改善Java程序的151个建议》白糖_ 高质量代码
记得3年前刚到公司，同桌同事见我无事可做就借我看《编写高质量代码：改善Java程序的151个建议》这本书，当时看了几页没上心就没研究了。到上个月在公司偶然看到，于是乎又找来看看，我的天，真是非常多的干货，对于我这种静不下心的人真是帮助莫大呀。看完整本书，也记了不少笔记
【备忘】Django 常用命令及最佳实践 dongwei_6688 django
注意：本文基于 Django 1.8.2 版本生成数据库迁移脚本（python 脚本） python manage.py makemigrations polls 说明：polls 是你的应用名字，运行该命令时需要根据你的应用名字进行调整查看该次迁移需要执行的 SQL 语句（只查看语句，并不应用到数据库上）： python manage.p
阶乘算法之一N! 末尾有多少个零周凡杨 java 算法阶乘面试效率
&n
spring注入servlet g21121 Spring注入
传统的配置方法是无法将bean或属性直接注入到servlet中的，配置代理servlet亦比较麻烦，这里其实有比较简单的方法，其实就是在servlet的init()方法中加入要注入的内容： ServletContext application = getServletContext(); WebApplicationContext wac = WebApplicationContextUtil
Jenkins 命令行操作说明文档 510888780 centos
假设Jenkins的URL为http://22.11.140.38:9080/jenkins/ 基本的格式为 java 基本的格式为 java -jar jenkins-cli.jar [-s JENKINS_URL] command [options][args] 下面具体介绍各个命令的作用及基本使用方法 1. &nb
UnicodeBlock检测中文用法布衣凌宇 UnicodeBlock
/** * 判断输入的是汉字 */ public static boolean isChinese(char c) { Character.UnicodeBlock ub = Character.UnicodeBlock.of(c);
java下实现调用oracle的存储过程和函数 aijuans java orale
1.创建表：STOCK_PRICES 2.插入测试数据： 3.建立一个返回游标： PKG_PUB_UTILS 4.创建和存储过程：P_GET_PRICE 5.创建函数： 6.JAVA调用存储过程返回结果集 JDBCoracle10G_INVO
Velocity Toolbox antlove 模板 tool box velocity
velocity.VelocityUtil package velocity; import org.apache.velocity.Template; import org.apache.velocity.app.Velocity; import org.apache.velocity.app.VelocityEngine; import org.apache.velocity.c
JAVA正则表达式匹配基础百合不是茶 java 正则表达式的匹配
正则表达式;提高程序的性能,简化代码,提高代码的可读性,简化对字符串的操作正则表达式的用途; 字符串的匹配字符串的分割字符串的查找字符串的替换正则表达式的验证语法 [a] //[]表示这个字符只出现一次 ,[a] 表示a只出现一
是否使用EL表达式的配置 bijian1013 jsp web.xml EL EasyTemplate
今天在开发过程中发现一个细节问题，由于前端采用EasyTemplate模板方法实现数据展示，但老是不能正常显示出来。后来发现竟是EL将我的EasyTemplate的${...}解释执行了，导致我的模板不能正常展示后台数据。网
精通Oracle10编程SQL(1-3)PLSQL基础 bijian1013 oracle 数据库 plsql
--只包含执行部分的PL/SQL块 --set serveroutput off begin dbms_output.put_line('Hello,everyone!'); end; select * from emp; --包含定义部分和执行部分的PL/SQL块 declare v_ename varchar2(5); begin select
【Nginx三】Nginx作为反向代理服务器 bit1129 nginx
Nginx一个常用的功能是作为代理服务器。代理服务器通常完成如下的功能：接受客户端请求将请求转发给被代理的服务器从被代理的服务器获得响应结果把响应结果返回给客户端实例本文把Nginx配置成一个简单的代理服务器对于静态的html和图片，直接从Nginx获取对于动态的页面，例如JSP或者Servlet，Nginx则将请求转发给Res
Plugin execution not covered by lifecycle configuration: org.apache.maven.plugin blackproof maven 报错
转：http://stackoverflow.com/questions/6352208/how-to-solve-plugin-execution-not-covered-by-lifecycle-configuration-for-sprin maven报错： Plugin execution not covered by lifecycle configuration:
发布docker程序到marathon ronin47 docker 发布应用
1 发布docker程序到marathon 1.1 搭建私有docker registry 1.1.1 安装docker regisry docker pull docker-registry docker run -t -p 5000:5000 docker-registry 下载docker镜像并发布到私有registry docker pull consol/tomcat-8.0
java-57-用两个栈实现队列&&用两个队列实现一个栈 bylijinnan java
import java.util.ArrayList; import java.util.List; import java.util.Stack; /* * Q 57 用两个栈实现队列 */ public class QueueImplementByTwoStacks { private Stack<Integer> stack1; pr
Nginx配置性能优化 cfyme nginx
转载地址：http://blog.csdn.net/xifeijian/article/details/20956605 大多数的Nginx安装指南告诉你如下基础知识——通过apt-get安装，修改这里或那里的几行配置，好了，你已经有了一个Web服务器了。而且，在大多数情况下，一个常规安装的nginx对你的网站来说已经能很好地工作了。然而，如果你真的想挤压出Nginx的性能，你必
[JAVA图形图像]JAVA体系需要稳扎稳打,逐步推进图像图形处理技术 comsci java
对图形图像进行精确处理，需要大量的数学工具，即使是从底层硬件模拟层开始设计，也离不开大量的数学工具包，因为我认为，JAVA语言体系在图形图像处理模块上面的研发工作，需要从开发一些基础的，类似实时数学函数构造器和解析器的软件包入手，而不是急于利用第三方代码工具来实现一个不严格的图形图像处理软件...... &nb
MonkeyRunner的使用 dai_lm android MonkeyRunner
要使用MonkeyRunner，就要学习使用Python，哎先抄一段官方doc里的代码作用是启动一个程序（应该是启动程序默认的Activity），然后按MENU键，并截屏 # Imports the monkeyrunner modules used by this program from com.android.monkeyrunner import MonkeyRun
Hadoop-- 海量文件的分布式计算处理方案 datamachine mapreduce hadoop 分布式计算
csdn的一个关于hadoop的分布式处理方案，存档。原帖：http://blog.csdn.net/calvinxiu/article/details/1506112。 Hadoop 是Google MapReduce的一个Java实现。MapReduce是一种简化的分布式编程模式，让程序自动分布到一个由普通机器组成的超大集群上并发执行。就如同ja
以資料庫驗證登入 dcj3sjt126com yii
以資料庫驗證登入由於 Yii 內定的原始框架程式, 採用綁定在UserIdentity.php 的 demo 與 admin 帳號密碼: public function authenticate() { $users=array( &nbs
github做webhooks：[2]php版本自动触发更新 dcj3sjt126com github git webhooks
上次已经说过了如何在github控制面板做查看url的返回信息了。这次就到了直接贴钩子代码的时候了。工具/原料 git github 方法/步骤在github的setting里面的webhooks里把我们的url地址填进去。钩子更新的代码如下： error_reportin
Eos开发常用表达式蕃薯耀 Eos开发 Eos入门 Eos开发常用表达式
Eos开发常用表达式 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2014年8月18日 15:03:35 星期一 &
SpringSecurity3.X--SpEL 表达式 hanqunfeng SpringSecurity
使用 Spring 表达式语言配置访问控制，要实现这一功能的直接方式是在<http>配置元素上添加 use-expressions 属性： <http auto-config="true" use-expressions="true"> 这样就会在投票器中自动增加一个投票器：org.springframework
Redis vs Memcache IXHONG redis
1. Redis中，并不是所有的数据都一直存储在内存中的，这是和Memcached相比一个最大的区别。 2. Redis不仅仅支持简单的k/v类型的数据，同时还提供list，set，hash等数据结构的存储。 3. Redis支持数据的备份，即master-slave模式的数据备份。 4. Redis支持数据的持久化，可以将内存中的数据保持在磁盘中，重启的时候可以再次加载进行使用。 Red
Python - 装饰器使用过程中的误区解读 kvhur JavaScript jquery html5 css
大家都知道装饰器是一个很著名的设计模式，经常被用于AOP(面向切面编程)的场景，较为经典的有插入日志，性能测试，事务处理，Web权限校验， Cache等。原文链接：http://www.gbtags.com/gb/share/5563.htm Python语言本身提供了装饰器语法（@），典型的装饰器实现如下： @function_wrapper de
架构师之mybatis-----update 带case when 针对多种情况更新 nannan408 case when
1.前言. 如题. 2. 代码. <update id="batchUpdate" parameterType="java.util.List"> <foreach collection="list" item="list" index=&
Algorithm算法视频教程栏目记者 Algorithm 算法
课程：Algorithm算法视频教程百度网盘下载地址： http://pan.baidu.com/s/1qWFjjQW 密码: 2mji 程序写的好不好,还得看算法屌不屌！Algorithm算法博大精深。一、课程内容：课时1、算法的基本概念 + Sequential search 课时2、Binary search 课时3、Hash table 课时4、Algor
C语言算法之冒泡排序 qiufeihu c 算法
任意输入10个数字由小到大进行排序。代码： #include <stdio.h> int main() { int i,j,t,a[11]; /*定义变量及数组为基本类型*/ for(i = 1;i < 11;i++){ scanf("%d",&a[i]); /*从键盘中输入10个数*/ } for
JSP异常处理 wyzuomumu Web jsp
1.在可能发生异常的网页中通过指令将HTTP请求转发给另一个专门处理异常的网页中: <%@ page errorPage="errors.jsp"%> 2.在处理异常的网页中做如下声明： errors.jsp: <%@ page isErrorPage="true"%>，这样设置完后就可以在网页中直接访问exc

[文献提炼] 车联网中资源分配的问题建模 又三篇

前言

Model-Free Ultra Reliable Low Latency Communication (URLLC): a Deep Reinforcement Learning Framework

Learn to Compress CSI and Allocate Resources in Vehicular Networks

Intelligent Resource Management Based on Reinforcement Learning for Ultra-Reliable and Low-Latency IoV Communication Networks

总结

你可能感兴趣的:(V2X,资源管理,自动驾驶)

[文献提炼] 车联网中资源分配的问题建模又三篇