【深度强化学习】强化学习的基本概念
文章目录
- 前言
- 第一章:强化学习的基本概念
-
- 学习——监督, 无监督与强化学习
- 强化学习的体系与联系
-
- Reward 奖励
- Agent
- Environment
- Actions
- Observation
- 马尔科夫决策过程
-
- 马尔科夫链
- 马尔科夫奖励过程
- 马尔科夫决策过程
- Policy
- 总结
前言
重读《Deep Reinforcemnet Learning Hands-on》, 常读常新, 极其深入浅出的一本深度强化学习教程。 本文的唯一贡献是对其进行了翻译和提炼, 加一点自己的理解组织成一篇中文笔记。
原英文书下载地址: 传送门
原代码地址: 传送门
第一章:强化学习的基本概念
强化学习是一种将时间维度 融入 学习方程, 更接近于人类认知的人工智能。 本章主要从以下三点展开:
- 强化学习 (Reinforcement Learning, RL) 与 其他 机器学习 (Machine Learning, ML) 的区别: 监督 (supervised) 与 无监督 (unsupervised) 学习
- 强化学习的具体主要体系
- 强化学习的理论基础: 马尔科夫决策过程 (Markov decision processes)
学习——监督, 无监督与强化学习
- 文本分类: 这条邮件是否是垃圾信息?
- 图像识别和目标定位:这张图片是否含有 猫,狗,或者其他物品?
- 回归问题:能否通过天气传感器给出的一些信息, 推断明天的天气?
- 情感分析:客户的这份评论, 满意度是多少?
以上是经典的 监督学习的例子, 他们有共同的特点:我们从 已知答案的大量样本 进行学习, 来获得能对 类似分布的 尚未出现过的 样本 输出期望结果的模型。如例2, 给予模型100万张图片进行学习, 可以人为地告知其 标签 (labe), 即图中是猫或狗。 经过足够的监督学习后, 对于一张从未出现过的图片, 模型已能准确判断其 是否为猫或狗。
另一个对应的概念就是 无监督学习。其认为 **可供学习的样本并无对应的已知标签。**同如例2, 有100张图片, 但无人告知,没张图片中是猫或是狗(标签)。 其主要目的是为 学习 数据集的 一些 隐藏结构。 一个常见的例子就是 聚类 (clustering of data): 将样本数据们 组合成 不同的集群(clusters),揭示数据之间的联系。
上图中, 数据点没有任何的标签, 但通过聚类算法可以根据数据点本身的数据,对其进行聚类,如上图, 数据点明显地被分为了两大类。 聚类的具体不再展开, 这里给出两个参考:
维基百科:聚类
对几种聚类算法的简单中文介绍
另一个 无监督的学习的经典例子, 就是 生成对抗网络(Generative Adversarial Networks, GAN ), 简单介绍: 该模型包括两部分:
- 生成网络: 负责产生 伪造的 数据, 尽可能使对抗网络无法鉴别。
- 对抗网络:负责鉴别 伪造的 数据, 尽可能识别出生成网络生成的数据。
比如, 现在手头有100万张, 猫,狗的 图片, 生成网络, 负责输出 伪造的 图片, 对抗网络,则负责鉴别两者的差别。 两者交替训练, 对抗网络的识别能力越来越强, 为了迷惑之, 生成网络生成的图片也越来越逼真。 这里也给出GAN的简单参考:
知乎:GAN的简单原理
强化学习则是第三种情况: 介于监督与非监督之间。 其使用了许多监督学习的经典方法: 神经网络, 随机梯度下降法(SGD), 和 后向传播等。 另一方面, 他又没有 已定义好的 标签。
接下来是对 强化学习概念 简单释义的一个例子:

一只机器(robot)小老鼠, 在一个迷宫之中。 一些点上, 有着食物, 一些点上则有着电击。 这个小老鼠可以上下左右移动。 每一时刻, 假设它可以观察到 迷宫的整体情况 (state), 来对下一步的**动作 (action) **做出决定。 目标是尽可能地拿到更多的食物,避免受到电击, 这代表了奖励(reward)(比如食物代表reward + 1, 而电击代表 reward - 1)。显然,小老鼠最终的目标是为了奖励最大化。 比如: 小老鼠可以选择经受1次电击,而获得大量的食物, 这显然比 呆在原地不动更好 (即前者的reward大于后者)。
一种做法是:把所有可能的迷宫情况和对应的最佳动作都 写入 机器小老鼠的程序中。 但这样显然不合理: 开销巨大, 且如果迷宫稍加变化, 便无法应对了。 我们希望的是这样的方法:让机器小老鼠自己学会, 去避开电击, 获取更多的食物。
强化学习就是这样一种工具。 他不像监督学习, 依赖于已经定制好的标签: 没有任何标签告知了小老鼠当前的状态是好抑或是坏, 抑或是应该采取怎样的动作。
然而, 我们也并非如 无监督学习那样 一无所知 (blind)。 ——强化学习有一个奖励系统 (reward system)。我们可以通过观测(observation), 每个动作执行后, 奖励的变化(上升或是下降), 从而学习如何去执行更好的动作。 比如电击后发现奖励下降, 那就会慢慢地学到, 应该尽可能做出,避开电击的动作决策。
然而, 相比于监督和非监督学习, 强化学习显得更具挑战性:
- 强化学习的观测决定于其行为 (behavior)本身。 如果模型本身(可以理解为agent, 即做出决策者)一直选择无意义的动作, 那得到的观测也毫无意义: 既不能告诉你避开不好的动作, 也无法告知你何为好的动作。以小鼠迷宫为例, 如果小鼠的决策是一直原地打转, 那你显然也无从得知, 应当尽可能的获取更多食物, 避开电击——因为你压根不会有相关观测的经验。如果agent一直做出错误的决策, 那永远也无法获得更大的reward, 即,观测到的一直是 很差 的情况。 这些观测的经验, 在机器学习的领域中, 可以被认为是非 独立不相关 (non i.i.d.)的数据(都是垃圾数据), 不利于训练。
- 另一个问题在于, agent 不能仅仅利用(exploit) 已学到的策略(policy), 还要进一步在环境中学习 (explore)。谁知道呢? 也许采用之前一个从未使用过的动作, 就可以使reward大幅提升。 但同样的, 过多的开发尝试, 可能也会使得reward下降(agent也会遗忘之前的策略)。因此要在探索 (exploration) 和 利用 (exploitation) 中,获取一种平衡。 就像实际生活中: 我应该去这家吃过的餐厅还是再去尝试那家新的餐厅呢?永远没有标准的回答。
- 第三个难点在于, 奖励很多时候严重滞后于动作。 比如在象棋游戏中, 每一步单独看起来没什么的下法可能改变了整个局势。
尽管有这些挑战, 强化学习 再近年还是取得了重大突破和成功,在研究领域和实际中变得愈发活跃。
强化学习的体系与联系
强化学习的两个主体: Agent 和 Environment。 如上例中的 老鼠 与 迷宫。
之间的交互: 动作 Actions, 奖励 Reward, 和 观测 Observations。

Reward 奖励
这是要讨论的第一个概念。 奖励 可以是正数,也可以是复数; 可以很大, 可以很小。 但是, 他只是一个数, 一个标量 (scalar), 用以评价我们的行为 (behavior) 。 奖励获取的频率也没有限制。 一般而言, 都是在 每个 时间戳 (timestamp) 或者 每个环境交互点 (interaction)获取。
需要注意的是, 奖励 是 局部的 (local), 即他只反映了当前动作的成功与否。 当前得到了一个巨大的奖励, 并不意味着一秒后不会面临窘境: 就像抢劫银行, 在抢劫成功的时候,看上去这是一个奖励巨大的决定, 直到你意识到即将被捕。
因此,Agent所要做出的决策, 是使得一系列动作的累加奖励 最大化。
Agent
Agent就是通过执行动作, 获取观测, 得到奖励 来与 环境 进行交互 的 决策者。 (上例中的小老鼠)。
Environment
环境就是 除Agent 以外的 外界事物。 最一般的情况, 整个宇宙(除去Agent), 当然这显然过头了, 超出了计算机的承受范围, 更合理的定义是:
环境就是Agent外部, 与Agent 进行交互的, 为Agent 提供 Reward, 接受Agent的Action并发生改变, 返还包括Reward 在内的 Observation 信息。
Actions
动作 是 Agent 可以 在 环境中 执行的 操作。 动作 可以 是 游戏中的移动规则。
动作可以分为 连续, 和 离散。 离散动作是取自一个有限的集合: 如 向左, 向右。
连续动作比如: 具体开往哪个方向(31°方向), 具体多少速度(11.5km/h)。
Observation
观测 是 除了 Reward之外的第二个 环境 给予 Agent 信息的渠道。 我认为, 这就是 当前环境与决策相关的状态:比如老鼠-迷宫例子中, Observation指的就是每走一步, 迷宫的整体布局信息: 如食物具体在哪, 电击在哪等信息。 而Agent(老鼠)依赖于这些信息做决策。 他与State的区别在于: State的范围更广一些, 而Observation更相关。 比如 State 可能还包括, 迷宫外面的道路,等等。 而 Observation则专注于小鼠迷宫这个小任务。
下面有对几个概念的更详细举例:
| 例子 | 奖励 | 动作 | 观测 | 广义State |
|---|---|---|---|---|
| 金融交易 | 交易的总收益 | 买进/卖出/不操作 | 股票价格/相关新闻 | 你今天呆在家与否的决定 |
| 象棋 | 胜负 | 每一步棋的下法 | 棋局现状 | 对方棋手的情绪,风格 |
| 电脑游戏 | 游戏内得分 | 游戏内的操作 | 游戏当前信息(地图,位置等) | 联机玩家的网络状态 |
| 训练小狗 | 喂它或打它 | 小狗接飞盘/不接 | 飞盘的位置 | 你女朋友的心情 |
马尔科夫决策过程
马尔科夫链被广泛地用于计算机科学的各个领域, 这是 强化学习的 理论基础, 却不仅局限于 强化学习。
马尔科夫链
Markov Process (MP), 也被称为Markov Chain, 即 马尔科夫链。
现在假设, 有一个你面前的, 只能观察 的 系统 , 你的观察被称为 States。这个系统 所有可能的状态 (possible states) 被称为 状态空间 (State Space)。我们要求这个空间是 有限的 。你的观测组成了一个 状态序列 (state sequence), 或者 一个 链 (chain) (这也是为什么 Markov Process 被称为 Markov Chain)。举例, 我们可以观测 城市每天的 天气, 那么 一个链 可以类似这样: [sunny, sunny, sunny, rain,…], 这样, 也被称为 历史 (history)。
如果被称为 马尔科夫链, 必须满足 马尔科夫性质 (Markov Property), 即:
系统的未来状态只与当前状态State有关, 而与历史无关。
以刚刚的天气 系统为例, 马尔科夫性质表明:** 如果当天是晴天, 那么第二天天下雨的概率是一样, 与当天前的晴雨关系无关, 即只和当天的状态相关**。 显然, 这在实际中不太合理, 但这个例子主要是为了让我们理解马尔科夫性质。 显然, 我们可以让我们的系统更复杂一些: 通过拓展状态空间。比如, 我们可以增加季节因素, 那么我们的观测可以描述为: [sunny+summer, sunny+winter, rainy+summer, rainy+winter]。
如果系统满足了马尔科夫性质, 那么 转移概率 (transition probabilities) 就可以用 **转移矩阵 (transition matrix)**来加以描述。 这是一个 KaTeX parse error: Undefined control sequence: \timesN at position 2: N\̲t̲i̲m̲e̲s̲N̲的矩阵, N N N就是状态空间的大小。 第 i i i行第 j j j列的元素即代表 由状态 i i i转换成 j j j的概率。
比如, 一个简单的例子:
| 晴天 | 雨天 | |
|---|---|---|
| 晴天 | 0.8 | 0.2 |
| 雨天 | 0.1 | 0.9 |
因此, 对马尔科夫链的正式定义应该为:
- 系统可能的状态集合 (状态空间)
- 转移矩阵
可以注意到马尔科夫链最重要的性质: 稳定。 转移矩阵是不变的。 这也印证了马尔科夫性质: 后续状态只与当前状态有关。 显然, 如果转移矩阵是变化的, 那就说明我们的系统受到除了当前状态以外的因素的影响。
马尔科夫奖励过程
在上一节中, 转移矩阵刻画了 从 State i i i 转移到 State j j j 的 概率。 但在实际中, 每一次转变应该有其对应的奖励reward——比如小鼠向上移动一格,吃到了食物。 因此, 也应当有一个 和转移矩阵类似的奖励矩阵。当然,需要提到的是, 很多时候奖励只和执行Action后的当前状态有关, 而与前一状态无关——比如小鼠,无论是上移一格吃到食物还是下移一格吃到,奖励是一样的。 基于这样的性质, 奖励矩阵可以大幅简化。 但这样的情况不是必然的。
与此同时, 有另一个概念 : return。 对于一个马尔科夫过程, 我们定义 t t t时刻的return为:
G t = R t + 1 + γ R t + 2 + … = ∑ k = 0 ∞ γ k R t + k + 1 G_{t}=R_{t+1}+\gamma R_{t+2}+\ldots=\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1} Gt=Rt+1+γRt+2+…=k=0∑∞γkRt+k+1
这里 R t R_t Rt即代表 t t t时刻的reward。 而 γ \gamma γ则代表折扣因子(discount factor)。 从公式可以看出, return不仅仅包括了当前状态的奖励, 还包括了后续状态的奖励。 这也是非常合理的, 毕竟我们做决策的时候,应当有长远眼光——即不能只着眼于眼前的奖励。 而折扣因子,则代表了这样的物理意义: 当 γ = 0 \gamma=0 γ=0时, return就等于当前的reward, 即短视的策略, 只注重当前利益。 当 γ = 1 \gamma=1 γ=1的时候, return 就等于后续所有reward之和, 就代表长远目光。
然而, 仅从上式可以发现, return的定义并不合理。 对于不同的马尔科夫链, 同一个State所对应的return会截然不同。 因为return的具体值涉及后续的具体状态。 因此,一种方式是计算return的数学期望, 这也被定义为 当前状态的价值(the value of State)
V ( s ) = E [ G ∣ S t = s ] V(s)=\mathbb{E}\left[G | S_{t}=s\right] V(s)=E[G∣St=s]
书中举了一个简单的例子:
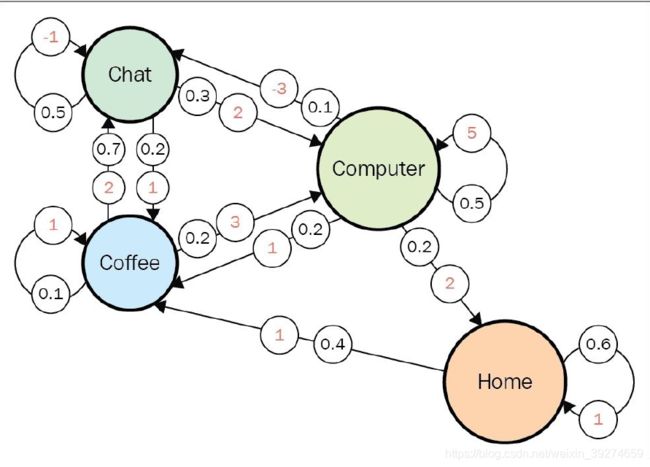
上图中, 共有4个状态State:Chat, Computer, Coffer, Home, 他们之间的连线, 红色数字代表这一转移的reward, 黑色数字代表转移的概率。 我们先假设折扣因子为0。显然,由Value的计算公式 有:
V ( chat ) = − 1 ∗ 0.5 + 2 ∗ 0.3 + 1 ∗ 0.2 = 0.3 V ( coffee ) = 2 ∗ 0.7 + 1 ∗ 0.1 + 3 ∗ 0.2 = 2.1 V(home) = 1 ∗ 0.6 + 1 ∗ 0.4 = 1.0 V(computer) = 5 ∗ 0.5 + ( − 3 ) ∗ 0.1 + 1 ∗ 0.2 + 2 ∗ 0.2 = 2.8 \begin{array}{l} V(\text { chat })=-1 * 0.5+2 * 0.3+1 * 0.2=0.3 \\ V(\text { coffee })=2 * 0.7+1 * 0.1+3 * 0.2=2.1 \\ \text { V(home) }=1 * 0.6+1 * 0.4=1.0 \\ \text { V(computer) }=5 * 0.5+(-3) * 0.1+1 * 0.2+2 * 0.2=2.8 \end{array} V( chat )=−1∗0.5+2∗0.3+1∗0.2=0.3V( coffee )=2∗0.7+1∗0.1+3∗0.2=2.1 V(home) =1∗0.6+1∗0.4=1.0 V(computer) =5∗0.5+(−3)∗0.1+1∗0.2+2∗0.2=2.8
由此,Computer是最有价值的状态。
但是,如果 γ \gamma γ取1呢? 这个问题就无解了,因为每个状态的Value都会算成无穷——因为没有一个状态是结束状态, 所以value会无限计算下去, 没有终点。 因此, 一般而言, 在实际中, 会取折扣因子 为 γ = 0.9 \gamma=0.9 γ=0.9 或 0.99 0.99 0.99, 既包含了远见考虑, 又不至于无限计算。 但这样Value的值仍是几百项的累加和, 不过这恰恰是计算机所擅长的工作, 目前我们只需要有这样一个概念。
马尔科夫决策过程
Markov Decision Process。首先, 我们有一个有限的 Action 动作空间。 即 Agent 的 Action Space。 与此同时:我们将之前的转移图形(二维方形) 拓展 为 立方体(Cube)。

如图, 这是一个三维的情况: 源状态 (Source State)由高度刻画, 目标状态(Target State)由宽度刻画, 动作则由深度(depth)刻画。 比如图中的这个红点,代表的则是: 当采用 动作 k k k时, 状态 i i i 转移到 状态 j j j的概率。
举一个例子, 一个机器人 处于 一个 3 × 3 3 \times 3 3×3 的 方格中, 机器人可以上下左右移动。 同时, 机器人的朝向也有四种情况 (也是前后左右)。 因此,机器人共有 3 × 3 × 4 3\times 3\times 4 3×3×4 即36种状态。 同时, 假设机器人并不是那么灵敏。 比如,存在10%的可能性, 当执行了 前进动作时, 机器人转向了, 但并未改变位置。 同理, 也可能改变了位置,而未转向。 因此这时二维的转移矩阵已经不够描述马尔科夫链, 而需要类似上图的三维方体来进行描述。
同理, 可以将reward加上。 这时, reward不仅与原状态及目标状态有关, 也与动作有关——即过程也是重要的。 比如你认真学习了, 啥都没学到, 与啥都没干, 虽然原状态和目标状态一致, 但reward理应不同——认真学习的过程你可能掌握了学习的经验,等等。
Policy
完善了马尔科夫链的体系后, 还需介绍的核心概念是: 策略 (policy)。
策略的简单定义就是:一种规则, 控制Agent的行为。 以刚刚的机器人例子为例, agent可以采取以下多种不同的策略:
- 乱移, 无视任何事物
- 通过检查过去经验, 尝试避开障碍物
- 滑稽的旋转来取悦其创造者
- 随机移动, 如同喝醉一样。。
这些都是策略。 同时, 我们也记得:强化学习的目的是最大化return(可以视作reward的加权累加)。而好的策略就是如此。 正式地,我们把策略定义为:
π ( a ∣ s ) = P [ A t = a ∣ S t = s ] \pi(a | s)=P\left[A_{t}=a | S_{t}=s\right] π(a∣s)=P[At=a∣St=s]
注意,这里定义的策略代表: 当状态为 s s s时, 采取动作 a a a的概率。这一点在策略中加入了随机性——也许不被看好的动作也有被尝试的可能性(概率不等于0)。 这一点非常重要。 如果对于某个动作, 概率为1, 而其他动作为0 ,这样的策略也被称为确定性策略(deterministic policy)。
如果我们的策略固定不变, 那么 MDP (Markov Decision Process)则可以退化为 MRP (Markov Reward Process) 。因为状态定了的时候, 选取的动作概率也已确定, Action的维度可以省略。
总结
这一章介绍了极具挑战性,但基础且重要的知识。 下一章开始, 会介绍RL的相应实战。
