完全理解ST稀疏表在线处理RMQ问题及RGQ问题

ST是什么

ST S T 的全称是 SparseTable S p a r s e T a b l e 。谷歌上的解释如下：

Sparse Table is a data structure that answers static Range Minimum Query (RMQ). It is recognized for its relatively fast query and short implementation compared to other data structures.

稀疏表概念用于对一组静态数据进行快速查询（元素不会更改）。它进行预处理，以便有效地回答查询。

ST S T 的优势就是可以在 O(1) O ( 1 ) 的时间复杂度内查询任意区间的结果，而只需要花费 O(nlogn) O ( n l o g n ) 的预处理时间。因此基于 ST S T 稀疏表的算法就是在线算法。

RMQ问题和RGQ问题

这两个问题的全称分别如下：

• RMQ：Range Minimum Query
  区间最大最小值问题

• RGQ： Range GCD Query
  区间最大公约数问题

这两个问题用常规方法解，单次询问的时间复杂度为 O(n) O ( n ) ，在大量的询问情景中，这种时间复杂度是不能接受的。

当然，这两个问题可以用线段树维护处理，单次询问的时间复杂度为 O(logn) O ( l o g n ) ， O(logn) O ( l o g n ) 在 n n 很大的时候会导致常数很大，有时候也不行。

如果有单次询问的时间复杂度为 O(1) O ( 1 ) 的算法就好了，有，就是ST稀疏表维护RMQ问题和RGD问题，简称 ST S T 算法。

什么样的问题适合ST算法

正如标题所说，RMQ问题和RGQ问题适合 ST S T 算法，那么这两个问题有什么特性呢，以RMQ问题举例。

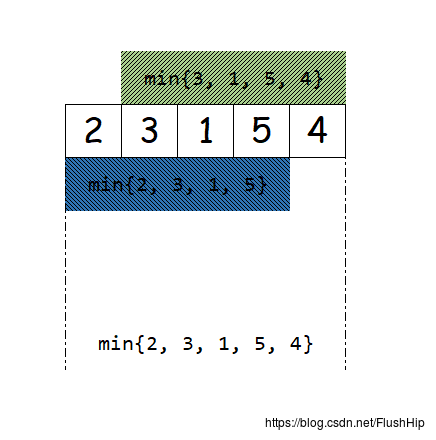
求{2, 3, 1, 5, 4}的最小值，可以通过求出a = min{2, 3, 1, 5}, b = min{3, 1, 5, 4}, ans = min{a, b}求出。

可以看到，求一个大区间的最小值，可以通过求两个小区间的最小值来求得，前提是这两个小区间的并集是这个大区间，至于有没有交集，对结果没有影响。所以求{2, 3, 1, 5, 4}的和，就不能这么做了。

因此，总结一下，如果一个大区间问题可以由两个小区间(这两个小区间的并集是这个大区间)得到，这两个小区间是否有重叠对大区间的结果没有任何影响。那么这类问题就可以用 ST S T 算法来做。这和分治算法有点像，但是核心要求完全不一样，分治算法的子问题不能有重叠。而 ST S T 算法对这一项没有要求。

显然，RMQ问题和RGQ问题都是上述结论的情形。

ST算法原理

ST S T 算法是在线算法，在线算法都要预处理，因此，原理分两部分，预处理和查询。

上面加粗的文字其实就是 ST S T 算法的核心思想，它讲了两个点：

• 要把大区间分成小区间(预处理)
• 利用重叠小区间得出大区间的结果(查询)

预处理

预处理是核心，正如上面所说的，要把大区间分成小区间，那么这些小区间的长度为多少呢？答案是2的幂次。

为什么呢，因为 2i=2∗2i−1 2 i = 2 ∗ 2 i − 1 ，求出一个2的幂次，可以用这个结果继续推出下一个2的幂次，而且如果用2的幂次做区间长度，对于一个长度为 n n 的区间，最多只会有 logn l o g n 种不同长度的小区间，它们的区间长度依次是 20,21,⋯,2logn 2 0 , 2 1 , ⋯ , 2 l o g n 。

因此，预处理的任务是求出所有上述区间长度的区间结果，如下图：

可以看到，长度为1的区间有5个，长度为2的区间有4个，长度为4的区间有2个。我们的任务求出这 5+4+2=11 5 + 4 + 2 = 11 个区间的结果，那么如果长度为 n n 的区间，要求出多少个这样的子区间呢，从图上可以看出，会有 logn l o g n 层不同长度的子区间，每层的个数取最大值 n n ，那么就有 nlogn n l o g n 个子区间是要通过预处理求出来的。

同时，看下图中的箭头，下一层的子区间结果可以借用上一层的结果得出，即 2i=2i−1+2i−1 2 i = 2 i − 1 + 2 i − 1 。

其实观察这个预处理的本质，就是区间DP，ST算法就是用区间DP来预处理的，动态规划的思想，只不过这个区间DP是建立在二进制(待会要用到，这里先提出来)上的，即 100=10+10 100 = 10 + 10 , 1000=100+100 1000 = 100 + 100 等等。

查询

查询这个地方比较有味了，就是利用重叠小区间得出大区间的结果，那么给出一个大区间如何找到符合规则的两个小区间呢？而且小区间的长度只有2的幂次。比如，对于序列{2, 3, 1, 5, 4}，你找{2, 3}和{3, 1}这两个小区间是肯定不行的，这两个小区间没有覆盖大区间。

这里说一种方法，先决定长度，两个区间的长度加起来一定要大于原来区间的长度，为了方便期间，这两个区间的长度一样。如下图：

我们要找一个区间，这个区间不能覆盖大区间，但是这个区间的两倍要覆盖大区间(超过大区间没关系，我们可以平移)。

我们发现上图的区间长度长度为4的区间满足这个条件。但是两倍后整个区间就超过了原区间，这样会把不属于原区间的结果也包含进来。解决的办法就是平移后一个区间，使其右端点和原区间的右端点对齐，如下图：

中间会有重叠的，不过这之前就说了，重叠对结果不会有影响。

ST算法步骤流程

上面都在讲 ST S T 算法的核心原理，那么究竟如何在代码的层面上实现这个算法呢？这里面还是有点东西的。

预处理

预处理的方法前面说了，区间DP的思想求出所有子区间的结果，之前在原理中已经说得很清楚了，这里不细说。

讲下代码如何写。

定义dp[left][i]：左端点为left，且区间长度为2的i次幂的区间结果。

那么这个状态转移方程就是：dp[left][i] = func(dp[left][i - 1], dp[left + (1 << (i - 1))][i - 1])。

void pretreat(BF func)
{
    for (int left = 0; left < n; dp[left][0] = arr[left], ++left) {}
    for (int i = 1; i < Log2[n]; ++i)
        for (int left = 0; left + (1 << i) <= n; ++left)
            dp[left][i] = func(dp[left][i - 1], dp[left + (1 << (i - 1))][i - 1]);
}

没看明白的可以看看上面的原理，func是一个二元函数binary_function。可以是max、min、gcd。

int min(int a, int b)
{
    return a < b ? a : b;
}

int max(int a, int b)
{
    return a > b ? a : b;
}

int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a % b);
}

查询

查询的原理上面已经说得很清楚了，现在的问题是如何找到那个不大也不小的小区间使得这个区间不能覆盖大区间，但是这个区间的两倍要覆盖大区间。我们把这个区间的长度写成二进制，比如 len=7(1011)2 l e n = 7 ( 1011 ) 2 ，我们每次去二进制中最高一位的1就可以满足这个要求了， (1000)2<(1011)2 ( 1000 ) 2 < ( 1011 ) 2 且两倍 1000 1000 等于 (1000)2<<1=(10000)>(1011)2 ( 1000 ) 2 << 1 = ( 10000 ) > ( 1011 ) 2 。

获取最高一位1的位置可以用下面代码：

log(len) / log(2);

不过更推荐的是把1 ~ len最高一位1的位置都递推预处理出来，这样比较快。

void init()
{
    for (int i = 1; i < MAX_SIZE; ++i)
        Log2[i] = Log2[i >> 1] + 1;
}

查询区间[l, r)结果的代码如下：

// [l, r)
int query(int l, int r, BF func)
{
    return func(dp[l][Log2[r - l] - 1], dp[r - (1 << Log2[r - l] - 1)][Log2[r - l] - 1]);
}

原理请对照上图。

完整测试代码

#include 

using namespace std;

#define MAX_SIZE (1 << 10)
#define TOP (int)(log(MAX_SIZE) / log(2)) + 1

int arr[MAX_SIZE];
int dp[MAX_SIZE][TOP];
int Log2[MAX_SIZE];
int n;

int min(int a, int b)
{
    return a < b ? a : b;
}

int max(int a, int b)
{
    return a > b ? a : b;
}

int gcd(int a, int b)
{
    return b == 0 ? a : gcd(b, a % b);
}

// BF : binary_function
typedef int (*BF) (int, int);

void init()
{
    for (int i = 1; i < MAX_SIZE; ++i)
        Log2[i] = Log2[i >> 1] + 1;
}

void pretreat(BF func)
{
    for (int left = 0; left < n; dp[left][0] = arr[left], ++left) {}
    for (int i = 1; i < Log2[n]; ++i)
        for (int left = 0; left + (1 << i) <= n; ++left)
            dp[left][i] = func(dp[left][i - 1], dp[left + (1 << (i - 1))][i - 1]);
}

// [l, r)
int query(int l, int r, BF func)
{
    return func(dp[l][Log2[r - l] - 1], dp[r - (1 << Log2[r - l] - 1)][Log2[r - l] - 1]);
}

int main()
{
    init();
    for (; EOF != scanf("%d", &n); ) {
        for (int i = 0; i < n; scanf("%d", &arr[i++])) {}
        // arr[0] = 2; arr[1] = 1; arr[2] = 4; arr[3] = 3; arr[4] = 5;
        BF pFunc = min;
        pretreat(pFunc);
        for (int l, r; ; ) {
            scanf("%d%d", &l, &r);
            assert(l < r);
            assert(0 <= l && l <= n);
            assert(0 <= r && r <= n);
            printf("[%d, %d) : %d\n", l, r, query(l, r, pFunc));
        }
    }
    return 0;
}

时间空间复杂度

通过代码可以发现:
预处理的时间复杂度是 O(nlogn) O ( n l o g n ) ，查询的时间复杂度是 O(1) O ( 1 ) ；
预处理的空间复杂度是 O(nlogn) O ( n l o g n ) ，查询的空间复杂度是 O(1) O ( 1 ) ；

ST算法在线解决RMQ和RGQ举例和应用

详情见博客ST算法处理RMQ和RGQ问题的4个例题。

总结

ST S T 算法的原理应该是说得很仔细很清楚了，实现的过程不重要，重要的是理解原理，理解那种二进制的思想。

正如之前一直所说的一样， ST S T 算法只是一个脚手架。它能帮我们高效处理实际问题的一部分，其余的部分就要考我们自己去思考和解决了。

---

参考：

• 树上倍增法求最近公共祖先LCA的二进制思想
• https://www.geeksforgeeks.org/sparse-table/
• https://www.hackerearth.com/zh/practice/notes/sparse-table/