二分图最佳完美匹配——KM算法
前情概要
学km算法之前,笔者还是希望大家已经掌握了匈牙利算法——也就是对于求解二分图最大匹配的算法。学习本算法的前提除了已经掌握C++语言之外,还需要掌握邻接表存图法,不会的朋友这里有传送门 [微笑]
邻接表存图法
km算法是匈牙利算法的改进,然而他只能是在被深搜的点本来就可以匹配的情况下才能使用(为什么后面告诉你),他可以让匹配后所有匹配边权重加起来最大或者最小——计算机算法总是寻找这些“最”。如果大家对什么是二分图或者什么是二分图最大匹配仍存在疑问,可以参考这篇blog,向你保证你会得到你想要的答案:二分图最大匹配——匈牙利算法
KM算法vs匈牙利算法
我当你已经会了前情概要里面提到的所有东西了哦~
以下内容仅仅是概要,样例模拟才是真正的详解哦
KM算法在什么地方和匈牙利不同才让它具备匹配后所有匹配边权重加起来最大或者最小的神奇特性呢?其实匈牙利算法使用了一个特殊的工具——点标。
每一个左边点都有属于自己的点标,这个点标有一个值,这个值等于这个点的所有出边中最大权值出边的权值。
每一个右边点都有属于自己的点标,我们统一设置为0。
然后我们规定:只有左右两边的点可连通而且这两个点的点标之和等于他们连通的边的权值,才可以匹配。
我先上一个图:

点2就有3个出边,其中最大的出边权值是3,所以点2的点标等于3。显然点7的点标是0,3+0等于他们连通的边的权值,所以我们认为这两个点是可以匹配的。初始化点标之后就是酱紫:
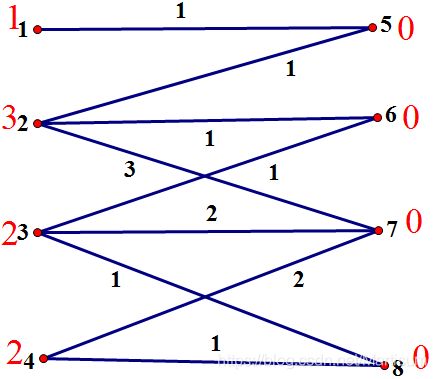
我们需要告知哪一些点是在左边的,并且设立一个数组 l 来存储左边的点,lx 来表示左边的点的总点数。
我们如图匈牙利算法一样,都会从每一个点出发挨个儿深搜,然而这一次我们的深搜多了一个条件,就是只有左右两边的点可连通而且这两个点的点标之和等于他们连通的边的权值,才可以匹配。所以当因为这个条件不匹配的时候,我们就把当前深搜路径上所有左边点的权值减少d,右边增加d,维持平衡。这样做,可以使当前左边的点有更多的选择,然后我们重新深搜。
而为了使我们匹配的边尽量大,所以d要尽量小。这样就可以使左边点的点标尽量大,就可以挑选边权比较大的边。我们暂且把每一次深搜因为**只有左右两边的点可连通而且这两个点的点标之和等于他们连通的边的权值,才可以匹配。**这个原因而无法匹配时把产生的d给计算出来,存到一个叫做slack的数组里面。那么如何让slack的每一个储存单位的值尽量小呢?也就是让每一次失败的深搜得出的d尽量小。那么我们有酱紫的计算公式: s l a c k [ e d g e [ i ] . v ] = m i n ( s l a c k [ e d g e [ i ] . v ] , n u m x [ x ] + n u m y [ e d g e [ i ] . v ] - e d g e [ i ] . d i s ) ,也就是每一个点的slack都等于那个因为这个原因不能匹配的那个点的权值加上当前点的权值减去这个边权。比如2和6要匹配的时候,发现2的点标和6的加起来不是1,那么2的slack就是3+0-1等于2。当然,每个点都会有自己的slack。
然后我们利用一个for循环选出slack最小的,那就是我们最终的d了。然后左边减少右边加上。
我们利用numx和numy数组存左右两边的点的点标。使用nx和ny数组存匹配关系。预处理代码如下:
#define inf 0x3f3f3f
const long long maxm=10001;
int p,s;
struct e{
int u,v,dis,next;
}edge[maxm];
int head[maxm],js;
int nx[maxm],ny[maxm];
int numx[maxm],numy[maxm];
int slack[maxm];
int l[maxm],lx;
bool visx[maxm],visy[maxm];
int a,b,c;
int d;
注意,我们使用了两个标记是否走过的vis数组(一个记录左边,一个记录右边),是因为我们最后统计出来的d是左边减,右边加。而我们仅仅减少左边走过的,增加右边走过的,所以方便一点就把vis分开两个部分记录了。
根据上图,我们的输入是酱紫(假设我们一直左边的所有点):
cin>>p>>s>>lx;
for(int i=1;i<=s;i++){
cin>>a>>b>>c;
addedge(a,b,c);
}for(int i=1;i<=lx;i++) cin>>l[i];
样例模拟
现在才正式开始讲KM算法呢!刚才都是概要,听不懂很正常。
讲完了开头和结尾以及匈牙利和KM的小小的不同点,我们现在开始正式讲讲它的实现。
那么我们在KM算法执行之前就需要先把每一个点的点标先计算出来吧。
如下代码可以计算每一个点的点标:
for(int i=1;i<=lx;i++){ //初始化给予每一个点的初始点标
for(int j=head[l[i]];j;j=edge[j].next){
numx[l[i]]=max(numx[l[i]],edge[j].dis);
}
}
这是什么意思呢?外层那个循环是枚举每一个左边的点,为什么右边的不需要呢?右边的本来就是0,所以不需要(全局变量初始默认0),内层循环是遍历当前这个点的所有出边,很熟悉吧。然后第三行才是重点,就是利用循环找出最大权值的出边。然后存到numx数组里面。
这一步走完,就会是酱紫:
![]()
KM算法和匈牙利算法有一个不同点,匈牙利算法以每一个左边的点出发作为起点的dfs每个点都只要一次,每一次只是判断有没有匹配上,没有匹配上就说明确实这个点是无法匹配的。
然而这个KM算法没有匹配上却不一定是它真的配不上,而会可能会受到点标的影响而无法匹配,所以我们需要从一个点出发深搜多次,直到找到匹配的为止。
我们每一次深搜结束都会选出最小的d并且调整点标。这就意味着每一次深搜前要做好初始化工作。把所有的vis设置0,所有的slack设置为inf。所以我们每一次dfs前可以酱紫,并且设定一个条件——只要有匹配,就去深搜下面一个点,代码如下:
memset(slack,inf,sizeof(slack));
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(dfs(l[i])) break;
为什么这里有break呢?因为我们外面还用了一个while(1),意思就是只要没有找到就一直找,找到了才break。这时候大家会问,假如这东西本来就找不到匹配的呢?那岂不是永远都退出不了循环?是的,所以我才会说开头那句话:只能是在被深搜的点本来就可以匹配的情况下才能使用。这就意味着使用KM之前你也许会需要一次匈牙利来得出所有可以匹配的点。初始化完毕就会酱紫:
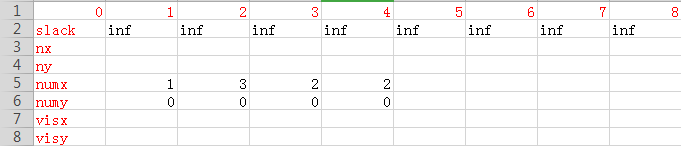
这里调用了dfs函数,所以我再花一点笔墨讲讲这个dfs函数需要怎么写。其实就是在匈牙利算法的基础上改一点点而已。我先扔个代码,你们看着代码结合我的模拟就可以弄懂。
bool dfs(int x){
visx[x]=1;
for(int i=head[x];i;i=edge[i].next){
if(numx[x]+numy[edge[i].v]==edge[i].dis){
if(!visy[edge[i].v]){
visy[edge[i].v]=1;
if(!ny[edge[i].v] || dfs(ny[edge[i].v])){
ny[edge[i].v]=x;
nx[x]=edge[i].v;
return 1;
}
}
}
//计算当前的最小减少点标(因为最后还要用for选出真正最小的)
else slack[edge[i].v]=min(slack[edge[i].v],numx[x]+numy[edge[i].v]-edge[i].dis);
}
return 0;
}
当然,第二行,搜到这个点,我们的第一个点是点1,就记录这个点搜过了对吧。接下来第三行还是那么熟悉的遍历所有出边。然而第4行我们多了一个判断:i f ( n u m x [ x ] + n u m y [ e d g e [ i ] . v ] = = e d g e [ i ] . d i s ) 这个就是判断当前找到的这个出边对应的点的点标和你目前所在的点的点标之和是否等于边权。其实就是判断i f ( n u m x [ 1 ] + n u m y [ 5 ] = = 1和5之间的边的边权 ),结果是相等。
紧接着判断点5是否搜过?啊,没有搜过。所以我们又通过了这一层判断,然后赶紧标记点5已经被搜过了。
然后我们遇到了第三个判断,这个if(!ny[edge[i].v] || dfs(ny[edge[i].v]))判断可是跟匈牙利的一毛一样了,第一个判断是否已经匹配,第二个是有匹配的话往上面的点去询问,这里不细讲,不会的看这里:
二分图最大匹配——匈牙利算法
显然点5没人匹配呢,所以匹配,如下图,红线代表被匹配了:

然后return了1,于是成功break出来。
第一轮所有数组除了vis基本没怎么变化,因为太顺利了,三个判断全都通过了。
接下来我们开始从第二个点出发寻找匹配了。
同样,memset一通,我们开始愉快的深搜!
遗憾,第二个点搜到的是点5。被i f ( n u m x [ x ] + n u m y [ e d g e [ i ] . v ] = = e d g e [ i ] . d i s ) 判断拦下了!那么这就是我说的因为点标无法匹配的情况,所以我们开始计算这个点的slack!
所以执行else语句:s l a c k [ e d g e [ i ] . v ] = m i n ( s l a c k [ e d g e [ i ] . v ] , n u m x [ x ] + n u m y [ e d g e [ i ] . v ] - e d g e [ i ] . d i s ) ,其实就是s l a c k [ 5 ] = m i n ( s l a c k [ 5 ] , n u m x [ 2 ] + n u m y [ 5 ] - 2和5的边的边权 ) ,所以s l a c k [ 5 ] =3+0-1=2。
然后我们继续深搜,然后搜到了点6,当然过不了第一层判断,也是调整点标。最后搜到了点7,这一次无需调整,成功和点7匹配了!
如果真的要调整点标的话,怎么调整呢?
我给出下面的代码,可以完美调整点标!(这段代码写在DFS的后面,参考最后的示例代码)
d=inf;
//inf是常量,不可以变化,所以用一个int暂时存着
for(int j=1;j<=p;j++){
if(!visy[p]){
d=min(d,slack[j]);
}
}
for(int j=1;j<=p;j++){
if(visy[j]) numy[j]+=d;
if(visx[j]) numx[j]-=d;
}
我们之后再讲讲这段代码有什么卵用,先上个匹配后的神图:
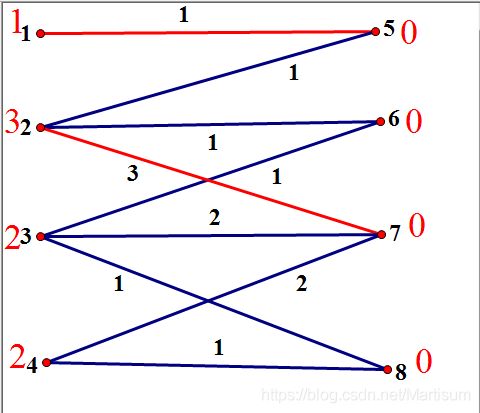
接下来是第三个点。
它搜到了点6,第一层判断过不了,调整点标,则slack[6]=1;(slack数组每次深搜前都会初始化成inf)
然后搜到了点7,高高兴兴地跟7匹配?然而它已经跟2号牵手了,怎么办?这时,我们会询问点2还可不可以匹配别人,于是根据dfs(ny[edge[i].v]),2号点又去询问5号和6号,你会问6号不是问过了么为什么还可以再问?仔细看代码哦,不管有无vis,都是可以访问的。
然后点5匹配不了,调整slack[5]=2,slack[6]=2(但是原本是1,我们d尽量取小,所以无法更新)
弄了半天,点2除了老情人7,啥子也没有匹配上,于是告诉3说,对勿起,没有啦!
于是点3也就不再想着点7,而是把目标转向了8,然而8也是个渣人,没办法——改!
所以slack[8]=1;
好了,点3遗憾退场。当然,while(1)循环是不会放过他的。
于是执行我刚刚说的那一堆代码。
注意:刚刚调整的数据是slack[6]=1,slack[5]=2,slack[8]=1
第一遍for循环只是为了找出最小的d,而且仅仅针对没有被搜过的,因为没有被搜的点恰是为我们提供slack的点,而搜过的,于是最小的d就是1。下一个循环就可以调整点标了,这里我们搜过的是3,2,7三个点。所以就调整3,2,7的点标。
左边点减去,右边的加上,所以结果就是酱紫:
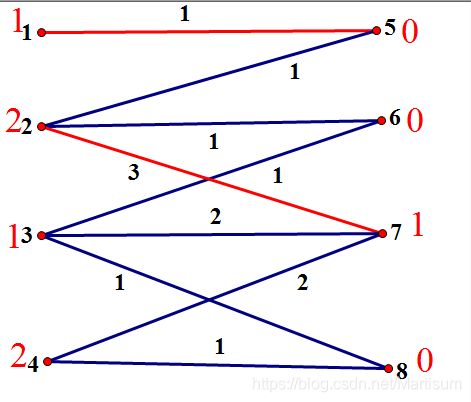
所以第二次再去匹配的时候,点3就匹配了点6了。
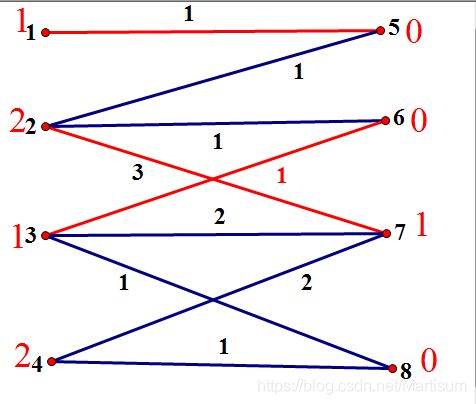
呼呼呼!
终于到最后一个点了!
点4会先找到点7,然而第一个判断就不行了,所以slack[7]=1
接着找8.于是slack[8]=1
但是仍然没有找到一个点…所以光荣退出深搜,搜到的点是4
4调整点标后就是酱紫

第二次的时候,4无法与7匹配,因为其他1,2,3实在挪不出位置了(自己思考一下),最后,4与8匹配了。

| 样例输入 | 样例输出 |
|---|---|
| 8 9 4 | 5配1 |
| 1 5 1 | 7配2 |
| 2 5 1 | 6配3 |
| 2 6 1 | 8配4 |
| 2 7 3 | |
| 3 6 1 | |
| 3 7 2 | |
| 3 8 1 | |
| 4 7 2 | |
| 4 8 1 | |
| 1 2 3 4 |
下面给出示例代码:
#include