权值线段树、主席树学习
初学主席树,主要是反复看了卿学姐的视频(我竟然在B站学算法)和知乎“主席树是如何求区间k大的”,才算懂了点皮毛。
传送门:
卿学姐的B站视频
知乎-“主席树是如何求区间k大的”
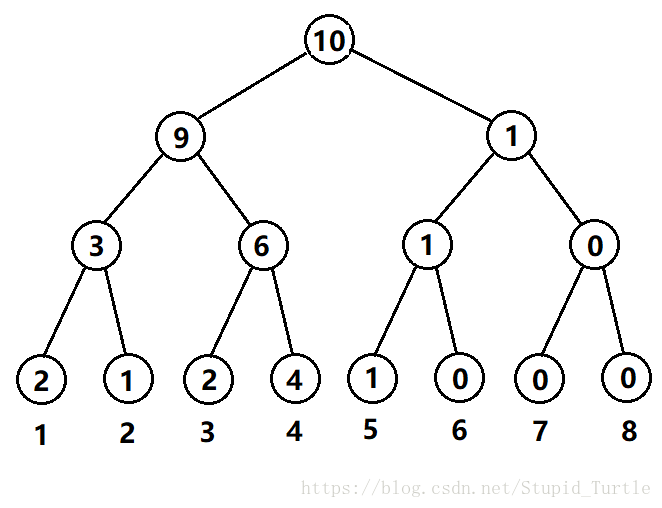
首先,学习主席树要点的前置技能是权值线段树(卿学姐说的是线段树,个人认为不太确切)。权值线段树之所以会带上“权值”二字,是因为它是记录权值的线段树。因此需要用到离散化操作来处理a[1-n]。记录权值指的是,每个点上存的是区间内的数字出现的总次数。比如一个长度为10的数组[1,1,2,3,3,4,4,4,4,5]。
其中1出现了两次,那么[1,1]这个节点的值为2,2出现了1次,那么[2,2]这个节点的值为1,那么显然[1,2]这个节点的值为3,即1出现的次数和2出现的次数加和。那么如果我想要知道这个数组上的第k小,我就可以在这棵权值线段树上用logn的时间来实现。比如我想要求这个区间上的第7小,那么我先找到这棵树的根节点,根节点上的数字显示的是10,表示在[1,8]这个区间上一共有10个数字,那么我只要去看它的左孩子上的个数是多少。这时我看到左孩子上的数字是9,说明前9小的数字都在左子树上,那么我要找的第7小也在左子树上,那么我就递归去找左子树。当我再看左孩子的时候,看到数字是3,说明前3小的数字在左子树上,那么我要找的就是右子树上的第k-sum[i]小,即7-3=4,找到右子树上的第4小即可。直到找到某一个叶子节点,说明找到了我要找的第k小。这是通过权值线段树找到区间[1,n]上的第k小/大的应用。
那么知道了权值线段树是什么之后,主席树又是什么呢。主席树是一棵可持久化线段树,可持久化指的是它保存了这棵树的所有历史版本,最简单的办法是:如果你输入了n个数,那么每输入一个数字a[i],就构造一棵保存了从a[1]到a[i]的权值线段树。之所以这么做,是因为我们可以把第j棵树和第(i-1)棵树上的每个点的权值相减,来得到一颗新的权值线段树,而这个新的权值线段树相当于是输入了a[i]到a[j]以后得到的。如果这么说不太好理解的话,我们可以思考另外一个模型:求数组a[1]到a[n]的和。如果只是求[1,n]这一段的和,那么我们直接全部加起来就可以了,或者求一个前缀和sum[n]即可。那么如果我给定了l和r,想要知道[l,r]这段区间上的和呢?是不是利用前缀和sum[r]-sum[l-1]就可以轻松得到?那么主席树的思想也是如此,将tree[r]-tree[l-1]得到的一棵权值线段树即为属于[l,r]的一棵权值线段树,那么在这么一棵权值线段树上求第k大不是就转变为之前的问题了么。如果还是没有理解为什么可以用tree[r]-tree[l-1]来表示属于[l,r]的权值线段树,可以自己构造一个数组,然后画出属于[1,l-1],[1,r]和[l,r]的三颗权值线段树,来自己研究研究,多自己动手也不是一件坏事嘛。
还有一个问题需要解决,那就是空间问题。显而易见的是,如果每输入一个数就重新构造一棵权值线段树,必然会导致空间不够用:一棵线段树的空间就是n*4,那么一共的空间开销就是n*n*4,显然是会MLE的。那么这个问题怎么解决呢?可以发现每更新一个点,就会从它开始把它的所有祖先都更新一次,而其他的点都没有被改变,即:每次改变的结点只有logn个。这样,我们每次输入一个数,只需要多开logn个空间,那么实际的空间开销只有n*(4+logn),满足了空间要求。
以两道基础题结束。(代码主要仿照卿学姐的视频中的代码)
POJ-2104
AC代码:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll ;
const int oo=0x7f7f7f7f ;
const int maxn=1e5+7;
const int mod=1e9+7;
int n,m,cnt,root[maxn],a[maxn],x,y,k;
struct node{
int l,r,sum;
}T[maxn*25];
vector v;
int getid(int x){
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void update(int l,int r,int &x,int y,int pos){
T[++cnt]=T[y],T[cnt].sum++,x=cnt;
if(l==r) return;
int mid=(l+r)/2;
if(mid>=pos) update(l,mid,T[x].l,T[y].l,pos);
else update(mid+1,r,T[x].r,T[y].r,pos);
}
int query(int l,int r,int x,int y,int k){
if(l==r) return l;
int mid=(l+r)/2;
int sum=T[T[y].l].sum-T[T[x].l].sum;
if(sum>=k) return query(l,mid,T[x].l,T[y].l,k);
else return query(mid+1,r,T[x].r,T[y].r,k-sum);
}
int main(void){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),v.push_back(a[i]);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++) update(1,n,root[i],root[i-1],getid(a[i]));
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&k);
printf("%d\n",v[query(1,n,root[x-1],root[y],k)-1]);
}
return 0;
}
HDU-2665
AC代码:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll ;
const int oo=0x7f7f7f7f ;
const int maxn=1e5+7;
const int mod=1e9+7;
int t,n,m,cnt,root[maxn],a[maxn],x,y,k;
struct node{
int l,r,sum;
}T[maxn*25];
vector v;
int getid(int x){
return lower_bound(v.begin(),v.end(),x)-v.begin()+1;
}
void update(int l,int r,int &x,int y,int pos){
T[++cnt]=T[y],T[cnt].sum++,x=cnt;
if(l==r) return;
int mid=(l+r)/2;
if(mid>=pos) update(l,mid,T[x].l,T[y].l,pos);
else update(mid+1,r,T[x].r,T[y].r,pos);
}
int query(int l,int r,int x,int y,int k){
if(l==r) return l;
int mid=(l+r)/2;
int sum=T[T[y].l].sum-T[T[x].l].sum;
if(sum>=k) return query(l,mid,T[x].l,T[y].l,k);
else return query(mid+1,r,T[x].r,T[y].r,k-sum);
}
int main(void){
scanf("%d",&t);
while(t--){
v.clear();
cnt=0;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),v.push_back(a[i]);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
for(int i=1;i<=n;i++) update(1,n,root[i],root[i-1],getid(a[i]));
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x,&y,&k);
printf("%d\n",v[query(1,n,root[x-1],root[y],k)-1]);
}
}
return 0 ;
}
之所以把hdu-2665也放上来,是因为在这道题的初始化上踩了坑,只记得把vector清空,忘记把作为存储初始值的cnt给赋为0,也算是一个提醒吧。顺带一提,hdu-2665的题意说的是求区间第k大,但是区间第k大wa了,而区间第k小AC了,很奇怪2333。