AtCoder Grand Contest 001 做题记录
欢迎回来
A - BBQ Easy
题意:有 2N 2 N 根烤肉扦,第 i i 个烤肉扦长度为 Li L i ,每一块肉需要横跨两根烤肉扦,长度为 1 1 。可以随意分配烤肉扦的顺序,询问最多同时可以烤多少块肉。
N≤100,Li≤100,Li N ≤ 100 , L i ≤ 100 , L i 是整数
解答:将烤肉扦从小到大排序,下标为奇数的位置之和即为答案。
#include B - Mysterious Light
题意:有一个边长为 N N 的正三角形,顶点分别为 a a 、 b b 、 c c ,有一束激光从 ab a b 边上,距离 a a 为 x x 的位置,平行于 bc b c 射入正三角形。激光遇到三角形的三边或者已经走过的光路时,会发生镜面反射。询问最后激光回到出发点时,走过光路的长度。
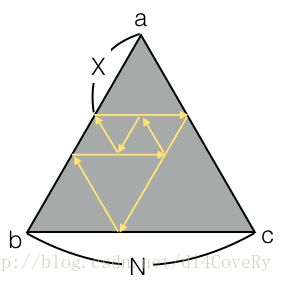
2≤N≤1012,1≤X≤N−1 2 ≤ N ≤ 10 12 , 1 ≤ X ≤ N − 1
解答:答案为 3(N−gcd(N,X)) 3 ( N − g c d ( N , X ) )
原图形走两步就会变成一个平行四边形,两边分别为 (X,N−X) ( X , N − X ) ,这两步的长度为N
考虑这样一个长宽为 a a 、 b b 平行四边形,设需要的步数为 F(a,b) F ( a , b )
那么有这样一个关系式:
若 a>b a > b , F(a,b)=F(b,a) F ( a , b ) = F ( b , a )
若 a=b a = b , F(a,b)=a=b F ( a , b ) = a = b
若 a<b a < b , F(a,b)=2a+F(b−a,b) F ( a , b ) = 2 a + F ( b − a , b )
这样我们就已经得到一个log级别的递推算法了
我们还可以对这个式子化简
我们定义 phi(F(a,b))=a+b p h i ( F ( a , b ) ) = a + b
当a ≠b ≠ b 时, phi p h i 每下降 x x , F F 的值会增加 2x 2 x
当 a=b a = b 时, phi p h i 每下降 2x 2 x , F F 的值会增加 x x
加上最开始走的两部,可以得知答案为 3(N−gcd(N,X)) 3 ( N − g c d ( N , X ) )
#include C - Shorten Diameter
题意:给定一棵 N N 个节点的树,至少移除多少个节点,使得该树的直径 ≤K ≤ K 。
2≤N≤2000 2 ≤ N ≤ 2000 ; 1≤K≤N−1 1 ≤ K ≤ N − 1 ; 1≤Ai≤N 1 ≤ A i ≤ N ; 1≤Bi≤N 1 ≤ B i ≤ N
解答:若一个树的直径小于等于 K K ,则一定存在一条边,使得删除这条边之后,以边的两个端点为根的子树深度分别小于等于 ⌈K−12⌉ ⌈ K − 1 2 ⌉ 和 ⌊K−12⌋ ⌊ K − 1 2 ⌋ 。爆枚这条边再dfs判深度即可,时间复杂度 O(N2) O ( N 2 )
#include int u = rd(), v = rd();
a[i] = u, b[i] = v;
E[u].push_back(v);
E[v].push_back(u);
}
int ans = INF;
if (k%2 == 0) {
for (int i=1;i<=n;i++) {
tot = 0;
dfs(i, i ,0);
ans = min(ans, n - tot);
}
} else {
for (int i=1;i0;
dfs(a[i], b[i], 0);
dfs(b[i], a[i], 0);
ans = min(ans, n - tot);
}
}
cout << ans << endl;
return 0;
} D - Arrays and Palindrome
题意:
给定一个长度为 M M ,和为 N N 的序列{ A A },需要重排 A A 并且构造一个数列{ B B }满足:
1、{ B B }的元素和为 N N
2、任何序列满足 (1) ( 1 ) 和 (2) ( 2 ) 的都满足 (3) ( 3 )
(1)序列的这些元素是回文串:前 A1 A 1 个项,接下来 A2 A 2 项,接下来 A3 A 3 项……
(2)序列的这些元素是回文串:前 B1 B 1 个项,接下来 B2 B 2 项,接下来 B3 B 3 项……
(3)该序列的所有元素相同
1≤N≤105 1 ≤ N ≤ 10 5
1≤M≤100 1 ≤ M ≤ 100
Ai≤105 A i ≤ 10 5
解答:
转化一下模型,有一排 N N 个点,长度为 L L 的回文串相当于连接 ⌊L2⌋ ⌊ L 2 ⌋ 条无向边,要求最后所有的点都在一个联通分量里面。
显然至少需要 N−1 N − 1 条边,那么无解的情况我们就可以通过这个来判断了。如果 A A 中的奇数项大于等于3,无解。
单独讨论一下 M=1 M = 1 的情况
当 M≥2 M ≥ 2 时,将 A A 中的奇数项移动到两端, B1=A1−1 B 1 = A 1 − 1 , BM=AM−1 B M = A M − 1 ,其余的 Bi=Ai B i = A i 即可。
#include E - BBQ Hard
题意:
给定 N N 个数{ A A }和{ B B },求
解答:
对 CAi+AjAi+Bi+Aj+Bj C A i + B i + A j + B j A i + A j 可以看做是平面直角坐标系中,从 (−Ai,−Bi) ( − A i , − B i ) 到 (Aj,Bj) ( A j , B j ) 最短路的数量。(只能从整点走到整点)
那么将每个 (−Ai,−Bi) ( − A i , − B i ) 作为起点,每个 (Ai,Bi) ( A i , B i ) 作为终点,最短路条数之和就能得到
减去 ∑ni=1CAi+Bi2(Ai+Bi) ∑ i = 1 n C 2 ( A i + B i ) A i + B i 后再除以二即可
#include F - Wide Swap
题意:
给定一个长度为 N N 的排列 P P ,对于 i i , j j 满足 j−i≥K j − i ≥ K 且 |Pi−Pj|=1 | P i − P j | = 1 就可以交换这两个元素,求字典序最的序列。
解答:
阅读和参考了官方题解以及
https://www.cnblogs.com/BearChild/p/7895719.html
令 Q Q 为 P P 的转置,即 QPi=i Q P i = i 。
由字典序的性质可得,当 Q Q 字典序最小时, P P 字典序最小。
对排列 P P ,只有在两个元素相邻并且权值差不小于 K K 时才能交换。
由此得出一个性质,当两元素 Px P x 和 Py P y ( x<y x < y )的权值差小于 K K 时,无论怎么操作 Px P x 元素始终在 Py P y 元素前面。
显然,满足所有上述限制的排列,一定能够通过合法的交换得到。
那么对于权值差小于 K K 的两个元素 Px P x 和 Py P y ,我们从 Px P x 向 Py P y 连一条边,那么一组合法解便满足该图的拓扑序。
这么连边的边数是 O(N2) O ( N 2 ) ,下面优化连边:
形如A–>B, B–>C, A–>C的连边中,A–>C这条边显然在拓扑关系中无用。
我们考虑如何避免加入 A–>C 这种边:将 Pi P i 连向 (Pi−K,Pi) ( P i − K , P i ) 和 (Pi,Pi+K) ( P i , P i + K ) 两个区间下标最小的那一个即可。线段树维护区间最小值。
时间复杂度: O(NlogN) O ( N l o g N )
#include