2018-2019 ACM-ICPC Southeastern European Regional (SEERC 2018) C Tree(level 2)(树的直径)(4种解法)
题目链接
题意:
给你一棵n个点的树(n<=100),每一个点有白/黑色,让你选m个黑色的点,
使得你选的这m个点的集合里最远的两个点的距离最小
解析:
这道题我训练的时候是用st的LCA求两点距离+二分+最大团验证来做的,代码有167行
比赛的时候...估计得写将近1个小时,然后还被自己LCA模板上的一个数组大小卡了半个小时...
这道题赛后看了大佬们的代码,大多都是和树的直径联系在一起的。
可以看一下树的直径及其证明。
里面有一个很重要的性质,就是树上一个点x最远能到达的点一定是直径的一个端点
这道题做法很多,首先一个比较简单版本的就是枚举任意两个点x,y,记录他们的距离为最长距离res
然后把剩余的点k加进来,如果dis[x][k]<=res&&dis[k][y]<=res,那么这个点就是可以加入的
如果最后的点数>=m,那么对答案进行更新
这里为什么点k满足dis[x][k]<=res&&dis[k][y]<=res就可以加入进来,保证k与集合里面的其他点的距离都<=res?
那么下面是证明
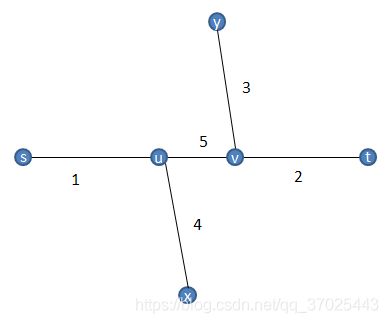
假定我们枚举的边是st,然后x,y都加入了集合
su=编号1,uv=编号5,vt=编号2,ux=编号4,vy=编号3
那么x,y加入集合条件是1+4<=1+5+2, 4+5+2<=1+5+2
=>4<5+2 && 4<=1
同理3<=5+1 && 3<=2
那么我们证明4+3+5的长度
4+3+5(xy)<= 1+3+2(st)
那么就满足了条件了
所以这个思想得到的一个结论是
一条树链xy的长度为p,,如果两个点s,t都满足dis[s/t][x]<=p&&dis[s/t][y]<=p
那么dis[s][t]一定满足<=p
代码来源于Engineering Drawing
#include
using namespace std;
const int N = 100 + 5;
vector G[N];
int dis[N][N], level[N], col[N], n, m;
void addedge(int u, int v) {
G[u].push_back(v);
G[v].push_back(u);
}
void bfs(int s) {
memset(level, -1, sizeof level);
queue q;
level[s] = 0;
q.push(s);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int v : G[u])
if(level[v] == -1) {
level[v] = level[u] + 1;
q.push(v);
}
}
for(int i = 1; i <= n; i++)
dis[s][i] = level[i];
}
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> col[i];
for(int i = 1; i <= n - 1; i++) {
int u, v; cin >> u >> v;
addedge(u, v);
}
for(int i = 1; i <= n; i++)
if(col[i]) bfs(i);
int ans = 1000;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(col[i] && col[j]) {
int cnt = 0;
for(int k = 1; k <= n; k++)
if(col[k] && max(dis[i][k], dis[j][k]) <= dis[i][j]) cnt++;
if(cnt >= m) ans = min(ans, dis[i][j]);
}
cout << ans << endl;
} 另外一种是来源于一个博客上的
先二分出一个最大距离k
他的思路就是边bfs边dfs,用bfs层次遍历
然后用bfs遍历过的点的vis[]标记重新建树
假定一开始我们以1为根,那么bfs层次遍历的时候遍历到x
x一定是距离1最远的点,距离为x的层数
那么x也一定是bfs层次遍历新建的树的直径的一个端点(叶子节点),
那么我们只需要从这个端点出发dfs(假定这个点的深度为0),深度<=k的黑点有多少
如果有>=m个,那么就返回1,否则返回0
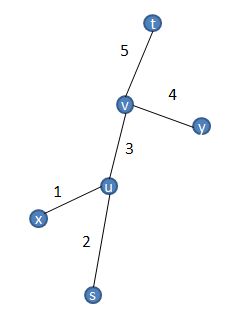
假定bfs起点是t,现在bfs遍历到s.上面是遍历到s时新建的bfs层次遍历树
su=编号2,vu=编号3,xu=编号1,vy=编号4,vt=编号5
那么从s开始dfs,假定x,y都是可以选入集合的点,即sx=1+2<=k,sy=2+3+4<=k
那么怎么保证1+3+4<=k?
有bfs层次树的性质是5+3+1<=5+3+2, 5+4<=5+3+2
=> 1<=2 , 4<=3+2
那么1+3+4(xy)<=2+3+4(sy)<=k
这个思想的结论是
从树上深度最深的点/直径的一个端点(保证该点所在的层数都>=其他点),记作s,出发dfs形成的dfs树。只要保证该dfs树上的点y到s的距离<=k(即y在s的dfs树上的深度<=k,等价于这棵dfs树的高度==k),那么这棵dfs树上任意两点的距离都<=k
#include
#define maxn 105
using namespace std;
vectorvec[maxn];
int vis[maxn];//用vis数组去区分点的不同的集合
int a[maxn];
queueque;
int n,m;
int ans=0;
int dfs(int now,int fa,int all,int dis){
int res=a[now];
if(dis==all) return res;
for(auto &it:vec[now]){
if(!vis[it]||it==fa) continue;
res+=dfs(it,now,all,dis+1);
}
return res;
}
bool check(int k){//二分的check,本质上为一个bfs
memset(vis,0,sizeof(vis));
while(!que.empty()) que.pop();
que.push(1);
while(!que.empty()){//bfs选取部分点集
int now=que.front();
que.pop();
vis[now]=1;
int tmp=dfs(now,0,k,0);//通过dfs获取这个集合的黑点的个数
if(tmp>=m) return 1;
for(auto &it:vec[now]){
if(vis[it]) continue;
que.push(it);
}
}
return 0;
}
int main()
{
//freopen("in.txt","r",stdin);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=0;i>1;
if(check(mid)) r=mid;
else l=mid+1;
//cout< 这里再将一个树形dp的版本,因为我看也有很多人是用这个过的。
二分答案的时候check用树形dp
dp[i][j]表示以i为根,到i的距离<=j的黑色节点的个数,同时保持任意两个点的距离<=md
其实就是维护一棵以i为根的树,这棵树任意两点的距离<=md,并使这棵树的黑色节点最多,
即一棵以i为根,树的高度<=j,且树上任意两点距离<=md的节点最多的黑树
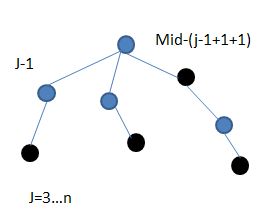
下面是转移。我们得到dp[i][j]通过三种途径转移。
1.从dp[i][j-1]转移
2.如果j-1 即从 3.如果md-1-j 距离<=md 上面都-1是因为孩子节点到父节点还有1的距离要加 那么dp[i][j]取三者之中的最大值就可以了。这个套路其实在树形dp上挺常见的 代码来源 最后放一个st的LCA求两点距离+二分+最大团,167行的代码... ![]() 转移。这样求解一个原因也源于dp[i][j]是高度<=j的最优情况,所以永远有dp[i][j]>=dp[i][k] k
转移。这样求解一个原因也源于dp[i][j]是高度<=j的最优情况,所以永远有dp[i][j]>=dp[i][k] k#include #include