用Keras实现一个DeepFM
用Keras实现一个DeepFM
本文仅提供一个思路,有问题欢迎指出,转载请注明,谢谢。
一、数据格式
在设计模型之间,首先要明确数据的格式应该是怎样的。我们假设现在要解决的问题是一个CTR预估问题,数据集是 (X,y) ( X , y ) ,每一个样本都是高度稀疏的高维向量。假设我们有两种 field 的特征,连续型和离散型,连续型 field 一般不做处理沿用原值,离散型一般会做One-hot编码。离散型又能进一步分为单值型和多值型,单值型在Onehot后的稀疏向量中,只有一个特征为1,其余都是0,而多值型在Onehot后,有多于1个特征为1,其余是0。
下面给出一个两个样本的例子,其中shop_score是连续型field,gender是单值离散型field,interest是多值离散型field。可以看到shop_score的取值是实数,gender的取值是离散值,interest的取值是离散值序列。
| label | shop_score | gender | interest |
|---|---|---|---|
| 0 | 0.2 | male | football, cooking |
| 1 | 0.8 | female | cooking |
对各field进行Onehot后,可见单值离散field对应的独热向量只有一位取1,而多值离散field对应的独热向量有多于一位取1,表示该field可以同时取多个特征值。
| label | shop_score | gender=m | gender=f | interest=f | interest=c |
|---|---|---|---|---|---|
| 0 | 0.2 | 1 | 0 | 1 | 1 |
| 1 | 0.8 | 0 | 1 | 0 | 1 |
进一步,我们对每个field中的特征取值分别单独编码或联合编码,则确定了特征的index,这在libsvm和libffm数据格式中是需要的。
| field | feature | encoding separate | encoding union |
|---|---|---|---|
| shop_score (1) | 1 | 1 | |
| gender (2) | male | 1 | 2 |
| gender (2) | female | 2 | 3 |
| interest (3) | football | 1 | 4 |
| interest (3) | cooking | 2 | 5 |
libsvm格式:
libffm格式:
可见,连续field和单值field对样本长度的贡献恒定为1,但多值离散型field可能会导致样本长度不一样。对不定长样本的处理方法自然是padding补零了,但我选择对每个多值field分别进行padding,原因有二。首先,若对样本整体进行padding,万一想要进行截断,可能会截掉某些连续field和单值field,分别padding则可以分别截断,而不影响其他的field。第二,对每个field的不同特征单独编码互不影响,不需要维护一个全局的字典,每次只需要处理一个field的特征,甚至可以实现并行处理以及节省内存的特征Encoding方案。
FM所需的数据格式正是libsvm格式,既需要数值本身(Value),也需要特征取值在字典中的index(ID)。假如我们采用对每个field的不同特征取值单独编码的方式,则可以实现一些简便性优化。首先,数值型field的ID永远是1,因此可以省略ID;第二,单值离散型field的Value永远是1,因此可以省略Value;第三,多值离散型field可以用padding+masking的方式省略ID。
给每个field分配ID和Value时,为了用0做padding,ID编码需要从1开始。如下所示,shop_score作为连续型特征,每个样本的ID和Value列表长度都是1,所有样本共用同一ID,而所有样本的Value保持原值;gender作为单值离散型field,每个样本的ID和Value列表长度都是1,ID是编码后的特征编号,由于是离散型,Value全是1;interest作为多值离散型field,ID和Value列表的长度应该取该field的最长长度,第一个样本的interestfield长度是2,因此两个样本的ID和Value列表长度都应padding补零到定长2,每个样本的ID列表是各特征取值的编码值,而Value在ID的非零位置上取1。
ID_shop_score = [[1], [1]] # 多余,可省略
Value_shop_score = [[0.2], [0.8]]
ID_gender = [[1], [2]]
Value_gender = [[1], [1]] # 多余,可省略
ID_interest = [[1,2], [2,0]]
Value_gender = [[1,1], [1,0]] # 多余,可省略根据上面给出的规则,我对各种field提取ID和Value提供参考方法如下:
- 连续型field
- ID:
np.ones()或舍弃 - Value : 沿用原 ndarray
- ID:
- 单值离散型field
- ID:
sklearn.preprocessing.LabelEncoder() - Value:
np.ones()或舍弃
- ID:
- 多值离散型field
- ID:
sklearn.preprocessing.LabelEncoder()+ padding + 加一 - Value:
np.ones()+ padding 或舍弃
- ID:
二、一个DeepFM需要哪些模块
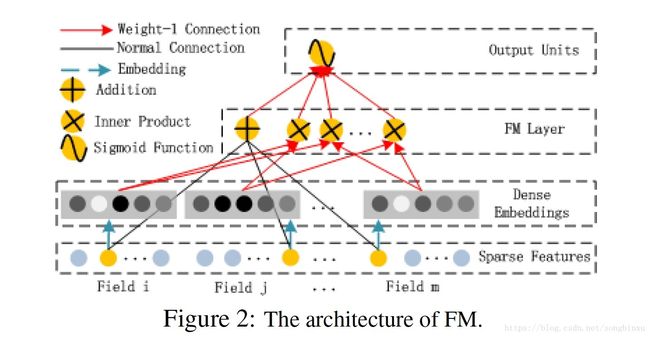
在动手写代码之前,先要对模型结构做一个宏观地观察,看看具体要实现哪些模块。上图是DeepFM论文中给出的整体网络结构图,可见要实现一个DeepFM,实现两个部分即可:FM部分和DNN部分,FM又可以进一步分为一次项和二次项。
从根源上,DeepFM的各模块共享同一输入,输入是由各个field的Onehot编码横向拼接而成的高维稀疏向量。首先,原始输入的各个field经过加权(实际上是Embedding为1维)后,求和可得一次项;其次,原始输入的各个field(不同长度)的Embedding(等长, k k 维latent vector),一方面两两内积,然后求和可得二次项,另一方面作为输入全连接到DNN。
三、Keras实现
FM部分
3.1 如何用Embedding实现 FM一次项 ∑wixi ∑ w i x i
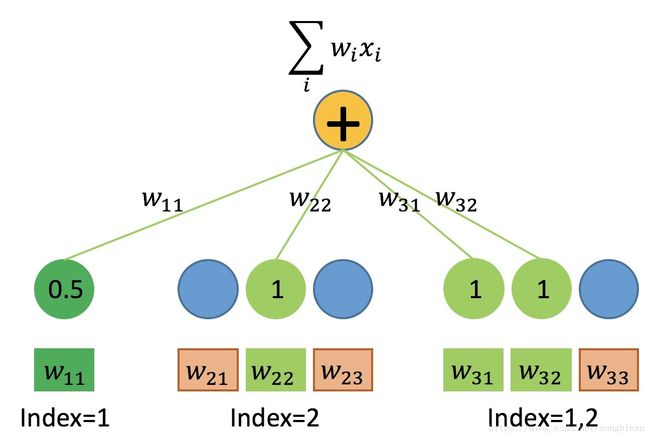
画个图分析一下,如上所述,我们的输入数据有三种field,在One-hot处理后代入FM一次项的公式运算。每个field各有一个权值向量 w w ,连续型field的 w w 长度为1,离散型field的 w w 长度为特征的取值个数。
首先,连续型field对一次项的贡献等于自身数值乘以权值 w w ,可以用Dense(1)层实现,任意个连续型field输入到同一个Dense层即可,因此在数据处理时,可以先将所有连续型field拼成一个大矩阵,同时如上所述,ID可以省略。
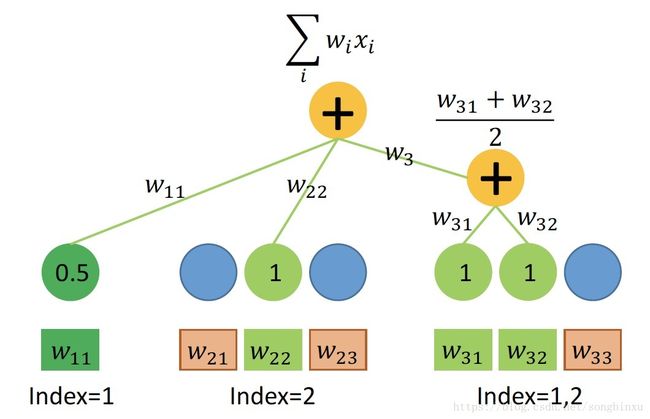
其次,单值离散型field根据样本特征取值的index,从 w w 中取出对应权值(标量),由于离散型特征值为1,故它对一次项的贡献即取出的权值本身。取出权值的过程称为 table-lookup,可以用Embedding(n,1)层实现( n n 为该field特征取值个数)。若将所有单值离散型field的特征值联合编码,则可使用同一个Embedding Table进行lookup,不需要对每个field单独声明Embedding层。因此在数据处理时,可以先将所有单值离散型field拼起来并联合编码,同时如上所述,Value可以省略,只关心lookup出来的权值 w w 即可。
最后,多值离散型field可以同时取多个特征值,为了batch training,必须对样本进行补零padding。相似地可用Embedding层实现,Value并不是必要的,但Value可以作为mask来使用,当然也可以在Embedding中设置mask_zero=True。
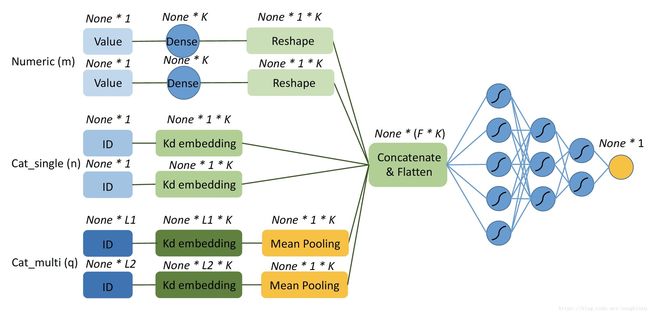
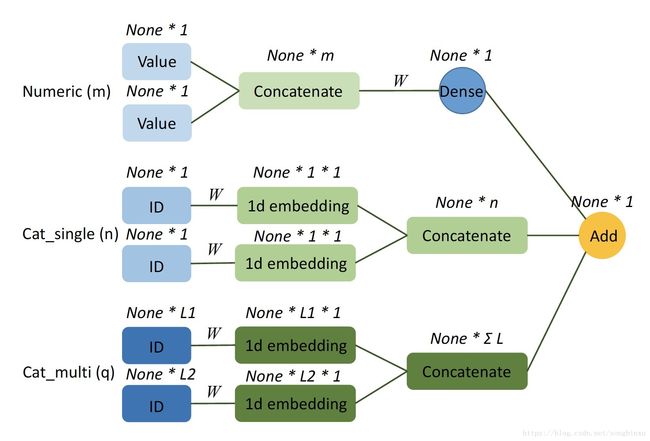
如下图所示,假设我们有 m m 个连续型field, n n 个单值离散型field, q q 个多值离散型field,每个多值离散型field的最长长度为 Li(i=1,2,⋯,q) L i ( i = 1 , 2 , ⋯ , q ) 。
网络实现
MyMeanPool
其功能是对2d或3d的tensor,指定一个axis进行求均值。例如[100,5,6]的矩阵,指定axis=1求均值,会变成[100,6]大小的矩阵。
from keras import backend as K
from keras.engine.topology import Layer
import tensorflow as tf
class MyMeanPool(Layer):
def __init__(self, axis, **kwargs):
self.supports_masking = True
self.axis = axis
super(MyMeanPool, self).__init__(**kwargs)
def compute_mask(self, input, input_mask=None):
# need not to pass the mask to next layers
return None
def call(self, x, mask=None):
if mask is not None:
if K.ndim(x)!=K.ndim(mask):
mask = K.repeat(mask, x.shape[-1])
mask = tf.transpose(mask, [0,2,1])
mask = K.cast(mask, K.floatx())
x = x * mask
return K.sum(x, axis=self.axis) / K.sum(mask, axis=self.axis)
else:
return K.mean(x, axis=self.axis)
def compute_output_shape(self, input_shape):
output_shape = []
for i in range(len(input_shape)):
if i!=self.axis:
output_shape.append(input_shape[i])
return tuple(output_shape)Network Codes
# coding:utf-8
from keras.layers import *
from keras.models import Model
from MyMeanPooling import MyMeanPool
from keras.utils import plot_model
'''Input Layers'''
# numeric fields
in_score = Input(shape=[1], name="score") # None*1
in_sales = Input(shape=[1], name="sales") # None*1
# single value categorical fields
in_gender = Input(shape=[1], name="gender") # None*1
in_age = Input(shape=[1], name="age") # None*1
# multiple value categorical fields
in_interest = Input(shape=[3], name="interest") # None*3, 最长长度3
in_topic = Input(shape=[4], name="topic") # None*4, 最长长度4
'''First Order Embeddings'''
numeric = Concatenate()([in_score, in_sales]) # None*2
dense_numeric = Dense(1)(numeric) # None*1
emb_gender_1d = Reshape([1])(Embedding(3, 1)(in_gender)) # None*1, 性别取值3种
emb_age_1d = Reshape([1])(Embedding(10, 1)(in_age)) # None*1, 年龄取值10种
emb_interest_1d = Embedding(11, 1, mask_zero=True)(in_interest) # None*3*1
emb_interest_1d = MyMeanPool(axis=1)(emb_interest_1d) # None*1
emb_topic_1d = Embedding(22, 1, mask_zero=True)(in_topic) # None*4*1
emb_topic_1d = MyMeanPool(axis=1)(emb_topic_1d) # None*1
'''compute first order'''
y_first_order = Add()([dense_numeric,
emb_gender_1d,
emb_age_1d,
emb_interest_1d,
emb_topic_1d]) # None*1
'''define model'''
model = Model(inputs=[in_score, in_sales,
in_gender, in_age,
in_interest, in_topic],
outputs=[y_first_order])
'''plot model'''
plot_model(model, 'model.png', show_shapes=True)3.2 如何用Embedding实现FM二次项 ∑∑(vi⋅vj)⋅xixj ∑ ∑ ( v i ⋅ v j ) ⋅ x i x j
由于FM的二次项是不同特征之间的交叉(一般是不同field之间的交叉),不能分field实现,必须将每个field输入Embedding后拼接起来,再求二次项。
在写代码之前,我们化简一下FM的二次项,减少一点计算复杂度。可以化简也是FM的一个优点,像FFM就做不到了。
假设 V V 矩阵大小是 [max_feat, K], X X 矩阵大小是 [batch_size, max_len],则先求Embedding VX V X ,大小为 [batch_size, F, K](这里的F是所有field拼接后的最长长度)。求和项内部第一项 (∑di=1vi,fxi)2 ( ∑ i = 1 d v i , f x i ) 2 ,即Embedding先在第1维求和变成[batch_size, K],然后逐元素求平方(还是[batch_size, K]);第二项 ∑di=1(vi,fxi)2 ∑ i = 1 d ( v i , f x i ) 2 是Embedding先逐元素求平方(还是[batch_size, F, K]),再对第一维求和,变成[batch_size, K]。两项相减之后除以2,对第1维求和,变成[batch_size, 1],即各样本二次项的值。
如图中所示,维度为1的连续型field要Embedding成 K K 维,只需使用Dense(K)层即可。维度为1的单值离散型field则用Embedding(output_dim=K)层即可。维度为 Li L i 的多值离散型field做Embedding成 K K 维,在Embedding(output_dim=K)之后,还要对axis=1做meanpooling,将Embedding平均。
网络实现
MySumLayer
from keras import backend as K
from keras.engine.topology import Layer
import tensorflow as tf
class MySumLayer(Layer):
def __init__(self, axis, **kwargs):
self.supports_masking = True
self.axis = axis
super(MySumLayer, self).__init__(**kwargs)
def compute_mask(self, input, input_mask=None):
# do not pass the mask to the next layers
return None
def call(self, x, mask=None):
if mask is not None:
# mask (batch, time)
mask = K.cast(mask, K.floatx())
if K.ndim(x)!=K.ndim(mask):
mask = K.repeat(mask, x.shape[-1])
mask = tf.transpose(mask, [0,2,1])
x = x * mask
if K.ndim(x)==2:
x = K.expand_dims(x)
return K.sum(x, axis=self.axis)
else:
if K.ndim(x)==2:
x = K.expand_dims(x)
return K.sum(x, axis=self.axis)
def compute_output_shape(self, input_shape):
output_shape = []
for i in range(len(input_shape)):
if i!=self.axis:
output_shape.append(input_shape[i])
if len(output_shape)==1:
output_shape.append(1)
return tuple(output_shape)Network Codes
# coding:utf-8
from keras.layers import *
from keras.models import Model
from MyMeanPooling import MyMeanPool
from MySumLayer import MySumLayer
from keras.utils import plot_model
'''Input Layers'''
# numeric fields
in_score = Input(shape=[1], name="score") # None*1
in_sales = Input(shape=[1], name="sales") # None*1
# single value categorical fields
in_gender = Input(shape=[1], name="gender") # None*1
in_age = Input(shape=[1], name="age") # None*1
# multiple value categorical fields
in_interest = Input(shape=[3], name="interest") # None*3, 最长长度3
in_topic = Input(shape=[4], name="topic") # None*4, 最长长度4
latent = 8
'''Second Order Embeddings'''
emb_score_Kd = RepeatVector(1)(Dense(latent)(in_score)) # None * 1 * K
emb_sales_Kd = RepeatVector(1)(Dense(latent)(in_sales)) # None * 1 * K
emb_gender_Kd = Embedding(3, latent)(in_gender)
emb_age_Kd = Embedding(10, latent)(in_age)
emb_interest_Kd = Embedding(11, latent, mask_zero=True)(in_interest) # None * 3 * K
emb_interest_Kd = RepeatVector(1)(MyMeanPool(axis=1)(emb_interest_Kd)) # None * 1 * K
emb_topic_Kd = Embedding(22, latent, mask_zero=True)(in_topic) # None * 4 * K
emb_topic_Kd = RepeatVector(1)(MyMeanPool(axis=1)(emb_topic_Kd)) # None * 1 * K
emb = Concatenate(axis=1)([emb_score_Kd,
emb_sales_Kd,
emb_gender_Kd,
emb_age_Kd,
emb_interest_Kd,
emb_topic_Kd]) # None * 9 * K
'''compute'''
summed_features_emb = MySumLayer(axis=1)(emb) # None * K
summed_features_emb_square = Multiply()([summed_features_emb,summed_features_emb]) # None * K
squared_features_emb = Multiply()([emb, emb]) # None * 6 * K
squared_sum_features_emb = MySumLayer(axis=1)(squared_features_emb) # Non * K
sub = Subtract()([summed_features_emb_square, squared_sum_features_emb]) # None * K
sub = Lambda(lambda x:x*0.5)(sub) # None * K
y_second_order = MySumLayer(axis=1)(sub) # None,
model = Model(inputs=[in_score, in_sales,
in_gender, in_age,
in_interest, in_topic],
outputs=[y_second_order])
plot_model(model, 'model.png', show_shapes=True)3.3 如何实现一个DNN
DNN从FM二次项倒数第二步生成的 None*F*K Embedding 张量开始,先用Flatten层平铺,然后经过若干层神经网络,每一层后面可以加上dropout防止过拟合和BatchNormalization加速收敛。
实现
MyFlatten
原始的Keras.layers.Flatten不支持masking,可参考我的另一篇博客。
from keras import backend as K
from keras.engine.topology import Layer
import tensorflow as tf
import numpy as np
class MyFlatten(Layer):
def __init__(self, **kwargs):
self.supports_masking = True
super(MyFlatten, self).__init__(**kwargs)
def compute_mask(self, inputs, mask=None):
if mask==None:
return mask
return K.batch_flatten(mask)
def call(self, inputs, mask=None):
return K.batch_flatten(inputs)
def compute_output_shape(self, input_shape):
return (input_shape[0], np.prod(input_shape[1:]))Network Codes
...
'''deep parts'''
y_deep = MyFlatten()(emb) # None*(6*K)
y_deep = Dropout(0.5)(Dense(128, activation='relu')(y_deep))
y_deep = Dropout(0.5)(Dense(64, activation='relu')(y_deep))
y_deep = Dropout(0.5)(Dense(32, activation='relu')(y_deep))
y_deep = Dropout(0.5)(Dense(1, activation='relu')(y_deep))
model = Model(inputs=[in_score, in_sales,
in_gender, in_age,
in_interest, in_topic],
outputs=[y_deep])
plot_model(model, 'model.png', show_shapes=True)3.4 完整的DeepFM
实现
...
'''deepFM'''
y = Concatenate(axis=1)([y_first_order, y_second_order,y_deep])
y = Dense(1, activation='sigmoid')(y)
model = Model(inputs=[in_score, in_sales,
in_gender, in_age,
in_interest, in_topic],
outputs=[y])
plot_model(model, 'model.png', show_shapes=True) DeepFM的各个部分分别实现好之后,剩下的就简单多了。
完整的代码我放在了https://github.com/SongDark/DeepFM_keras.
总结与说明
本文介绍了如何用Keras实现一个DeepFM,写完这部分代码花了我不少时间,网络并不复杂,但我一开始把问题复杂化了,写完之后发现有部分结构是多余的,又回炉重写。此外,有一些骚操作Keras不支持,例如支持masking的求和与求均值,这些都要自己重新实现,好在Keras自定义层比较简单。
这个版本的代码只是提供一种思路,它肯定不是最优的,还可以继续优化。它最大的缺点就是对每一个field都要定义对应的Input层和Embedding层,假如有100个field,代码看起来会非常冗长,很糟糕。
代码完成后我的收获有以下几点,首先,即使论文看起来很简单,但实现起来却有很多坑,有些坑你不亲自跳进去是发现不了的。第二,要善于查API,Keras只是一个框架而已,本质上和tensorflow、pytorch一样都是攻击,它还有很大的自由发展的空间。第三,要善于化简,比如离散型field对目标的贡献就是权值本身,二次项的计算可以化简等等。第四,要常做总结和记录,比如这篇博客事实上就属于实验记录的性质。第五,画图帮助理解。
最后,我感觉DeepFM虽然有深度部分,但它仍然偏向于处理离散型特征,因为我在尝试加入归一化后的连续型特征后,模型效果变差了。
本文仅提供一个思路,有问题欢迎指出,转载请注明,谢谢。
参考资料
【论文】DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
【代码】LB:0.08425 Bonne chance 系列之 NN embeding(Keras实现的部分PNN)
【API】Keras中文文档
【博客】在Keras模型中使用预训练的词向量
【博客】TensorFlow Estimator of Deep CTR-DeepFM/NFM/AFM/FNN/PNN 知乎
【问题】Mean or max pooling with masking support in Keras
【博客】因子分解机(libffm+xlearn)
【博客】深入FFM原理与实践(美团)
【API】Keras序列预处理
【github】陈成龙 DeepFM(基于tensorflow)
【github】CTR中的DNN
【github】TensorFlow Estimator of Deep CTR