数据库系统概论课堂笔记-规范化理论4

一、关系模式分解-无损连接性的判断

方法一：无损连接定理

关系模式R(U，F)的一个分解，ρ={R1,R2}具有无损连接的充分必要条件是：
U1∩U2→U1-U2 ∈F+ 或U1∩U2→U2 -U1∈F+

方法二：算法

ρ={R1,R2,...,Rk}是关系模式R的一个分解，U={A1,A2,...,An}，F={FD1,FD2,...,FDp}，并设F是一个最小依赖集，记FDi为Xi→Alj，其步骤如下：

① 建立一张n列k行的表，每一列对应一个属性，每一行对应分解中的一个关系模式。若属性Aj ∈Ui，则在j列i行填上aj，否则填上bij；

② 对于每一个FDi做如下操作：找到Xi所对应的列中具有相同符号的那些行。考察这些行中li列的元素，若其中有aj，则全部改为aj，否则全部改为bmli，m是这些行的行号最小值。

方法二例子：

   例子1（不是无损连接）：对于属性集ABCDEF和函数依赖集{A→BC，CD→E，B→D，BE→F，EF→A}，说明下列分解a.是否是无损连接分解；

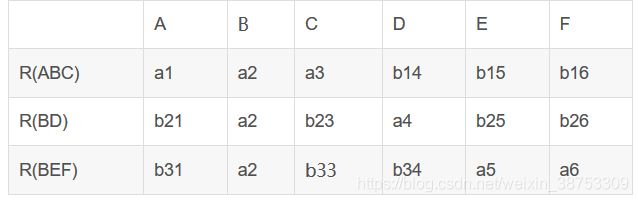
(1){ABC，BD，BEF}
a.判断无损连接分解
①构造一个初始的二维表，若“属性”属于“模式”中的属性，则填aj，否则填bij。

②根据A→BC，拆分为A→B，A→C。由于属性列A上没有相同的分量，所以表不改变。
③根据CD→E，由于属性列CD上没有相同的分量，所以表不改变。
④根据B→D，由于属性列B上第1、2、3行均相同a2，且这些行所在的D属性列存在a4，所以将属性列D上的b14、b34改为同一个符号a4。

⑤根据BE→F，由于属性列BE上没有相同的分量，所以表不改变。
⑥根据EF→A，由于属性列EF上没有相同的分量，所以表不改变。

经过比较扫描前后的表格有变化，所以进行第二次扫描，第二次扫描表无变化，没有出现a1，a2，a3，a4，a5，a6，因此不是无损连接分解。

  例子2（是无损连接）：已知R，U={A,B,C,D,E}，F={A→C,B→C,C→D,DE→C,CE→A}，R的一个分解为R1(AD)，R2(AB)，R3(BE)，R4(CDE)，R5(AE)，判断这个分解是否具有无损连接性。

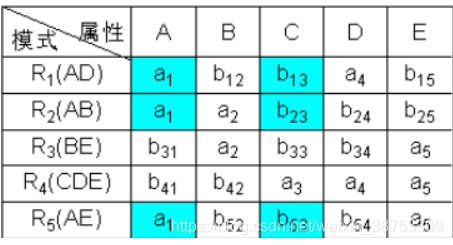
 ① 构造一个初始的二维表，若“属性”属于“模式”中的属性，则填aj，否则填bij

② 根据A→C，对上表进行处理，由于属性列A上第1、2、5行相同均为a1，所以将属性列C上的b13、b23、b53改为同一个符号b13（取行号最小值）。

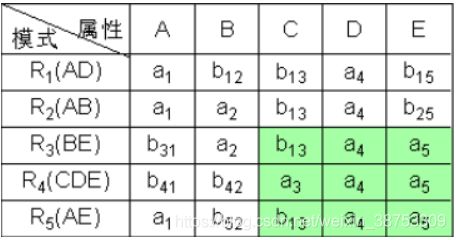
③ 根据B→C，对上表进行处理，由于属性列B上第2、3行相同均为a2，所以将属性列C上的b13、b33改为同一个符号b13（取行号最小值）。

④ 根据C→D，对上表进行处理，由于属性列C上第1、2、3、5行相同均为b13，所以将属性列D上的值均改为同一个符号a4。

   注意这里为什么改成a4？因为在四个相同的行中，存在a4，所以D的四行全部改成a4。

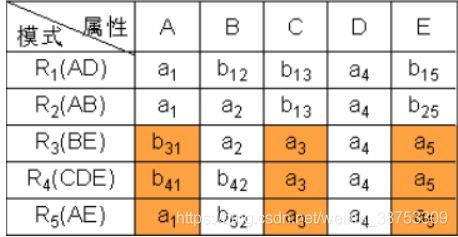
⑤ 根据DE→C，对上表进行处理，由于属性列DE上第3、4、5行相同均为a4a5，所以将属性列C上的值均改为同一个符号a3。

⑥ 根据CE→A，对上表进行处理，由于属性列CE上第3、4、5行相同均为a3a5，所以将属性列A上的值均改为同一个符号a1。

⑦ 通过上述的修改，使第三行成为a1a2a3a4a5，则算法终止。且分解具有无损连接性。

二、关系模式分解-是否保持函数依赖性的判断

定理：若F+=F1+∪F2+∪...∪Fk+，则R的分解ρ={R1，R2，...，Rk}保持函数依赖。

例题：对于属性集ABCDEF和函数依赖集{A→BC，CD→E，B→D，BE→F，EF→A}，说明下列分解b.是否保持函数依赖
b.判断保持函数依赖
U1=ABCD，F1+={A→BC，B→D}
U2=EFA，F2+={EF→A}

注：这里的F1+和F2+一定是相对于U1和U2的函数依赖集，并且依赖子句是来自于F依赖集。
丢失了CD→E，BE→F，因此没有保持函数依赖。