【混合波束成形论文阅读】基于MMSE准则的混合波束成形算法

前言

论文题目： Hybrid Beamforming for Millimeter Wave Systems Using the MMSE Criterion
论文地址：https://arxiv.org/abs/1902.08343
源码地址：https://github.com/TianLin0509/Hybrid-Beamforming-for-Millimeter-Wave-Systems-Using-the-MMSE-Criterion

这是笔者自己发表在TCom ( IEEE Transactions on Communications) 上的论文， 因为这几天要做一些相关报告，顺便也写成一篇博客。 毕竟完成了那么多篇他人论文的读后感， 也是时候记录下自己的工作了。 何况最懂一篇文章的，一定是作者本人啦。 本博文旨在以最简练的篇幅来提炼文章的核心。

背景简介

本文的工作还是基于毫米波的混合波束成形系统。 关于混合波束成形 的 背景 和 介绍， 可以参考笔者之前的文章，

• 混合波束成形专栏|基础：深入浅出5G，毫米波，大规模MIMO与波束赋形
• 混合波束成形专栏|进阶：深入浅出混合波束赋形

这篇文章与之前相关工作的主要区别点在于， 是以MSE为目标提出了一系列优化算法。 尽管在此之前已经有一些以MSE为优化目标的波束成形算法的设计工作， 但基本是多用户场景下， 且并未详尽地阐述该目标的意义。 从算法角度而言， 本文的算法也将性能优化了许多。

问题建模

本文可以分为两部分， 第一部分以上图所示的窄带点对点毫米波通信系统为研究对象， 提出了相关算法。 第二部分则将其拓展到了宽带OFDM系统下。 阅读完 混合波束成形专栏|进阶：深入浅出混合波束赋形 的话， 很容易可以写出接收端得到的接收信号的表示式：

$$\mathbf{y}={\mathbf{W}}_{\mathrm{B}}^H{\mathbf{W}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{B}}\mathbf{s}+{\mathbf{W}}_{\mathrm{B}}^H{\mathbf{W}}_{\mathrm{R}\mathrm{F}}^H\mathbf{u}$$

与许多相关工作不同的是， 本文是以MSE作为优化目标：
$$\mathrm{M}\mathrm{S}\mathrm{E}\triangleq E\left\{{\Vert {\beta }^{-1}\mathbf{y}-\mathbf{s}\Vert }^2\right\}$$

这里需要解释一下：严格的MSE应该就是 $\mathrm{M}\mathrm{S}\mathrm{E}\triangleq E\left\{{\Vert \mathbf{y}-\mathbf{s}\Vert }^2\right\}$， 而这里的$\beta$则是一个标量因子， 物理意义上是将接收到的信号放大/缩小一定的幅度， 使之更接近于原始信号。 这个MSE也被称为 modified MSE。 可以理解为用于矫正由于预编码及信道造成的信号幅度的放大/缩小。
但事实上， 因为我们研究的点对点系统中， 接收端也有波束成形操作， 因此这一步的标量scaling其实可以由接收波束赋形来完成。 那$\beta$的意义在哪里呢？ 这其实是有相应考虑的， 这并非本文的贡献， 因为传统的波束成形也会面临同样的疑问， 但这是本文需要解答的， 引入$\beta$主要出于三点考虑：

• 第一， 在传统的MIMO波束成形研究中， 在设计预编码矩阵的时候， 如果以原始的MSE（无$\beta$）为目标， 会发现预编码矩阵的设计与噪声能量无关！ 这其实不符合MSE的初衷。 而如果引入$\beta$， 预编码矩阵的解就与噪声能量相关， 也因此可以达到更合理的性能。
• 第二， 从数学意义上而言， 混合波束成形问题中，需要求解四个矩阵，愈发复杂。 而以传统MSE为目标求解的时候， 考虑发送的功率约束， 需要引入拉格朗日乘子， 这个乘子非常难求，且影响后续对其他矩阵的设计。 而引入$\beta$后， 后面的推导会证明大大简化了数学求解难度。
• 第三， 引入$\beta$后， 可以使得 固定接收端解发送端 和 固定发送端解接收端 两个子问题可以化为完全一致的形式， 也就可以用同样的算法来求解了。

最后，为什么要以MSE为目标求解， 而不是用Rate等呢？ 因为在传统通信中， MSE是一个经典且合理的指标， 完全有理由同样应用在5G的毫米波通信中。 其次， MSE为目标往往能保证更好的BER性能， 而且由于目标的不同， 数学问题完全不一样了， 推导的算法也会有较大的变化。 最后， 我们可以将MSE的算法推广到WMSE(weight MSE), 这时的解将会有非常不错的Rate性能。

波束成形设计： 数字波束成形

如 混合波束成形专栏|进阶：深入浅出混合波束赋形 中所述，在求解HBF优化问题的时候， 由于总共有4个矩阵， 主流的做法都是， 将发送端和接收端解耦， 其实就是简单的： 先固定接收端求解发送端， 再固定发送端求解接收端， 然后迭代。 我们的第一步也是如此： 先固定接收端， 求解发送端。 首先令${\mathbf{V}}_{\mathrm{B}}=\beta {\mathbf{V}}_{\mathrm{U}}$， 可以得到目标函数：

$$\begin{array}{ll}{\mathrm{minimize}}_{{\mathbf{V}}_{\mathrm{R}\mathrm{F}},{\mathbf{V}}_{\mathrm{U}},\beta }& \mathrm{tr}({\mathbf{H}}_1^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{U}}{\mathbf{V}}_{\mathrm{U}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1-{\mathbf{H}}_1^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{U}}-{\mathbf{V}}_{\mathrm{U}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1+{\sigma }^2{\beta }^{-2}{\mathbf{W}}^H\mathbf{W}+{\mathbf{I}}_{N_{\mathrm{a}}})\\ \text{ subject to }& \mathrm{tr}\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{U}}{\mathbf{V}}_{\mathrm{U}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H\right)\le {\beta }^{-2};\left|{\left[{\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right]}_{ij}\right|=1,\forall i,j\end{array}$$

可以看到， 这一步中我们只需要优化发送预编码矩阵 （数字阵和模拟阵）及 引入的$\beta$标量。 由于模拟阵有恒模约束，求解困难， 因此我们先求解数字阵。

很容易通过反证法得知： 必在达到最大功率时达到最佳性能， 因此根据第一个限制条件的等号成立时：

$$\beta ={\left(\mathrm{tr}\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{U}}{\mathbf{V}}_{\mathrm{U}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H\right)\right)}^{-\frac{1}{2}}$$

再用拉格朗日乘子法， 求解上面的问题， 利用KKT法则， 就可以求得数字阵的闭式解：
$${\mathbf{V}}_{\mathrm{U}}={\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1{\mathbf{H}}_1^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}+{\sigma }^{2}w{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)}^{-1}{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1$$
一些符号的具体定义可以找一下论文的对应， 这里就不再赘述了。 而将解得的${\mathbf{V}}_{\mathrm{U}}$代入目标函数中后， 目标函数就转化成了只和${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$相关的单变量函数了：
$$J\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)\triangleq \mathrm{tr}\left({\left({\mathbf{I}}_{{\mathrm{N}}_{\mathrm{e}}}+\frac{1}{{\sigma }^{2}w}{\mathbf{H}}_1^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)}^{-1}{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1\right)}^{-1}\right)$$
但是注意， ${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$是有恒模约束的， 因此需要设计特定的算法求解。

波束成形设计： 模拟波束成形

接上一节， 本文给出了两种算法来求解${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$

流形优化

也叫黎曼优化。 本质上是一种梯度下降法， 然而基本的梯度下降法是在整个欧式空间中进行下降， 因此无法保证下降后的解仍满足 恒模约束， 所以无法直接用于求解${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$。 而流形优化， 则是首先将满足恒莫约束的所有可行解表示为一个流形， 其后每步迭代后都将解映射回这个流形之上， 也因此可以确保结果永远满足恒模约束。 最重要的是， 已经有严谨的数学证明了这样的迭代过程是严格收敛的， 因此可以将 流形优化 理解为 在可行集上进行下降的梯度下降法。

这里推荐大家去看

• X. Yu, J. Shen, J. Zhang, and K. B. Letaief, “Alternating minimization algorithms for hybrid precoding in millimeter wave MIMO systems,” IEEE J. Sel. Topics Signal Process., vol. 10, no. 3, pp. 485-500, Apr. 2016.
  本文是借鉴和套用了他们工作提出的MO算法。 区别在于，我们的目标函数不同， 也因此得到了不同的性能。 因为我们的目标函数更复杂也更直接一些（直接以MSE为目标），因此会有更好的性能。 要想使用流形优化， 你需要求解目标问题的梯度， 然后就可以在这个框架下用下降法求出一个解了。 感兴趣的读者可以看一下这篇引文和我的paper， 基本就清楚MO的用法了。

GEVD算法

MO算法的性能卓绝， 但是复杂度偏高， 因此这里提出了一个低复杂度的算法 —— 基于GEVD（广义特征分解）。 首先， 基于一个常用的近似关系${\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}\approx N_{\mathrm{t}}{\mathbf{I}}_{N_{\mathrm{R}\mathrm{F}}}$，我们可以简化下目标函数：
$$J\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)\approx \mathrm{tr}\left({\left({\mathbf{I}}_{N_{\mathrm{e}}}+\frac{1}{{\sigma }^{2}w{N}_{\mathrm{t}}}{\mathbf{H}}_1^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_1\right)}^{-1}\right)$$
但这个问题还是非常难以求解， 因此我们提出了一种思路：固定${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$中的其余列， 每次迭代只优化1列。 通过数学变换， 我们可以把问题转化为一个GEVD问题， 并直接通过广义特征分解，得到那一列的最优解。 经过多次迭代后， 就可以得到一个不错的${\mathbf{V}}_{\mathrm{R}\mathrm{F}}$。详细的推导也见paper。 需要指出的是， 在这个求解过程中， 我们暂时忽略了恒模约束， 因此事实上，我们每次通过特征分解得到一列解之后， 需要对每个元素做一个模归一操作（相位提取）。 这一步没有任何的收敛性可言， 因此， 这个算法相比于MO算法， 没有严谨的收敛证明。然而幸运的是， 在仿真中他还是表现出了随着迭代单调下降的特性。

波束成形设计： 接收端

使用MSE为目标的另一妙处就是， 你会发现固定发送端，求解接收端的时候， 问题形式好发送端的形式一模一样。 因此，我们可以直接套用发送端的算法，用于接收端的求解，而无需额外设计了。 通过发送端和接收端的相互迭代， 最终就可以得到一组性能优异的解。

拓展到宽带系统

宽带系统，现在主流一般指的就是OFDM系统了。

系统框图如图所示。 对于数字波束成形而言， 可以对每个子载波进行设计， 因此从每个子载波来看，和窄带系统没有任何区别。 但是问题就在于模拟波束成形， 是对于所有子载波一致的。 也因此，我们设计的时候需要的不是将某个子载波上的MSE最小化的模拟阵，而是一个可以将sum-MSE最小化的解， 那么问题就变成：
$$\begin{array}{cl}\underset{{\mathbf{V}}_{\mathrm{B},k},{\mathbf{V}}_{\mathrm{R}\mathrm{F}},{\mathbf{W}}_{\mathrm{U},k},{\mathbf{W}}_{\mathrm{R}\mathrm{F}},{\beta }_k}{\text{ mibject to }}& {\sum }_{k=0}^{N-1}{\mathrm{M}\mathrm{S}\mathrm{E}}_k\\ \text{ subject to }& {\Vert {\mathbf{V}}_k\Vert }_F^2\le 1\\ & {\Vert {\mathbf{V}}_{\mathrm{R}\mathrm{F}}]}_{ij}\mid =1,\forall i,j\\ & \left|{\left[{\mathbf{W}}_{\mathrm{R}\mathrm{F}}\right]}_{ml}\right|=1,\forall m,l\end{array}$$

数字波束成形的求解和窄带一样——因为可以按每个子载波单独设计， 这里直接列出结果：
$${\mathbf{V}}_{\mathrm{U},k}={\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_{1,k}{\mathbf{H}}_{1,k}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}+{\sigma }^2{w}_k{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)}^{-1}{\mathbf{V}}_{\mathrm{R}\mathrm{F}}^H{\mathbf{H}}_{1,k}$$
接下来还是对模拟波束成形的设计。
首先，流形优化算法可以很简单的拓展到宽带场景，本来难点就在于梯度的求解，但利用下式：
$$\nabla J\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)=\sum _{k=0}^{N-1}\nabla J_k\left({\mathbf{V}}_{\mathrm{R}\mathrm{F}}\right)$$
而$\nabla J_k$的表示式和窄带是一样的推导。 有了梯度， 那么流形优化算法仍能应用。
然而GEVD算法就没法简单的拓展了， 因此， 本文提出了基于特征值分解的EVD算法。 复杂的目标显然无法直接使用EVD求解， 所以需要进行一些近似。 我们分别求取了原式的上界和下界， 分别对应的提出了EVD-LB 和 EVD-UB算法。同样的， 由于暂时的忽略了恒模约束， 在求解完成后也需要一步相位提取操作， 这也造成了算法并非严谨收敛。 这里懒得一个个详述了， paper里有详细的推导。

仿真性能

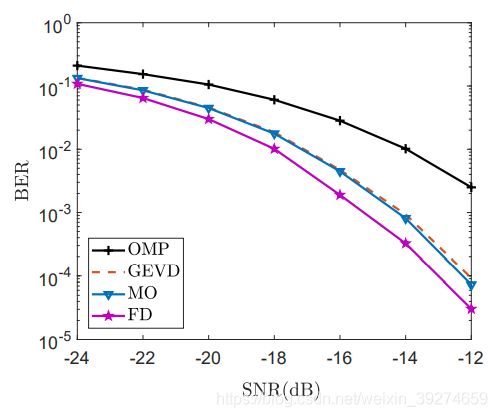
窄带情形

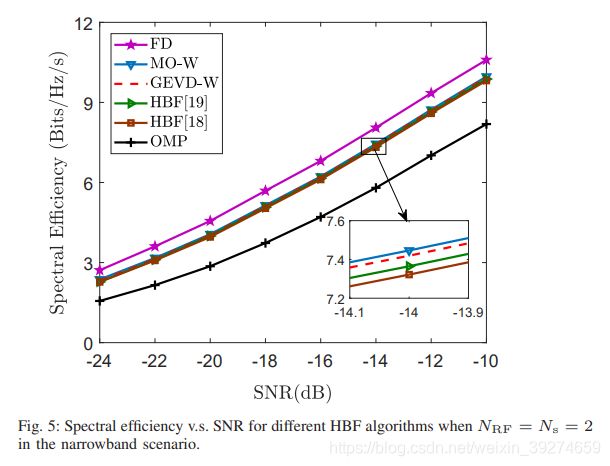
宽带情形

总结

相比于其他相关的工作， 本文提出的算法不仅在BER上有显著的飞跃， 在Rate性能上也有不错的提升。这同时也说明了， 除了以最主流的Rate指标为优化目标外， MSE也是一个可以考虑的准则。