图的常见算法实现(汇总)
前言
本来是想用C语言好好写的,可是指针和结构体太烦人了,弄得我头凉。因此决定用python实现一下图的一些算法。
远程仓库地址:
https://github.com/XiaoZhong233/DataStructure_Python/tree/master/graph
图的存储结构实现
图的实现有邻接矩阵,邻接表,十字链表等。我后面的算法主要用邻接表
建议直接看
[邻接表实现2,基于字典实现](# 邻接表实现2 (基于字典实现,好用))
首先定义了一个异常类:
class GraphError(Exception):
pass
邻接矩阵实现
基于邻接矩阵定义了一个实现图的类,其中矩阵元素可以是1或者其他权值,表示有边,或者用一个特殊值表示“无关联”。构造参数的unconn就是表示无关联的值,默认为0。
图的构造函数的主要参数是mat,表示初始的邻接矩阵。要求是一个二维数组,且为方阵。代码如下
# unconn 无关联参数
# 邻接矩阵实现
class Graph:
def __init__(self, mat, unconn=0):
vnum = len(mat)
# 检查是否为方阵
for x in mat:
if len(x) != vnum:
raise ValueError("参数错误:不为方阵")
# 拷贝数据
self._mat = [mat[i][:] for i in range(vnum)]
self._unconn = unconn
self._vnum = vnum
# 返回顶点数目
def vertex_num(self):
return self._vnum
# 检查该顶点是否合法,也就是下标是否找得到
def _invalid(self, v):
return v < 0 or v >= self._vnum
# 加入新的顶点
def add_vertex(self):
raise GraphError("邻接矩阵不支持加入顶点")
# 加入新的边
def add_edge(self, vi, vj, val=1):
if self._invalid(vi) or self._invalid(vj):
raise GraphError("顶点不合法")
self._mat[vi][vj] = val
# 获得某条边
def get_edge(self, vi, vj):
if self._invalid(vi) or self._invalid(vj):
raise GraphError("顶点不合法")
return self._mat[vi][vj]
# 获得某个顶点的出边
def out_edges(self, vi):
if self._invalid(vi):
raise GraphError("顶点不合法")
return self.out_edge(self._mat[vi], self._unconn)
# 获得某个顶点的出边
@staticmethod
def _out_edges(row, unconn):
edges = []
for i in range(len(row)):
if row[i] != unconn:
edges.append((i, row[i]))
return edges
def __str__(self):
return "[\n" + ",\n".join(map(str, self._mat)) + "\n]" \
+ "\nUnconnected: " + str(self._unconn)
这个简单的邻接矩阵实现的图类并未支持增加顶点,因为邻接矩阵增加顶点要增加多一行一列,挺麻烦的,就不想写了。
邻接表实现1(基于邻接矩阵,不好用)
邻接矩阵的缺点是占用空间很多,如果是稀疏图就很难受了,可能会有很大的空间损失,因此常用邻接表实现图的存储。在上面邻接矩阵的实现下,可考虑一种“压缩后”的邻接表实现。
# 邻接表实现(压缩邻接矩阵形式)
class GraphAL(Graph):
def __init__(self, mat=[], unconn=0):
vnum = len(mat)
for x in mat:
if len(x) != vnum:
raise ValueError("参数错误:不为方阵")
self._mat = [Graph._out_edges(mat[i], unconn) for i in range(vnum)]
self._vnum = vnum
self._unconn = unconn
def add_vertex(self):
self._mat.append([])
self._vnum += 1
return self._vnum - 1
def add_edge(self, vi, vj, val=1):
if self._vnum == 0:
raise GraphError("无法为空图增加边")
if self._invalid(vi) or self._invalid(vj):
raise GraphError("顶点不合法")
row = self._mat[vi]
i = 0
while i < len(row):
if row[i][0] == vj:
self._mat[vi][i] = (vj, val)
return
if row[i][0] > vj: # 没有到与vj的边,退出循环加入边
break
i += 1
self._mat[vi].insert(i, (vj, val))
def get_edge(self, vi, vj):
if self._invalid(vi) or self._invalid(vj):
raise GraphError("顶点不合法")
for i, val in self._mat[vi]:
if i == vj:
return val
return self._unconn
def out_edges(self, vi):
if self._invalid(vi):
raise GraphError("顶点不合法")
return self._mat[vi]
邻接表实现2 (基于字典实现,后面的算法都以此作为存储结构)
新建一个GraphAL.py文件,在文件中添加:
# 邻接表实现无向网(图)(字典形式)
class GraphAL:
def __init__(self, graph={}):
self._graph = graph
self._vnum = len(graph)
def _invalid(self, vertex):
return self._graph.__contains__(vertex)
def add_vertex(self, vertex):
if self._invalid(vertex):
raise GraphError("添加顶点失败,已经有该顶点")
self._graph[vertex] = {}
self._vnum += 1
def add_edge(self, vi, vj, val):
if not self._invalid(vi) or not self._invalid(vj):
raise GraphError("不存在" + vi + "或者" + vj + "这样的顶点")
self._graph[vi].update({vj: val})
self._graph[vj].update({vi: val})
def get_edge(self, vi, vj):
if not self._invalid(vi) or not self._invalid(vj):
raise GraphError("不存在" + vi + "或者" + vj + "这样的顶点")
return self._graph[vi][vj]
def get_vertexNum(self):
return self._graph.__len__()
# 在无向网(图)中是边,有向网(图)是出边,取决于数据
def out_edge(self, vertex):
if not self._invalid(vertex):
raise GraphError("不存在" + vertex + "这样的顶点")
return self._graph[vertex]
你也可以不传入图的参数,会默认创建一个新图。通过add_vertex和add_edge即可完成图的构建。
数据格式如下所示:
graph = {
"A": {"B": 5, "C": 1},
"B": {"A": 5, "C": 2, "D": 1},
"C": {"A": 1, "B": 2, "D": 4, "E": 8},
"D": {"B": 1, "C": 4, "E": 3, "F": 6},
"E": {"C": 8, "D": 3},
"F": {"D": 6},
}
如上图所示,该类是一个无向网,如果需要改成有向网,只需要更改add_edge这个方法,修改为:
def add_edge(self, vi, vj, val):
if not self._invalid(vi) or not self._invalid(vj):
raise GraphError("不存在" + vi + "或者" + vj + "这样的顶点")
self._graph[vi].update({vj: val})
图的一些算法实现
图的遍历
BFS(广度优先搜索)
算法原理及步骤
按照广度优先原则遍历图,利用了队列,有点像树的层次遍历。广度优先遍历的结果不唯一。整个遍历过程大概是这样的:给定一个起始顶点,将该起始顶点入队
- 顶点出队,如果当前顶点未被标记访问,则访问该顶点,然后标记为已访问,如果当前顶点已访问则直接丢弃该顶点
- 当前访问顶点的邻接顶点入队
- 当队列不为空的时候,循环1,2步
算法流程
算法实现
# 广度优先遍历
def bfs(self, start):
if not self._invalid(start):
raise GraphError("不存在" + start + "这样的顶点")
queue = [start] # 队列实现BFS
seen = set(start) # 记录访问过的顶点
parent = {start: None} # Node代表根节点,数组形式保存树
result = []
while queue.__len__() > 0: # 队非空时
vertex = queue.pop(0) # 队首顶点出队
nodes = self._graph[vertex] # 获得其邻接顶点
for node in nodes:
if node not in seen:
queue.append(node) # 其邻接顶点如果没有被访问,则入队,并且保留父顶点
seen.add(node)
parent[node] = vertex
result.append(vertex)
return result, parent
测试
例如遍历下图
具体的存储结构为:
data = {
"A": {"B": 5, "C": 1},
"B": {"A": 5, "C": 2, "D": 1},
"C": {"A": 1, "B": 2, "D": 4, "E": 8},
"D": {"B": 1, "C": 4, "E": 3, "F": 6},
"E": {"C": 8, "D": 3},
"F": {"D": 6},
}
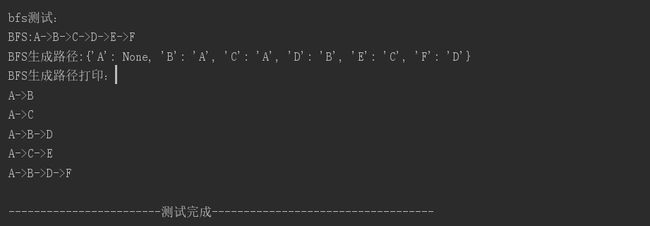
def test_bfs(self):
print("bfs测试:")
bfs, bfsparent = TestGraph.g.bfs("A")
print("BFS:" + graph.GraphAL.printPath(bfs))
print("BFS生成路径:" + bfsparent.__str__())
print("BFS生成路径打印:" + graph.GraphAL.printTreePath(bfsparent).__str__())
pass
DFS(深度优先搜索)
算法原理及步骤
DFS和BFS很像,不过DFS是深度优先的原则,具体实现是栈。
DFS遍历的结果不唯一。整个遍历过程大概是这样的:给定一个起始顶点,将该起始顶点入栈
- 顶点出栈,如果当前顶点未被标记访问,则访问该顶点,然后标记为已访问,如果当前顶点已访问则直接丢弃该顶点
- 当前访问顶点的邻接顶点入栈
- 当栈不为空的时候,循环1,2步
算法流程
算法实现
# 深度优先遍历
def dfs(self, start):
if not self._invalid(start):
raise GraphError("不存在" + start + "这样的顶点")
stack = [start] # 栈实现DFS
seen = set(start) # 记录访问过的顶点
parent = {start: None} # Node代表根节点,数组形式保存树
result = []
while stack.__len__() > 0: # 栈非空时
vertex = stack.pop() # 顶点出栈
nodes = self._graph[vertex] # 获取出栈顶点的邻接顶点
for node in nodes:
if node not in seen:
stack.append(node)
seen.add(node)
parent[node] = vertex
result.append(vertex)
return result, parent
测试
例如遍历下图
存储结构
data = {
"A": {"B": 5, "C": 1},
"B": {"A": 5, "C": 2, "D": 1},
"C": {"A": 1, "B": 2, "D": 4, "E": 8},
"D": {"B": 1, "C": 4, "E": 3, "F": 6},
"E": {"C": 8, "D": 3},
"F": {"D": 6},
}
测试结果
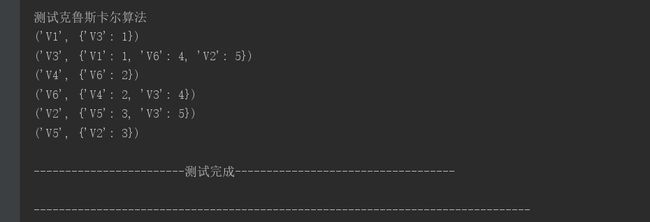
图的结构为:
('A', {'B': 5, 'C': 1})
('B', {'A': 5, 'C': 2, 'D': 1})
('C', {'A': 1, 'B': 2, 'D': 4, 'E': 8})
('D', {'B': 1, 'C': 4, 'E': 3, 'F': 6})
('E', {'C': 8, 'D': 3})
('F', {'D': 6})
dfs测试:
DFS:A->C->E->D->F->B
DFS生成路径:{'A': None, 'B': 'A', 'C': 'A', 'D': 'C', 'E': 'C', 'F': 'D'}
DFS生成路径打印:
A->B
A->C
A->C->D
A->C->E
A->C->D->F
最小生成树
最小生成树针对的是连通网而言的。假定一个网络G,他的边带有权值,自然可以通过BFS,DFS获得他的生成树,权值最小的那棵树,就称最小生成树
最小生成树有许多实际的应用,例如通信网,输电网及各种网的规划。
Prim算法
算法原理及算法流程
原理:
根据(MST性质:网络G必有一颗最小生成树),具体证明不再赘述,大概思想就是假设你现有一个图的集合G,从G中的一个顶点出发,不断的选择最短的一条连接边,扩充到已选边集N中,直至N包含了图G中的所有顶点。
构造过程举例
假设现在有这样一颗图
要对该图进行prim算法进行最小生成树。首先找一个开始顶点,假设从V1开始
第一次构造
V1的邻接节点全部入队。并且由于该队列是优先级队列,会按照权重排序
队首出队,构造边,将该边加入到N集
此时N集中就有了一条边了
V3除了N集中的结点的邻接节点入队,优先队列会按照权重进行排序
第二次构造
队首出队,构造边,将该边加入到N集
此时N集有两条边了
将V6的除N集中已有的邻接节点入队,
第三次构造
队首出队,构造边,将该边<6,4>加入到N集
此时的N集就有三条边了
将V4的除N集中已有的邻接节点入队,发现v4的邻接顶点都在N集中了,所以没有顶点入队
第四次构造
队首
所以,当前N集中的边还是和原来一样,如下图:
将V4的除N集中已有的邻接节点入队,发现v4的邻接顶点都在N集中了,所以没有顶点入队
第五次构造
队首
此时N集就有五条边了
将V2的除N集中已有的邻接节点入队
第六次构造
队首
最终结果
算法实现
# prim算法,最小生成树,前提该图必须是连通网
def prim(self, start):
if not self._invalid(start):
raise GraphError("不存在" + start + "这样的顶点")
result = GraphAL({})
edgeCount = 0
pqueue = [] # 优先级队列,候选列表
# 初始化优先级队列
for node in self._graph[start]:
heapq.heappush(pqueue, (self._graph[start][node], start, node))
pass
while edgeCount < self.get_vertexNum() - 1 and not pqueue.__len__() == 0:
# 出队
pair = heapq.heappop(pqueue)
distance = pair[0]
start = pair[1]
end = pair[2]
# 判断是否有该顶点,如果没有就要加入
if start not in result._graph:
result.add_vertex(start)
if end not in result._graph:
result.add_vertex(end)
# 如果当前点与下一节点未建立边,则尝试建立边
# 方式是检查下一节点是否在result中,如果有则说明这个节点已经建立过边了,再建立边的话会可能会形成连通,因此直接舍弃该边的建立
if end not in result._graph[start]:
# 如果下一个节点如果未被其他节点连接则result._graph[end]返回false,开始构造边,
# 如果下一个节点已经被连接了,则result._graph[end]返回true,舍弃该边的建立
if not result._graph[end]:
result.add_edge(start, end, distance)
edgeCount += 1
pass
start = end
# 子节点入队
for node in self._graph[start]:
if node not in result._graph:
heapq.heappush(pqueue, (self._graph[start][node], start, node))
pass
return result
测试
与刚才流程构造的结果一致
克鲁斯卡尔算法
算法原理及流程
原理
在一个连通图中不断选取权值最小的边,然后连起来,就是这样。
假设给定图G,结果图T
基本步骤如下:
- 将G中的所有边按权值递增的顺序进行排序
- 选择权值最短的边且边的两端点属于不同连通分量(如果两端点属于同一个连通分量中,那么就说明该子图是连通图!所以不行),然后该边与T中已选择的边进行连接,每次边连接都会使得T的连通分量减1
- 当边数小于顶点数时,不断重复1,2
如果当做完上面这些步骤后,得出的结果T中不能包含G中的所有顶点,则说明原图G是不连通的(也就是不是任意一个节点到另一个节点都走的通)
这里有两个难点:
-
最短边的选取
思路①:采用优先队列,在python中可以通过优先级队列实现,其他语言像C++,Java中也有类似实现的数据结构。
思路②:不断的扫描候选边列表,然后进行排序。这种方法就比较麻烦了,写的代码比较多,不过也很灵活,具体排序方式你可以选择。
-
如何判断边的两个端点的连通分量
思路①:不断的检查两个端点之间是否有路径,有路径就说明在同一个子图中,连通分量相同。不过这样也太麻烦了点还浪费计算时间
思路②:前人提出的一种方法,为每个连通分量确定一个代表元,如果两个顶点的代表元相同,则表示他们连通成环。例如下图
v1V2V3V4当初始化的时候
v1,v2,v3,v4的代表元就是他们的序号也就对应0,1,2,3当
v1v2构成新边的时候,就要把v2的代表元改为v1的代表元0。这时候
v1,v2,v3,v4的代表元就更新为0,0,2,3v1V2V3V4v1v2是的连通分量相同并且他们的代表元也是相同的。类似,如果想要连接
v2v3,此时v2v3的代表元不同,因此连接了也不会构成环。 直接把v3的代表元修改为v2的代表元即可,即0v1V2V3V4此时
v1v2v3是连通的,他们的代表元是0,0,0如果下一次操作中,想要把
v3连接到v1,检查他们的代表元,都是0所以连接起来一定会构成环v1V2V3V4因此,可以使用代表元判断欲加入的边是否会与已选择集合T中的边构成环路。
构成过程举例
假设还是之前的这颗图G,其结果集T中目前还为空
初始化
全部边入队,自动在优先队列中根据权值排好序
并且初始化代表元列表,初始值为他们的下标。
例如v1的代表元初始值为1,v2的代表元初始值为2…vn的代表元初始值为n
第一次构造
- 队首出队,所以
- 检查
v1v3的代表元,很明显不同,所以将
- 合并代表元,修改等于代表元值为3的代表元的值,改为
v1的代表元即1
第二次构造
- 队首出队,所以
- 检查
v4v6的代表元,很明显不同,所以将
- 合并代表元,修改等于代表元值为6的代表元的值,改为
v4的代表元的值即4
第三次构造
- 队首出队,所以
- 检查
v2v5的代表元,很明显不同,所以将
- 合并代表元,修改等于代表元值为5的代表元的值,改为
v2的代表元的值即2
第三次构造
- 队首
- 检查
v3v6的代表元,不同,所以将
- 合并代表元,修改等于代表元值为4的代表元的值,改为
v3代表元的值即1
第四次构造
- 队首
- 检查
v1v4的代表元,相同,所以不将
- 此时代表元不进行任何操作
第五次构造
- 队首
- 检查
v3v4的代表元,相同,所以不将
- 此时代表元不进行任何操作
第六次构造
- 检查
v2v3的代表元,不同,所以将
- 合并代表元,修改等于代表元为2的代表元的值,改为
v3代表元的值即1
可以发现,当前T集合中已经有5条边了,最小生成树已经生成完毕。同时观察到,代表元中的值也相同了,表示他们都在同一个子图中了。
算法实现
# kruskal算法,最小生成树,前提该图必须是连通网
def kruskal(self):
# 初始化代表元和结果图
result, reps, pqueue, edgesCount = GraphAL(graph={}), {}, [], 0
for key in self._graph.keys():
reps[key] = key
# 边入队,按优先级排序,选出最短边
for key in self._graph:
for end in self._graph[key].keys():
edges = self._graph[key][end]
heapq.heappush(pqueue, (edges, key, end)) # 边入队
pass
# 当边数达到n-1条时,即成功得到最小生成树时停止
while edgesCount < self.get_vertexNum() - 1 and not pqueue.__len__() == 0:
# 出队
pair = list(heapq.heappop(pqueue))
# 判断是否有该顶点,如果没有就要加入
if pair[1] not in result._graph:
result.add_vertex(pair[1])
if pair[2] not in result._graph:
result.add_vertex(pair[2])
# 检查两点是否属于不同连通分量
if reps[pair[1]] != reps[pair[2]]:
result.add_edge(pair[1], pair[2], pair[0])
edgesCount += 1
# 合并连通分量
rep, orep = reps[pair[1]], reps[pair[2]]
for key in reps.keys():
if reps[key] == orep:
reps[key] = rep
return result
pass
测试
与刚才结果自动推的完全一致。
最短路径
dijkstra算法
算法原理
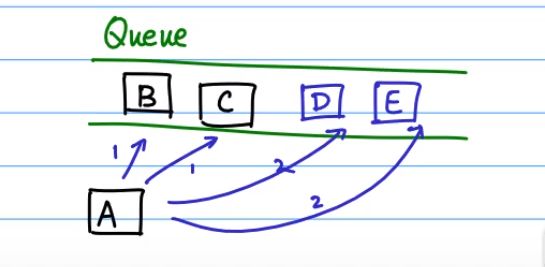
在看迪杰斯特拉算法之前,可以先回顾下BFS算法的过程。BFS的实现是通过一个队列实现。还是这张图
选择假设BFS从A节点开始,A节点出队后,将A的邻接节点B,C入队
然后B出队,D入队,C出队,E入队。整个BFS的流程大概如此,在这之中,可以看到BFS队列中不同节点离A的距离,每个出队的结点对于他的邻接节点的距离都是1,并且在队列中他们也是紧紧挨着的。
假如可以把这些顶点进行排序,然后不断更新队中节点到A的距离值,那么应该可以一步步的获得当前节点到A节点的最短距离了。
该算法有两个难点:
- 如何排序
我使用的是python的优先队列,该队列是基于堆这一种数据结构实现的,你也可以自行选择排序算法进行排序
- 如何更新距离
在BFS中每个节点到A的距离是固定的,是不会发生更新操作的,这是由于BFS算法实现过程中有个访问标志会标志某个节点是否已被访问,该标志保证了每个节点只访问一次。但是在迪杰斯特拉算法中,这样是不行的,因为想要在每个节点出队后,都要将该结点的邻接节点到目标点(这个例子中是A点)的距离进行比较更新,选择权值和小的。
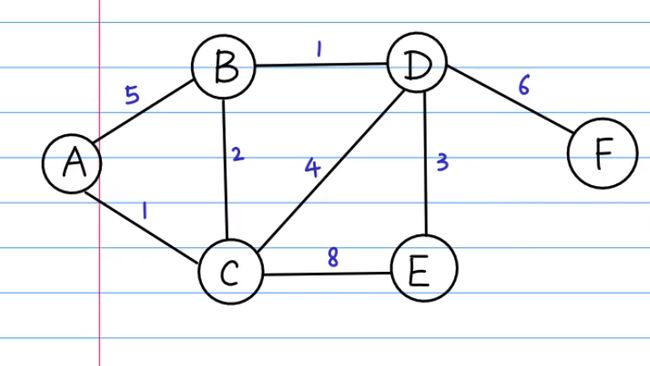
看下面这个网
当遍历到B的时候A到B有两条路,一条是A-B,另一条是A-C-B,前者的距离为5,比较长,后者的距离为3(1+2)。在迪杰斯特拉中就会选择路径A-C-B这条路径。
在实际的算法实现中,距离的比较是通过一个distance的列表实现的,该列表距离了每个顶点到目标点的最短距离。然后在下一次遍历中不断得更新这个距离就可以了。
构造过程举例
假设还是上面这个图。
要求图中顶点到A的最短距离
初始化
初始化距离列表,inf 表示无穷,A的目标点,所以距离为0
初始化优先级队列,目标节点A入队
当队列不为空时,循环。
第一次构造
- A出队,并标记为已访问,遍历A的邻接节点B、C,同时将A到B的距离5(0+5)和A到C的距离1(0+1),与
distance列表中的距离进行比较,由于distance中的距离都是无穷,所以distance中C的距离更新为1,B的距离更新为5
- B,C节点由于距离被更新了。需要参与下一次比较,所以B、C入队
第二次构造
- C出队,并标记为已访问,遍历C的邻接节点A,B,D,E,将C-A的距离1,C-B的距离3(1+2)和C-D的距离5(1+4)和C-E的距离9(1+8),与
distance列表中的B,C,E的距离进行比较,更新为其中的较小值
- 由于B,D,E的距离被更新了。需要参与下一次的比较,所以B,C,E需要入队,带着他们的更新后的权值
第三次构造
- B出队,并标记为已访问,遍历B的子节点D,C,A,将B-D(3+1=4),B-C(3+2=5),B-A(3+5)的距离分别与
distance中的D,C,A距离进行比较,取小的值,发现只有D的距离被更新为了4
- 由于D被更新了,需要参与下一次的比较,所以D入队,带着D更新后的权值
第四次构造
- D出队,并标记为已访问,遍历D的子节点B,C,E,F。将D-B(4+1=5),D-C(4+4=8),D-E(4+3=7),D-F(4+6=10)的距离分别与
distance中的B,C,E,F距离进行比较,取小的值
- 由于只有E,F的距离被更新为7,和10,所以E,F需要带着他们更新后的权值入队,参与下一次的比较。
第五次构造
- 队首B出队,由于B被标记已访问,所以直接扔掉,进入下一个循环
- 队首D出队,由于D已经被标记已访问,扔掉。进入下一个循环
-
队首E出队,标记为已访问。遍历其邻接节点C,D,将E-C(7+4=11),E-D(7+3=10)与
distance中的C,D值进行比较,取小的值,发现C,D都不需要更新。 -
由于没有节点被更新,所以没有节点入队。此时的
distance如下图
第六次构造
- 队首E出队,由于E被标记为已访问,扔掉,进入下一个循环
- 队首E出队,由于E被标记为已访问,扔掉,进入下一个循环
- 队首F出队,发现他没有子节点,所以
distance不会被更新,队列将不会加入新的结点。此时的distance如下图
第七次构造
由于此时队列为空,所以循环结束,迪杰斯特拉算法求解完毕!此时的distance就是每个节点到目标点A的最短距离了。
迪杰斯特拉算法就是基于这种"宽度优先遍历"的思想,按路径的长度选择下一个最短节点然后逐步扩张(这一点也很像用MST性质实现的prim算法)。这个算法在探索中也会更新已经节点的最短路径,每一步都可以找到一个确定的最短路径,这就是典型的动态规划思想(在计算中保留一些信息,用来支持下一步的决策信息)
算法实现
# 迪杰斯特拉法算最短路径
def dijkstra(self, start):
if not self._invalid(start):
raise GraphError("不存在" + start + "这样的顶点")
graph = self._graph
pqueue = [] # 优先级队列
heapq.heappush(pqueue, (0, start)) # 根顶点进队,最高优先级
seen = set() # 记录访问过的顶点
parent = {start: None} # 生成树
distance = self.__init_distance(start) # 初始化距离
while pqueue.__len__() > 0:
pair = heapq.heappop(pqueue) # pop弹出的是元组,第一个参数是距离(优先级),第二个是顶点
dist = pair[0]
vertex = pair[1]
seen.add(vertex) # 记录访问过的顶点
nodes = graph[vertex].keys() # 获取其顶点的邻接顶点
for node in nodes:
if node not in seen:
if dist + graph[vertex][node] < distance[node]: # 如果当前顶点到开始顶点的距离小于距离列表中的值,更新距离
heapq.heappush(pqueue, (dist + graph[vertex][node], node))
parent[node] = vertex
distance[node] = dist + graph[vertex][node]
# 输出遍历结果
# print(vertex)
return distance, parent
pass
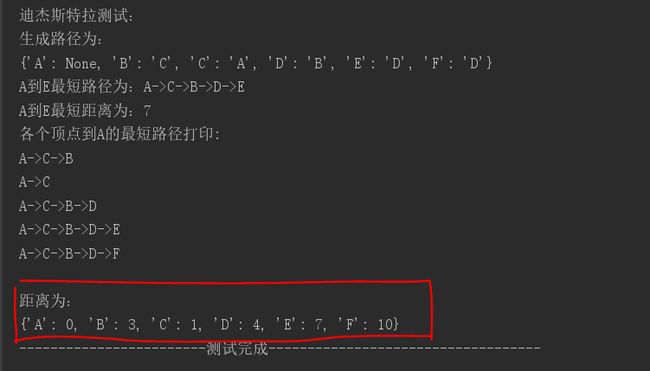
测试
可以发现,如刚才推导的结果一模一样。
弗洛依德算法(待填坑)
算法原理
算法实现
测试
拓扑排序
算法原理
拓扑排序是有向图(网)中的内容,只在有向网(图)的范畴中讨论。
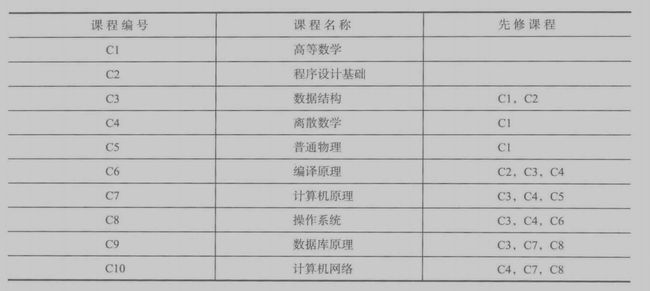
先看一个实际生活中可能遇到的问题:选课问题,例如上大一的时候你肯定要先学C语言,然后才能学数据结构。这个时候C语言和数据结构就构成了一个排列问题,谁在前谁在后。用图中的顶点表示一个活动,边表示活动之间的顺序关系。这样的图就称为AOV网(顶点活动网)
下图就是一个典型的AOV网实例。
任何无回路的AOV网N都可以求解出拓扑序列,方法很简单:
- 从N中选出一个入度为0的顶点作为序列的下一个顶点
- 从N网中删除所选顶点的出边
- 重复执行上面两步,直到已经选出了图N的所有顶点
拓扑排序算法有两个难点:
- 如何寻找入度为0的顶点
- 真的需要拷贝整张图,然后进行删除
一个显然的办法是不断遍历图,寻找入度为0的顶点。但时间代价会很高。顶点间的制约关系决定了顶点的入度。入度是一个整数,用一个整数表就能记录所以顶点的入度了。因此,我的方法是用一张入度表记录了每个顶点的入度,初始时,表中的各顶点的入度对应为图中顶点的入度,在随后的计算中,一旦选中一个顶点,就将该顶点的出边入度减一。
在实际的算法实现中还用了一个0度栈来记录已经入度为0但还未处理的顶点。
算法比较简单。
可以慢慢调试
算法实现
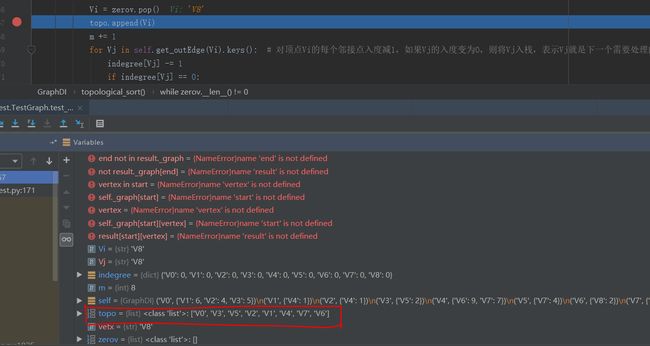
def topological_sort(self):
indegree = {} # 入度表
zerov = [] # 利用0度栈记录已知的入度为0的但还未处理的顶点
m = 0 # 输出顶点计数
topo = [] # 拓扑排序结果
# 生成入度表和0度栈
for vetx in self._graph:
indegree[vetx] = self.get_inEdge(vetx).__len__()
if indegree[vetx] == 0:
zerov.append(vetx)
pass
while zerov.__len__() != 0:
Vi = zerov.pop()
topo.append(Vi)
m += 1
for Vj in self.get_outEdge(Vi).keys(): # 对顶点Vi的每个邻接点入度减1,如果Vj的入度变为0,则将Vj入栈,表示Vj就是下一个需要处理的顶点
indegree[Vj] -= 1
if indegree[Vj] == 0:
zerov.append(Vj)
if m < self.get_vertexNum(): # 该有向图有回路
return False
return topo
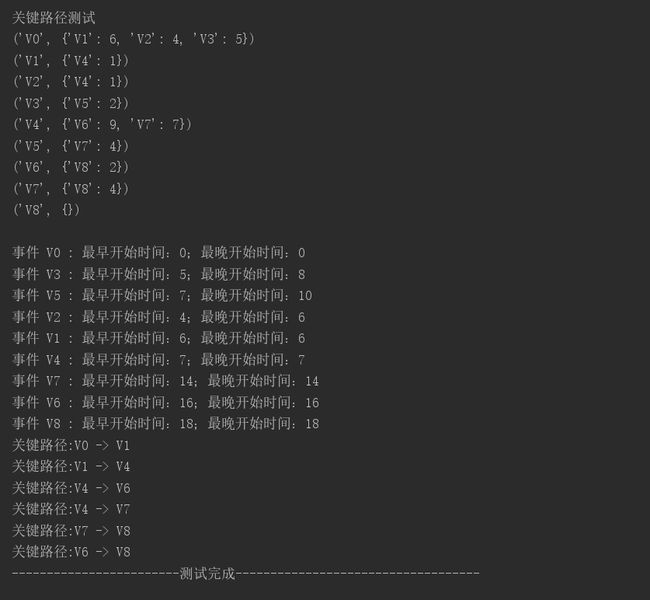
测试
关键路径
算法原理
算法实现
# 关键路径
def criticalPath(self, delay=0):
topo = self.topological_sort()
if not topo:
raise GraphError("存在有向环!")
ve = [0 for i in range(len(topo))] # 事件最早开始时间
vl = [0 for i in range(len(topo))] # 事件最迟开始时间
cp = [] # 关键路径
result = {} # 返回结果
# --------------------------------计算事件的最早发生时间-----------------------------
for i in range(topo.__len__()):
start = topo[i] # 取出拓扑节点
for node in self.get_outEdge(start).keys(): # 获取拓扑节点的邻接点,计算ve
w = self._graph[start][node] # 当前节点与邻接节点的边
j = topo.index(node) # 邻接节点的下标
if ve[j] < ve[i] + w: # 更新邻接点的最早发生时间,选大的时间
ve[j] = ve[i] + w
pass
# --------------------------------计算事件的最晚发生时间-----------------------------
for i in range(topo.__len__()): # 给每个事件的最迟发生时间置初值,初值为最早发生时间中的最大值
vl[i] = ve[topo.__len__() - 1] + delay
for i in reversed(range(topo.__len__())):
k = topo[i] # 取出拓扑节点
for node in self.get_inEdge(k).keys(): # 获取拓扑节点的逆邻接点,计算vl
w = self._graph[node][k] # 逆邻接点和当前节点的边
j = topo.index(node) # 逆邻接点的下标
if vl[j] > vl[i] - w: # 更新逆邻接点的最晚发生时间,选小的时间
vl[j] = vl[i] - w
pass
# --------------------------------判断每一活动是否为关键路径--------------------------
for i in range(topo.__len__()):
start = topo[i]
for node in self.get_outEdge(start).keys():
j = topo.index(node) # 获得邻接顶点的下标
w = self._graph[start][node] # 当前节点与邻接节点的边
e = ve[i] # 计算活动的最早开始时间
l = vl[j] - w - delay # 计算活动的最晚开始时间
if e == l:
cp.append((start, node)) # 如果相等就说明为关键路径
pass
for i in range(topo.__len__()):
result[topo[i]] = (ve[i], vl[i])
pass
return result, cp