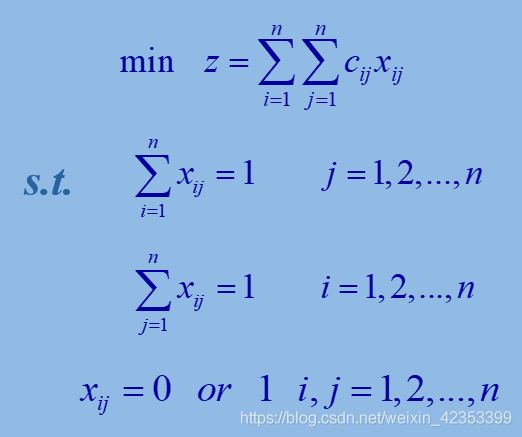python的scipy（匈牙利算法）解决教学任务指派问题

参考资料：
匈牙利算法求解教学任务指派问题
指派问题
组合优化理论里的第六章_指派问题的课件

问题简介

在生活中经常遇到这样的问题，某单位需完成n项任务，恰好有n个人可承担这些任务。由于每人的专长不同，各人完成任务不同(或所费时间)，效率也不同。于是产生应指派哪个人去完成哪项任务，使完成n项任务的总效率最高(或所需总时间最小)。这类问题称为指派问题或分派问题。
教学任务指派问题为指派问题中的一种，考虑教师对课程的擅长程度，教学任务饱满序列和学生对教师的满意度，通过匈牙利算法求得最优课程指派。

算法

指派问题一般模型：

匈牙利算法：

教师与课程一样多

把求最大值变为求最小值问题：矩阵C=20-擅长矩阵。
再进行匈牙利算法操作：


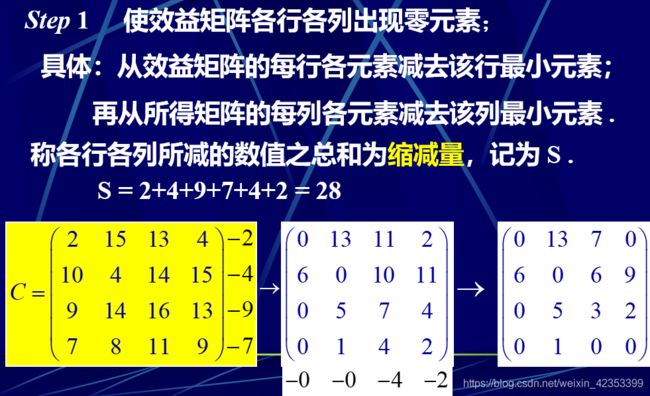
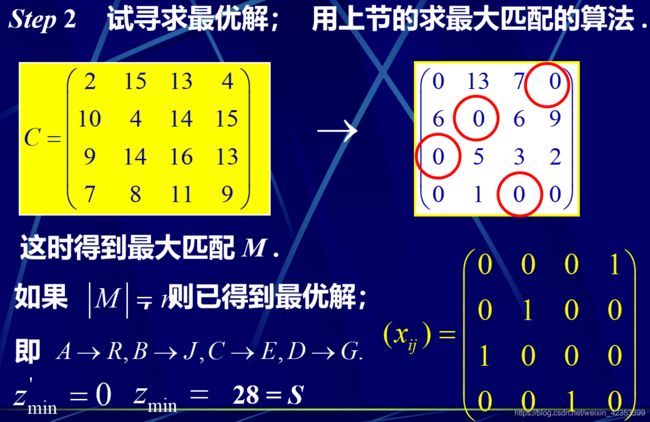
如果得不到解，则：


程序实现：

#教学任务指派问题
import numpy as np
from scipy.optimize import linear_sum_assignment

def printf(row_ind,col_ind):#输出
    print("最优教师课程指派：")
    for i in range(len(row_ind)):
        print("教师",row_ind[i],"->课程",col_ind[i],end='; ')
    print()
#教师与课程一样多
#各个教师对各个课的擅长程度矩阵
goodAt =np.array([[18,5,7,16],[10,16,6,5],[11,6,4,7],[13,12,9,11]])
weakAt=20-goodAt
row_ind,col_ind=linear_sum_assignment(weakAt)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(goodAt[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素，形成数组
print(goodAt[row_ind,col_ind].sum())#数组求和
printf(row_ind,col_ind)

输出结果：

教师少与课程多

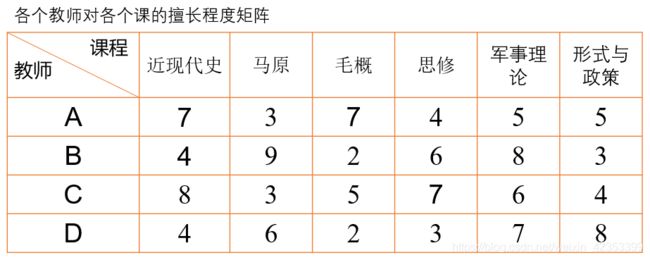
把求最大值变为求最小值问题：矩阵C=10-擅长矩阵。
设想每个教师都有个分身，问题变为8个教师完成6项教学任务，虚设两门课程，擅长程度都为最大值。
得到矩阵C为：

程序实现：

#当教师少课程多
#各个教师对各个课的擅长程度矩阵
goodAt =np.array([[7, 3, 7, 4, 5, 5],[7, 3, 7, 4, 5, 5],
       [4, 9, 2, 6, 8, 3],[4, 9, 2, 6, 8, 3],
       [8, 3, 5, 7, 6, 4],[8, 3, 5, 7, 6, 4],
       [4, 6, 2, 3, 7, 8],[4, 6, 2, 3, 7, 8]])
weakAt=10-goodAt
row_ind,col_ind=linear_sum_assignment(weakAt)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(goodAt[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素，形成数组
print(goodAt[row_ind,col_ind].sum())#数组求和
printf(row_ind,col_ind)

输出结果：

结果表明：教师A教课程2；教师B教课程1和课程4；教师C教课程0和课程3；教师D教课程5.

教师少与课程多且一个教师最多教两门课，最少一门

把求最大值变为求最小值问题：矩阵C=10-擅长矩阵。
设想每个教师都有个分身，问题变为8个教师完成6项教学任务，虚设两门课程，擅长程度一个为最大值，另一个为最小值。
得到矩阵C为：

程序实现：

#教师少课程多且一个教师最多教两门课，最少一门
goodAt =np.array([[7,3,7,4,5,5,0,0],[7,3,7,4,5,5,100,100],
                [4, 9, 2, 6, 8, 3,0,0],[4, 9, 2, 6, 8, 3,100,100],
                [8, 3, 5, 7, 6, 4,0,0],[8, 3, 5, 7, 6, 4,100,100],
                [4, 6, 2, 3, 7, 8,0,0],[4, 6, 2, 3, 7, 8,100,100]])
weakAt=100-goodAt
row_ind,col_ind=linear_sum_assignment(weakAt)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(goodAt[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素，形成数组
print(goodAt[row_ind,col_ind].sum())#数组求和
printf(row_ind,col_ind)

输出结果：

课程6，7不存在，虚设的。
结果表明：教师A教课程2；教师B教课程1和课程4；教师C教课程0和课程3；教师D教课程5.

实际问题

（参照《匈牙利算法求解教学任务指派问题》）
某高校计划开设创客空间，需要开展的教学任务有焊接、车工、钳铣磨工、数控、3D打印、切割。现有8名教师可承担相关课程教学，教师对教学课程的擅长矩阵G已知。根据救师自身安排、专家组打分和课时等分析，得到教师教学任务的饱满程度序列U。通过问卷调查、往届课程成绩、学生座谈等形式，得到学生对教师的满意 度序列S。请问如何如何安排教师教授的课程？


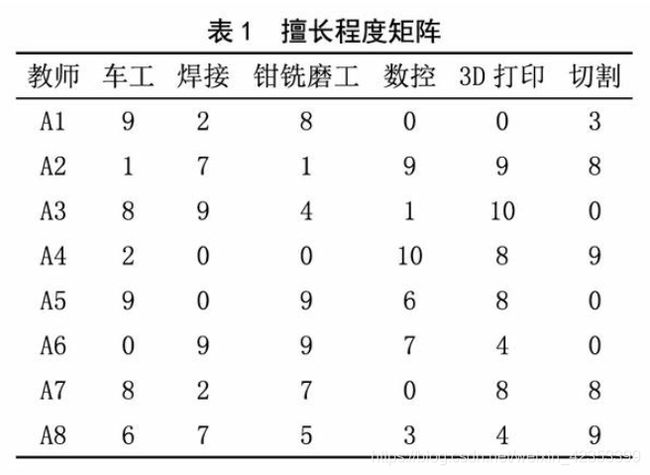
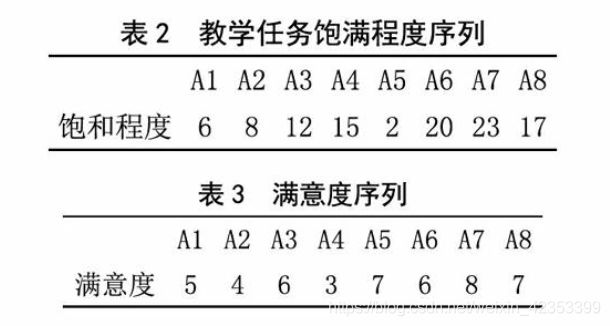
由于该问题涉及因素较多，因此，采用解析方法或传统的匈牙利算法难以给出合适结果。总体最优化的前提是教师擅长课程、精力和学生满意度满足基本要求，木文用比值的方式求解三种因素的综合表现。
首先归一化擅长矩阵G，$G_{ij}$ 值越高，表明第i名教师对第j门课程的握长程度越好。序列U和S经过归一化处理后，也可表现为百分比形式，$U_i$值越高，表明第i名教师的教学任务越饱满；$S_i$值越高，表明学生对第i名教师的满意度越高。以$T_{ij}$表现三种因素综合影响下第i名教师教授第j门课程的情况。$T_{ij}$与$G_{ij}、S_i$呈正相关关系，而与$U_i$呈现负相关关系，计算得到：
$$T_{ij}=\frac{G_{ij}{S}_i}{U_i}$$
模型的目标方程为：
$$maxZ=\sum _{i=1}^n\sum _{j=1}^m{T}_{ij}{X}_{ij}$$

n为教师数量，m为教学课程数量。

程序代码：

import time
start = time.clock()
#教学任务指派问题
import numpy as np
from scipy.optimize import linear_sum_assignment

def printf(row_ind,col_ind):#输出
    print("最优教师课程指派：")
    for i in range(len(row_ind)):
        print("教师",row_ind[i],"->课程",col_ind[i],end='; ')
    print()
#教师少与课程多
#各个教师对各个课的擅长程度矩阵（求max）
goodAt =np.array([[9,2,8,0,0,3],[1,7,1,9,9,8],[8,9,4,1,10,0],[2,0,0,10,8,9],[9,0,9,6,8,0],[0,9,9,7,4,0],[8,2,7,0,8,8],[6,7,5,3,4,9]])
taskfull=np.array([6,8,12,15,2,20,23,17])#教学任务饱和序列
satisfaction=np.array([5,4,6,3,7,6,8,7])#满意度序列
goodAt1=goodAt/goodAt.max()#归一化
taskfull1=taskfull/taskfull.max()
satisfaction1=satisfaction/satisfaction.max()
T=np.zeros(goodAt.shape)#构造综合矩阵
for i in range(len(taskfull)):
    T[i,:]=(goodAt1[i,:]*satisfaction1[i]/taskfull1[i])*10
    
weak=T.max()-T#改为求min
row_ind,col_ind=linear_sum_assignment(weak)
print(row_ind)#开销矩阵对应的行索引
print(col_ind)#对应行索引的最优指派的列索引
print(T[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素，形成数组
print(T[row_ind,col_ind].sum())#数组求和
printf(row_ind,col_ind)

elapsed = (time.clock() - start)
print("Time used:",elapsed)

输出结果：

运行时间与复杂度问题

测试运行时间：

import numpy as np
from scipy.optimize import linear_sum_assignment
import time
start = time.clock()

def printf(row_ind,col_ind):#输出
    print("最优教师课程指派：")
    for i in range(len(row_ind)):
        print("教师",row_ind[i],"->课程",col_ind[i],end='; ')
    print()
#教师与课程一样多
#各个教师对各个课的擅长程度矩阵
goodAt =np.random.randn(500,500)+10
weakAt=goodAt.max()-goodAt
row_ind,col_ind=linear_sum_assignment(weakAt)
#print(row_ind)#开销矩阵对应的行索引
#print(col_ind)#对应行索引的最优指派的列索引
#print(goodAt[row_ind,col_ind])#提取每个行索引的最优指派列索引所在的元素，形成数组
#printf(row_ind,col_ind)
print(goodAt[row_ind,col_ind].sum())#数组求和
elapsed = (time.clock() - start)
print("Time used:",elapsed)