Codeforces Round #228 (Div. 1) B. Fox and Minimal path (构造&最短路)
B. Fox and Minimal path
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
Fox Ciel wants to write a task for a programming contest. The task is: "You are given a simple undirected graph with n vertexes. Each its edge has unit length. You should calculate the number of shortest paths between vertex 1 and vertex 2."
Same with some writers, she wants to make an example with some certain output: for example, her birthday or the number of her boyfriend. Can you help her to make a test case with answer equal exactly to k?
Input
The first line contains a single integer k (1 ≤ k ≤ 109).
Output
You should output a graph G with n vertexes (2 ≤ n ≤ 1000). There must be exactly k shortest paths between vertex 1 and vertex 2 of the graph.
The first line must contain an integer n. Then adjacency matrix G with n rows and n columns must follow. Each element of the matrix must be 'N' or 'Y'. If Gij is 'Y', then graph G has a edge connecting vertex i and vertex j. Consider the graph vertexes are numbered from 1 to n.
The graph must be undirected and simple: Gii = 'N' and Gij = Gji must hold. And there must be at least one path between vertex 1 and vertex 2. It's guaranteed that the answer exists. If there multiple correct answers, you can output any of them.
Examples
input
Copy
2output
Copy
4
NNYY
NNYY
YYNN
YYNNinput
Copy
9output
Copy
8
NNYYYNNN
NNNNNYYY
YNNNNYYY
YNNNNYYY
YNNNNYYY
NYYYYNNN
NYYYYNNN
NYYYYNNNinput
Copy
1output
Copy
2
NY
YNNote
In first example, there are 2 shortest paths: 1-3-2 and 1-4-2.
In second example, there are 9 shortest paths: 1-3-6-2, 1-3-7-2, 1-3-8-2, 1-4-6-2, 1-4-7-2, 1-4-8-2, 1-5-6-2, 1-5-7-2, 1-5-8-2.
题目大意:
输入一个数K,构造一个无向图从1到2有K条最短路,且总点数不超过1000.
解法:
容易知道任意一个数都可以被二进制构造出来,将K拆分成若干个二进制位后,每个二次幂条最短路都可以这样表示:
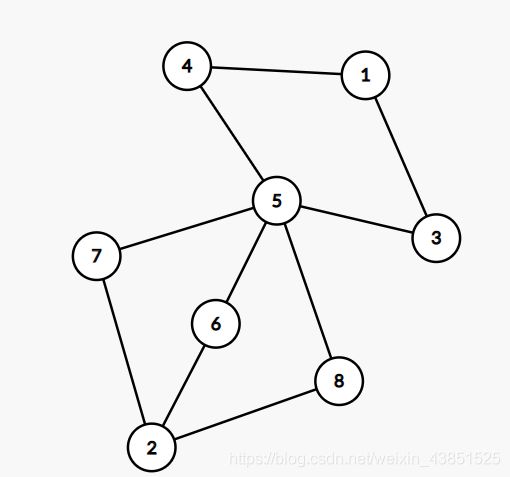
图为K=4的情况,这样每增加一个环,答案就*2,如果这张图的K=6的话,只要从相应二进制位的点往外加一条路径到终点就可以了,像这样:
最短路的长度就等于最大拆分二进制位*2,剩下的二进制位,长度不够直接加点就好啦。
Accepted code
#pragma GCC optimize(3)
#include
#include
using namespace std;
#define sc scanf
#define Min(x, y) x = min(x, y)
#define Max(x, y) x = max(x, y)
#define ALL(x) (x).begin(),(x).end()
#define SZ(x) ((int)(x).size())
#define pir pair
#define MK(x, y) make_pair(x, y)
#define MEM(x, b) memset(x, b, sizeof(x))
#define MPY(x, b) memcpy(x, b, sizeof(x))
#define lowbit(x) ((x) & -(x))
#define P2(x) ((x) * (x))
typedef long long ll;
const int Mod = 1e9 + 7;
const int N = 1e3 + 100;
const int INF = 0x3f3f3f3f;
const ll LINF = 0x3f3f3f3f3f3f3f3f;
inline ll dpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t) % Mod; b >>= 1; t = (t*t) % Mod; }return r; }
inline ll fpow(ll a, ll b){ ll r = 1, t = a; while (b){ if (b & 1)r = (r*t); b >>= 1; t = (t*t); }return r; }
vector ver;
int bit[30]; // 记录相应二进制位的点编号
bool G[N][N];
void Add(int u, int v) {
G[u][v] = G[v][u] = true;
}
int main()
{
int k;
cin >> k;
if (k == 1) {
puts("2"), puts("NY"), puts("YN");
exit(0);
}
else if (k == 2) {
puts("4");
puts("NNYY"), puts("NNYY");
puts("YYNN"), puts("YYNN");
exit(0);
}
else if (k == 3) {
puts("5");
puts("NNYYY"), puts("NNYYY");
puts("YYNNN"), puts("YYNNN");
puts("YYNNN"), exit(0);
} // 特判一些不好处理的情况
int pos = 0; // 拆分二进制位
while (k) {
if (k & 1)
ver.push_back(pos);
k >>= 1;
pos++;
}
int len = ver.back();
int cnt = 2;
int u = cnt; // 初始化最长的
for (int i = 1; i <= len; i++) {
if (i == 1) {
bit[i - 1] = 1;
Add(1, ++cnt), Add(1, ++cnt);
cnt++;
Add(cnt - 1, cnt), Add(cnt - 2, cnt);
u = cnt;
}
else if (i == len) {
bit[i - 1] = u;
Add(u, ++cnt), Add(u, ++cnt);
Add(cnt - 1, 2), Add(cnt, 2);
}
else {
bit[i - 1] = u;
Add(u, ++cnt), Add(u, ++cnt);
cnt++;
Add(cnt - 1, cnt), Add(cnt - 2, cnt);
u = cnt;
}
}
for (int i = 0; i < SZ(ver) - 1; i++) { // 最长以外的二进制位
int u = bit[ver[i]]; // 点编号
int lst = 2 * (len - ver[i]);
for (int j = 1; j <= lst; j++) { // 添加的点数
if (j == lst)
Add(u, 2);
else
Add(u, ++cnt), u = cnt;
}
}
cout << cnt << endl;
for (int i = 1; i <= cnt; i++) {
for (int j = 1; j <= cnt; j++) {
if (G[i][j])
printf("Y");
else
printf("N");
}
puts("");
}
return 0; // 改数组大小!!!用pair记得改宏定义!!!
}